
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




từ điểm B kẻ \(Bz//Cy=>\angle\left(BCy\right)+\angle\left(CBz\right)=180^o\)(góc trong cùng phía)
\(=>\angle\left(CBz\right)=180^o-130^o=50^o\)
\(=>\angle\left(ABz\right)=\angle\left(ABC\right)+\angle\left(CBz\right)=50^o+72^o=122^o\)
\(=>\angle\left(BAx\right)+\angle\left(ABz\right)=180^o\)
mà 2 góc này ở vị trí trong cùng phía
\(=>Ax//Bz=>Ax//Cy\)

kẻ Bz//Ax=>Bz//Cy
\(=>\angle\left(BAx\right)+\angle\left(ABz\right)=180^o\)(tgosc trong cùng phía)
\(=>\angle\left(ABz\right)=180^o-100^o=80^o\)
\(=>\angle\left(CBz\right)=80+40=120^o=\angle\left(BCy\right)\)(so le trong)


Áp dụng t/c dãy tỉ số bằng nhau
\(\dfrac{a}{2013}=\dfrac{b}{2012}=\dfrac{c}{2011}=\dfrac{a-c}{2}=\dfrac{a-b}{1}=\dfrac{b-c}{1}\\ \Rightarrow a-c=2\left(a-b\right)=2\left(b-c\right)\)
\(\Rightarrow H=\dfrac{\left[2\left(a-b\right)\right]^4}{\left(a-b\right)^2\left(a-b\right)^2}=\dfrac{16\left(a-b\right)^4}{\left(a-b\right)^4}=16\)


Trả lời:
\(x=\frac{9^{11}+2}{9^{11}+3}=\frac{9^{11}+3-1}{9^{11}+3}=\frac{9^{11}+3}{9^{11}+3}-\frac{1}{9^{11}+3}=1-\frac{1}{9^{11}+3}\)
\(y=\frac{9^{12}+2}{9^{12}+3}=\frac{9^{12}+3-1}{9^{12}+3}=\frac{9^{12}+3}{9^{12}+3}-\frac{1}{9^{12}+3}=1-\frac{1}{9^{12}+3}\)
Ta có: \(9^{11}< 9^{12}\)
\(\Leftrightarrow9^{11}+3< 9^{12}+3\)
\(\Leftrightarrow\frac{1}{9^{11}+3}>\frac{1}{9^{12}+3}\)
\(\Leftrightarrow-\frac{1}{9^{11}+3}< -\frac{1}{9^{12}+3}\)
\(\Leftrightarrow1-\frac{1}{9^{11}+3}< 1-\frac{1}{9^{12}+3}\)
\(\Leftrightarrow x< y\)
Vậy x < y

\(D=\left|x-2\right|+\left|3y+9\right|+13\ge13\)
Dấu ''='' xảy ra khi x = 2 ; y = -3
Vậy GTNN của D bằng 13 tại x = 2 ; y = -3
D = 13
x = 2
y = 3
nha mình phải nghĩ lâu lắm đó
xong ko biết ra hỏi anh họ :(((
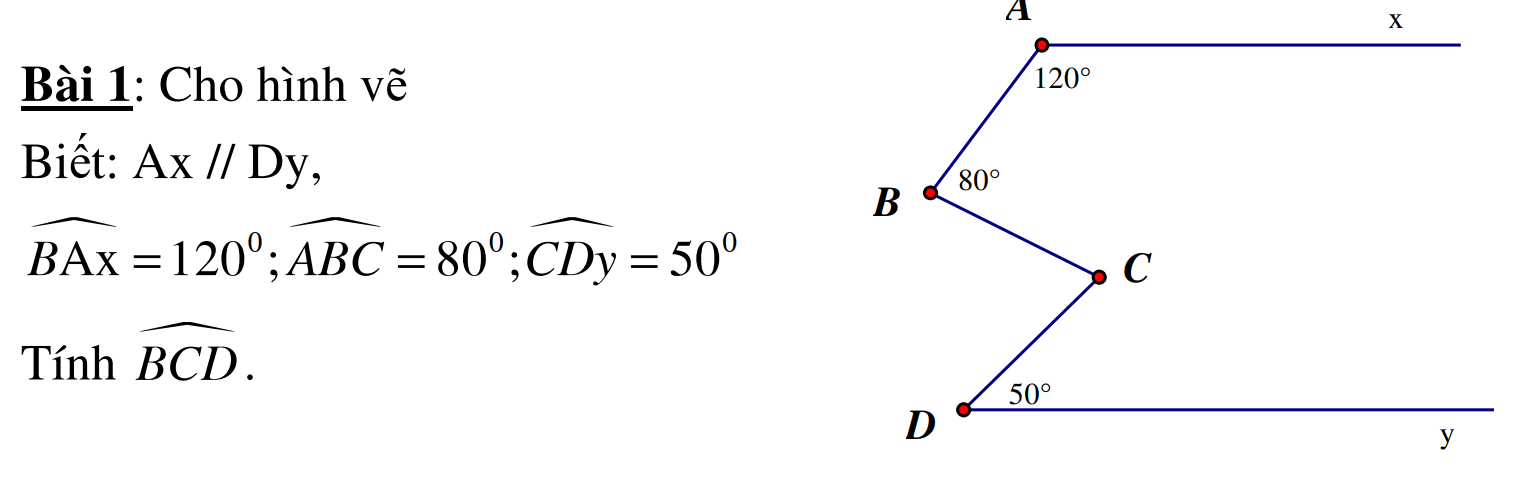
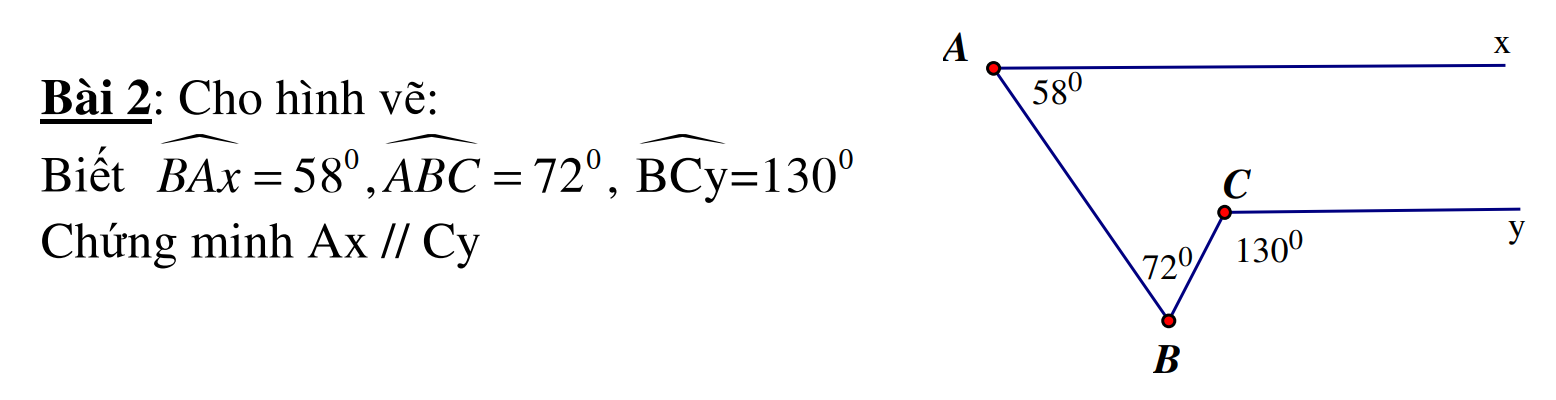
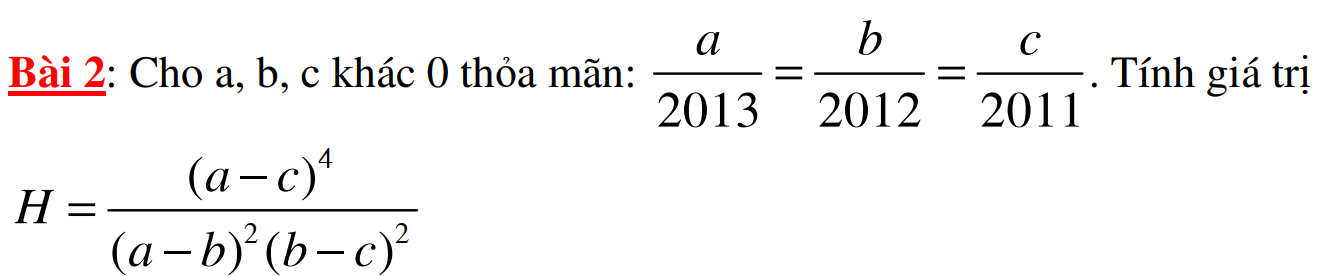
\(\frac{9}{2.5}+\frac{39}{5.8}+\frac{87}{8.11}+...+\frac{9897}{98.101}\)
\(=1-\frac{1}{2.5}+1-\frac{1}{5.8}+1-\frac{1}{8.11}+...+1-\frac{1}{98.101}\)
\(=1+1+...+1-\left(\frac{1}{2.5}+\frac{1}{5.8}+\frac{1}{8.11}+...+\frac{1}{98.101}\right)\) \(\left(\text{33 chữ số 1}\right)\)
\(=33-\frac{1}{3}\left(\frac{3}{2.5}+\frac{3}{5.8}+\frac{3}{8.11}+...+\frac{3}{98.101}\right)\)
\(=33-\frac{1}{3}\left(\frac{1}{2}-\frac{1}{5}+\frac{1}{5}-\frac{1}{8}+\frac{1}{8}-\frac{1}{11}+...+\frac{1}{98}-\frac{1}{101}\right)\)
\(=3-\frac{1}{3}\left(\frac{1}{2}-\frac{1}{101}\right)\)
\(=3-\frac{1}{3}-\frac{99}{202}\)
\(=\frac{1319}{606}\)