Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn nói trục căn thức ở mẫu là sao, mik ko hiểu. Xin lỗi vì mik ko thể giải thích cho bạn được nha.

ta có abc^2 có tận cùng là abc nên c chỉ có thể =1;5;6
nếu c=1thi ab1^2-ab1=1000n (n là 1 số tự nhiên)
suy ra ab1(ab1-1)=1000n suy ra ab1.ab0=1000n suy ra ab1.ab=100n suy ra b=0
tức là a01.a0=100n suy ra a01.a=10n suy ra a=0 dieu vo li
tương tự với a=6 và a=5 thì ta chỉ có 1 kết quả là 625



Để chứng minh rằng x là một số nguyên, chúng ta cần xác định giá trị của x và kiểm tra xem nó có phải là một số nguyên hay không. Đầu tiên, chúng ta sẽ tính giá trị của x.
Giá trị của x được tính bằng cách thực hiện các phép tính trên dấu căn bậc ba. Ta có:
x = ∛(3+√(9+125/27)) - ∛(-3+√(9+125/27))
Để tính toán giá trị này, ta cần tính giá trị căn bậc hai trong ngoặc đơn trước tiên. Hãy thực hiện phép tính này:
√(9+125/27) = √(9+4.6296) = √13.6296 ≈ 3.6923
Sau đó, ta tính giá trị căn bậc ba của biểu thức trong ngoặc đơn:
∛(3+√13.6296) ≈ ∛(3+3.6923) ≈ ∛6.6923 ≈ 1.9509
Tương tự, ta tính giá trị căn bậc ba của biểu thức còn lại:
∛(-3+√13.6296) ≈ ∛(-3+3.6923) ≈ ∛0.6923 ≈ 0.8879
Bây giờ, chúng ta có giá trị của x:
x ≈ 1.9509 - 0.8879 ≈ 1.063
Để chứng minh rằng x là một số nguyên, chúng ta cần kiểm tra xem x có là một số nguyên hay không. Trong trường hợp này, x không phải là một số nguyên vì nó có phần thập phân.
Vì vậy, ta không thể chứng minh rằng x là một số nguyên.

Câu 6: Để hàm số y=(1-m)x+3 nghịch biến trên R thì 1-m<0
=>m>1
=>Chọn B
Câu 7: D
Câu 10: (D)//(D')
=>\(\left\{{}\begin{matrix}3m+1=2\left(m+1\right)\\-2\ne-2\left(loại\right)\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
=>Chọn D
Câu 11: \(x^2+2x+2=\left(x+1\right)^2+1>=1>0\forall x\)
=>\(\sqrt{x^2+2x+2}\) luôn xác định với mọi số thực x
=>Chọn A
Câu 12: Để hai đường thẳng y=x+3m+2 và y=3x+2m+3 cắt nhau tại một điểm trên trục tung thì \(\left\{{}\begin{matrix}1\ne3\left(đúng\right)\\3m+2=2m+3\end{matrix}\right.\)
=>3m+2=2m+3
=>m=1
=>Chọn C
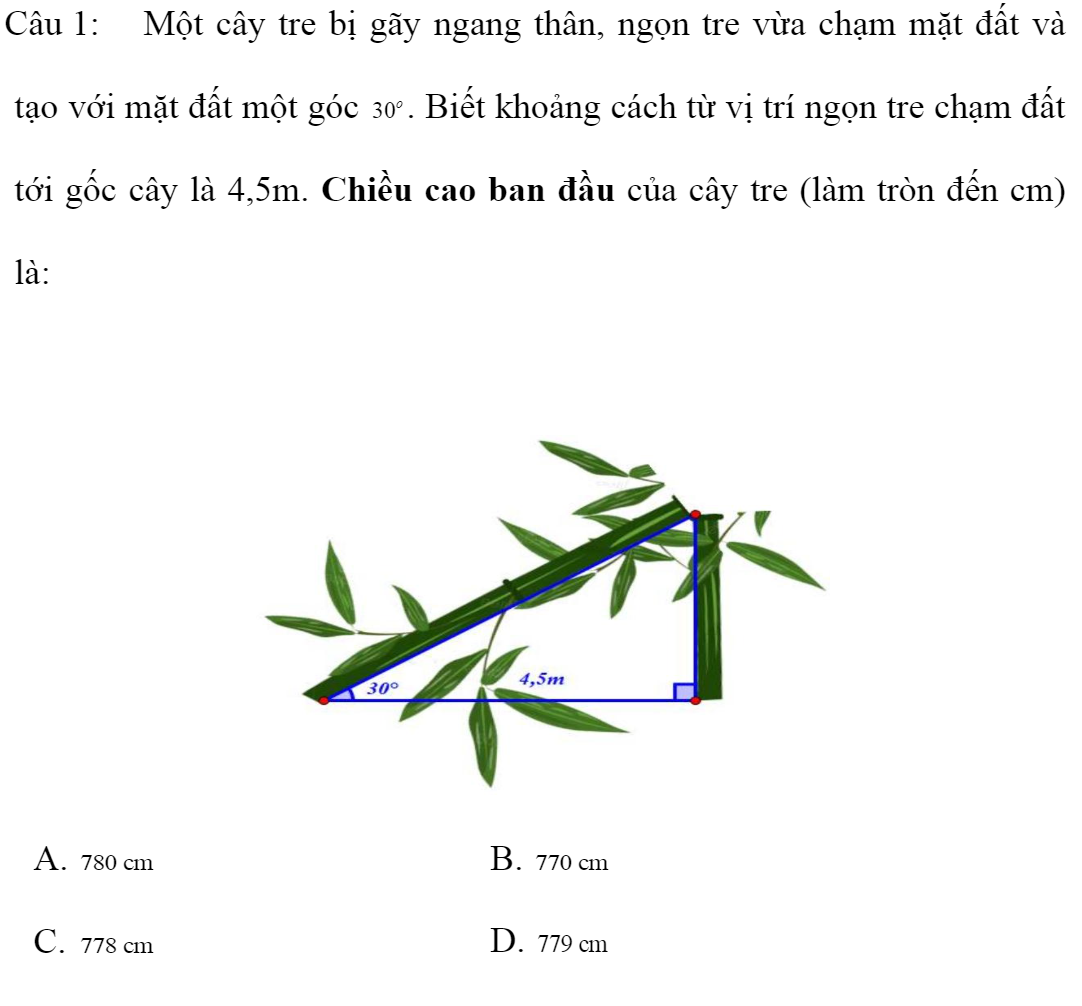

 Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)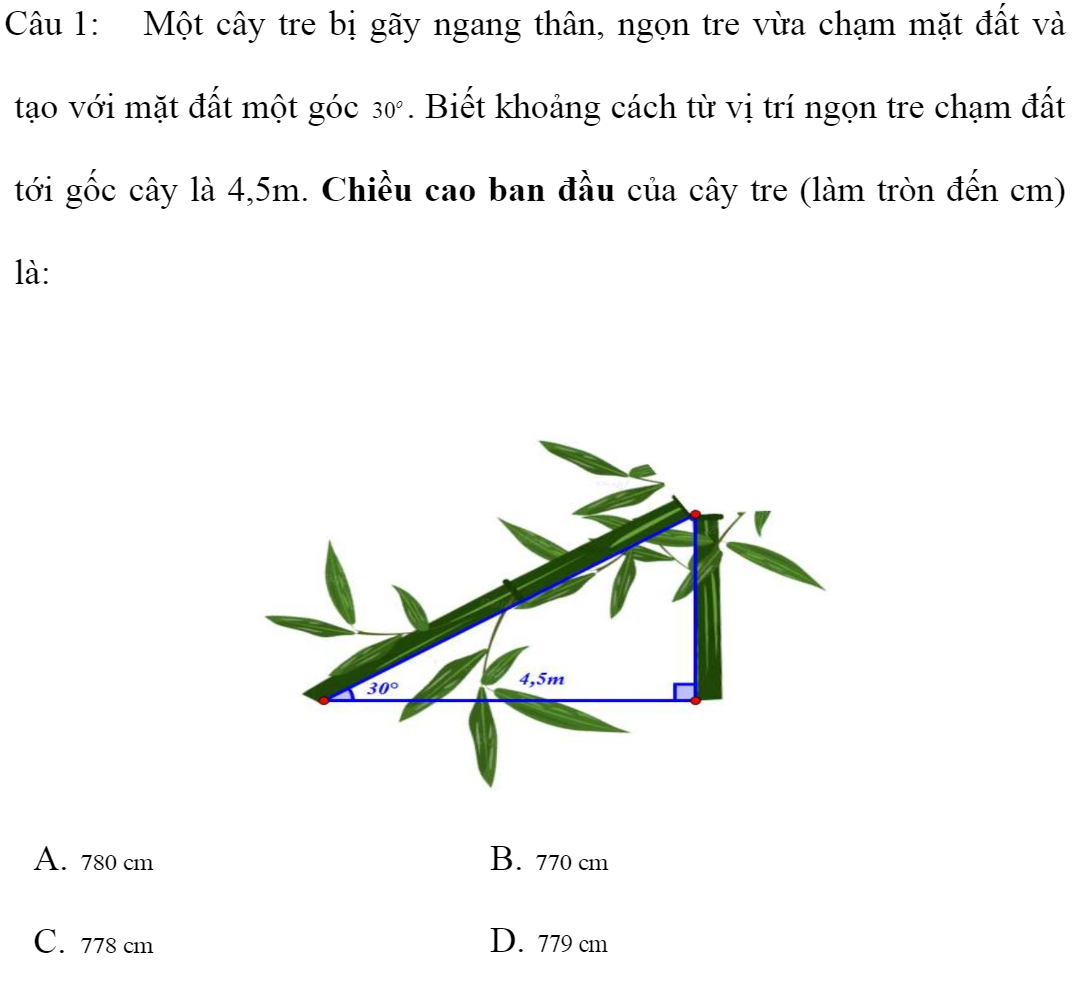



ta có : 79^9= 781=74*(20+1)= (....1)
=> 79^9 có số tận cùng là 1
9 đồng dư với 1 mod 4 => \(9^9\) đồng dư với 1 mod 4 => \(7^{9^9}\)= \(7^{4k+1}\) (k thuộc N) thì có chữ số tận cùng là 7