K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
12 tháng 4 2017
Đáp án A
P = 7 20 + 11 15 - 15 12 : 11 20 - 26 45 P = 21 60 + 44 60 - 75 60 : 99 180 - 104 180 P = - 10 60 : - 5 180 = - 10 60 . 180 - 5 = 6
Q = 5 - 5 8 + 5 9 - 5 27 8 - 8 3 + 8 9 - 8 27 : 15 - 15 11 + 1 121 16 - 16 11 + 16 121 Q = 5 1 - 1 3 + 1 9 - 1 27 8 1 - 1 3 + 1 9 - 1 27 : 15 1 - 1 11 + 1 121 16 1 - 1 11 + 1 121 Q = 5 8 : 15 16 = 5 8 . 16 15 = 2 3
Vì 6 > 2 3 nên P > Q
CM
15 tháng 2 2018
Đáp án A
P = 7 20 + 11 15 - 15 12 : 11 20 - 2 45 P = 21 60 + 44 60 - 75 60 : 99 180 - 104 180 P = - 10 60 : - 5 180 = - 10 60 . 180 - 5 = 6
Q = 5 - 5 8 + 5 9 - 5 27 8 - 8 3 + 8 9 - 8 27 : 15 - 15 11 + 15 121 16 - 16 11 + 16 121 Q = 5 1 - 1 3 + 1 9 - 1 27 8 . 1 - 1 3 + 1 9 - 1 27 : 15 1 - 1 11 + 1 121 16 . 1 - 1 11 + 1 121 Q = 5 8 : 15 16 = 5 8 . 16 15 = 2 3
Vì 6 > 2 3 nên P > Q
CM
6 tháng 6 2019
Đáp án A
P = 7 20 + 11 15 - 15 12 : 11 20 - 26 45 P = 21 60 + 44 60 - 75 60 : 99 180 - 104 180 P = - 10 60 : - 5 180 = - 10 60 . 180 - 5 = 6
Q = 5 - 5 8 + 5 9 - 5 27 8 - 8 3 + 8 9 - 8 27 : 15 - 15 11 + 1 121 16 - 16 11 + 16 121 Q = 5 1 - 1 3 + 1 9 - 1 27 8 1 - 1 3 + 1 9 - 1 27 : 15 1 - 1 11 + 1 121 16 1 - 1 11 + 1 121 Q = 5 8 : 15 16 = 5 8 . 16 15 = 2 3
Vì 6 > 2 3 nên P > Q
PK
1
8 tháng 12 2020
a là hợp số; b là hợp số ; c là hợp số; k cho tui nha
11 tháng 3 2021
Số chính phương khi chia 3 chỉ dư 0 hoặc 1.
Trường hợp 1:
\(a^2\equiv1\left(mod3\right);b^2\equiv0\left(mod3\right)\Leftrightarrow a^2+b^2\equiv1\left(mod3\right)\)(loại)
Trường hợp 2:
\(a^2\equiv1\left(mod\right)3;b^2\equiv1\left(mod3\right)\Leftrightarrow a^2+b^2\equiv2\left(mod3\right)\)(loại)
Trường hợp 3:
\(a^2\equiv0\left(mod3\right);b^2\equiv0\left(mod3\right)\Leftrightarrow a^2+b^2\equiv0\left(mod3\right)\) ( thỏa mãn )
Vậy có đpcm.
11 tháng 3 2021
Giải:
Giả sử a không ⋮ 3 ➩ b không ⋮ 3
➩\(a^2 - 1 + b^2-1\) ⋮ 3
Mà \(a^2 +b^2\)➩2⋮ 3 (không có thể)
Vậy ➩a và b ⋮ 3.
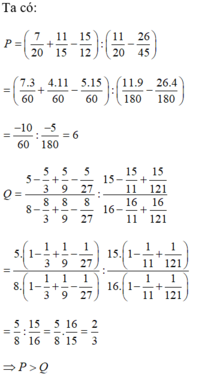
5\(^2\)
= 52 = 25