Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Vẽ hình và giải chi tiết giúp mình với, đang cần gấp cảm ơn nhiều ạ
a: Xét tứ giác AECF có
AE//CF(AB//CD)
AE=CF
Do đó: AECF là hình bình hành
b: AE+EB=AB
CF+FD=CD
mà AE=CF và AB=CD
nên BE=DF
Xét tứ giác BEDF có
BE//DF
BE=DF
Do đó: BEDF là hình bình hành
=>DE=BF
c:
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔAIC có
D,O lần lượt là trung điểm của AI,AC
=>DO là đường trung bình
=>DO//CI
d: AECF là hình bình hành
=>AC cắt EF tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của EF
=>AC,EF,BD đồng quy(do cùng đi qua O)
Mn giải giúp mik vs ạ 🥺 mình đang cần gấp. Cảm ơn mn nhiều
\(a,A=0,2\left(5x-1\right)-\dfrac{1}{2}\left(\dfrac{2}{3}x+4\right)+\dfrac{2}{3}\left(3-x\right)\)
\(=x-0,2-\dfrac{1}{3}x-2+2-\dfrac{2}{3}x\)
\(=\left(-0,2-2+2\right)+\left(x-\dfrac{1}{3}x-\dfrac{2}{3}x\right)\)
\(=-0,2\)
\(b,B=\left(x-2y\right)\left(x^2+2xy+4y^2\right)-\left(x^3-8y^3+10\right)\)
\(=x^3-8y^3-x^3+8y^3-10\)
\(=-10\)
\(c,C=4\left(x+1\right)^2+\left(2x-1\right)^2-8\left(x-1\right)\left(x+1\right)-4x\)
\(=4\left(x^2+2x+1\right)+\left(4x^2-4x+1\right)-8\left(x^2-1\right)-4x\)
\(=4x^2+8x+4+4x^2-4x+1-8x^2+8-4x\)
\(=13\)
a) \(A=0,2\left(5x-1\right)-\dfrac{1}{2}\left(\dfrac{2}{3}x+4\right)+\dfrac{2}{3}\left(3-x\right)\)
\(A=x-\dfrac{1}{5}-\dfrac{1}{3}x-2+2-\dfrac{2}{3}x\)
\(A=\left(x-\dfrac{1}{3}x-\dfrac{2}{3}x\right)-\left(\dfrac{1}{5}+2-2\right)\)
\(A=-\dfrac{1}{5}\)
Vậy: ...
b) \(B=\left(x-2y\right)\left(x^2+2xy+4y^2\right)-\left(x^3-8y^3+10\right)\)
\(B=\left[x^3-\left(2y\right)^3\right]-\left[x^3-\left(2y\right)^3\right]-10\)
\(B=-10\)
Vậy: ...
c) \(4\left(x+1\right)^2+\left(2x-1\right)^2-8\left(x+1\right)\left(x-1\right)-4x\)
\(=4\left(x^2+2x+4\right)+\left(4x^2-4x+1\right)-8\left(x^2-1\right)-4x\)
\(=4x^2+8x+4+4x^2-4x+1-8x^2+8-4x\)
\(=\left(4x^2+4x^2-8x^2\right)+\left(8x-4x-4x\right)+\left(4+1+8\right)\)
\(=13\)
Vậy:...
(3x-4-x-1)(3x-4+x+1)=0
(2x-5)(4x-3)=0
2x-5 = 0 hoặc 4x-3=0
2x=5 hoặc 4x=3
x=5/2 hoặc x=3/4
\(M=\left|x-1\right|+\left|x-3\right|=\left|x-1\right|+\left|3-x\right|\)
Áp dụng bđt \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\) ta có:
\(M\ge\left|x-1+3-x\right|=\left|2\right|=2\)
Dấu " = " xảy ra khi \(x-1\ge0;3-x\ge0\)
\(\Rightarrow x\ge1;x\le3\)
\(\Rightarrow1\le x\le3\)
Vậy \(MIN_M=2\) khi \(1\le x\le3\)
Gọi E là giao điểm của AC và BD.
∆ECD có ∠C1 = ∠D1 (do ∠ACD = ∠BDC) nên là tam giác cân.
Suy ra EC = ED (1)
Tương tự ∆EAB cân tại A suy ra: EA = EB (2)
Từ (1) và (2) ta có: EA + EC = EB + ED ⇒ AC = BD
Hình thang ABCD có hai đường chéo bằng nhau nên là hình thang cân.4
a) \(Q=\dfrac{\left(x+2\right)^2}{x}\cdot\left(1-\dfrac{x^2}{x+2}\right)-\dfrac{x^2+10x+4}{x}\left(x\ne0;x\ne-2\right)\)
\(Q=\dfrac{\left(x+2\right)^2}{x}\cdot\dfrac{\left(x+2\right)-x^2}{x+2}-\dfrac{x^2+10x+4}{x}\)
\(Q=\dfrac{\left(x+2\right)^2}{x}\cdot\dfrac{-x^2+x+2}{x+2}-\dfrac{x^2+10x+4}{x}\)
\(Q=\dfrac{\left(x+2\right)\left(-x^2+x+2\right)}{x}-\dfrac{x^2+10x+4}{x}\)
\(Q=\dfrac{-x^3+x^2+2x-2x^2+2x+4-x^2-10x-4}{x}\)
\(Q=\dfrac{-x^3-2x^2-6x}{x}\)
\(Q=\dfrac{x\left(-x^2-2x-6\right)}{x}\)
\(Q=-x^2-2x-6\)
b) Ta có:
\(Q=-x^2-2x-6\)
\(Q=-\left(x^2+2x+6\right)\)
\(Q=-\left[\left(x^2+2x+1\right)+5\right]\)
\(Q=-\left(x+1\right)^2-5\)
Mà: \(-\left(x+1\right)^2\le0\forall x\)
\(\Rightarrow Q=-\left(x+1\right)^2-5\le-5\forall x\)
Dấu "=" xảy ra khi:
\(x+1=0\Rightarrow x=-1\)
Vậy: \(Q_{max}=-5\Leftrightarrow x=-1\)
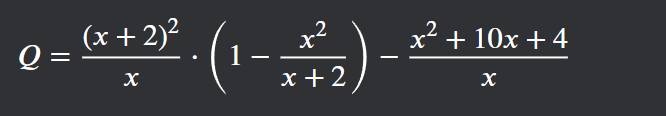
3.(⅓x - ¼)² = ⅓
=> (\(\dfrac{1}{3x}\)- \(\dfrac{1}{4}\) )2 = \(\dfrac{1}{9}\)
=>\(\left[{}\begin{matrix}\dfrac{1}{3x}-\dfrac{1}{4}=\dfrac{-1}{3}\\\dfrac{1}{3x}-\dfrac{1}{4}=\dfrac{1}{3}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\dfrac{1}{3x}=\dfrac{-1}{12}\\\dfrac{1}{3x}=\dfrac{7}{12}\end{matrix}\right.\) => \(\left[{}\begin{matrix}x=-4\\x=\dfrac{12}{21}=\dfrac{4}{7}\end{matrix}\right.\)
Vậy, tập nghiệm x thỏa mãn là S=\(\left\{-4;\dfrac{4}{7}\right\}\)