
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


-Ta có: \(2x.x=0\)
\(\Rightarrow2x^2=0\)
\(\Rightarrow x^2=0\)
\(\Rightarrow x=0\)
-Vậy nghiệm của đa thức là \(x=0\)

2D
6
\(x^3+125=\left(x+5\right)\left(x^2-5x+25\right)\)
A là đa thức bậc 1
=>A=x+5
=>B=x^2-5x+25
=>Chọn A
Câu 2. M có bậc 2 + 7 = 9
Chọn D
Câu 6. x³ + 125 = x³ + 5³ = (x + 5)(x² - 5x + 25)
Chọn A

Lời giải:
a) $(a+b-c)x^2-(c-a-b)x=(a+b-c)x^2+(a+b-c)x$
$=(a+b-c)x(x+1)$
b) $2x.x-1-1-x=2x^2-x-2$: biểu thức này không phân tích được thành nhân tử.
c) $9x.x-y-10y-x^2=9x^2-11y-x^2=8x^2-11y$ không phân tích được thành nhân tử
d) $x-1^2-2-x^3=x-3-x^3$ không phân tích được thành nhân tử.


a: \(x^4+4=\left(x^2-2x+2\right)\left(x^2+2x+2\right)\)
b: \(x^8+x^7+1\)
\(=x^8+x^7+x^6-x^6-x^5-x^4+x^5+x^4+x^3-x^3-x^2-x+x^2+x+1\)
\(=\left(x^2+x+1\right)\left(x^6-x^4+x^3-x+1\right)\)
c: \(x^8+x^4+1\)
\(=\left(x^8+2x^4+1\right)-x^4\)
\(=\left(x^4-x^2+1\right)\cdot\left(x^4+x^2+1\right)\)
\(=\left(x^4-x^2+1\right)\left(x^2+1-x\right)\left(x^2+1+x\right)\)

11) Ta có: \(a^6+a^4+a^2b^2+b^4-b^6\)
\(=a^6-b^6+a^4+a^2b^2+b^4\)
\(=\left(a^2-b^2\right)\left(a^4+a^2b^2+b^4\right)+\left(a^4+a^2b^2+b^4\right)\)
\(=\left(a^4+a^2b^2+b^4\right)\left(a^2-b^2+1\right)\)
12) Ta có: \(x^3+3xy+y^3-1\)
\(=\left(x^3+3x^2y+3xy^2+y^3-1\right)-3x^2y-3xy^2+3xy\)
\(=\left[\left(x+y\right)^3-1\right]-3xy\left(x+y-1\right)\)
\(=\left(x+y-1\right)\left[x^2+2xy+y^2+x+y+1\right]-3xy\left(x+y-1\right)\)
\(=\left(x+y-1\right)\left(x^2-xy+y^2+x+y+1\right)\)
14) Ta có: \(x^8+x+1\)
\(=x^8+x^7-x^7-x^6+x^6+x^5-x^5-x^4+x^4+x^3-x^3+x^2-x^2+x+1\)
\(=x^6\left(x^2+x+1\right)-x^5\left(x^2+x+1\right)+x^3\left(x^2+x+1\right)-x^2\left(x^2+x+1\right)+\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left(x^6-x^5+x^3-x^2+1\right)\)
15) Ta có: \(x^8+3x^4+4\)
\(=x^8+4x^4+4-x^4\)
\(=\left(x^4+2\right)^2-\left(x^2\right)^2\)
\(=\left(x^4-x^2+2\right)\left(x^4+x^2+2\right)\)
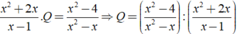
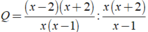
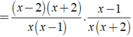
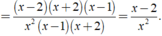
Không có giá trị x nào thỏa mãn