K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 8 2023
\(A=\left(2x^2+2y^2+5\right)\left(x^2+y^2\right)\)
=2x^2+2y^2+5
=2(x^2+y^2)+5
=2+5
=7
SS
17 tháng 8 2019
A= 2x^2 + y^2 - 2xy -2x+3
A= x^2-2xy + y^2 + x^2 - 2x+ 1 +2
A= (x-y)^2 + (x-1)^2 + 2
(x-y)^2> hoặc = 0 với mọi giá trị của x
(x-1)^2 > hoặc =0 với mọi giá trị của x
=> (x-y)^2 + (x-1)^2 > hoặc =0 với mọi giá trị của x
=> (x-y)^2 + (x-1)^2 + 2 > hoặc =2
=> A lớn hơn hoặc bằng 2
=> GTNN của A=2 tại x=y=1
26 tháng 9 2021
\(C=\left(x^2-2xy+y^2\right)\left(x^2+y^2\right)-2x^3y-3x^3y^2+2xy^3\)
\(=\left(x^2+y^2\right)^2-2xy\left(x^2+y^2\right)-xy\left(2x^2+3x^2y+2y^2\right)\)
\(=\left(x^2+y^2\right)^2-xy\left(2x^2+2y^2+2x^2+3x^2y+2y^2\right)\)
\(=\left(x^2+y^2\right)^2-xy\left(4x^2+3x^2y+4y^2\right)\)
MS
1
LN
10 tháng 10 2021
\(a,x^2-2xy+y^2-z^2=\left(x-y\right)^2-z^2=\left(x-y-z\right).\left(x-y+z\right)\)
\(b,x^3+y^3+2x^2-2xy+2y^2=\left(x^3+y^3\right)+2\left(x^2-xy+y^2\right)=\left(x+y\right).\left(x^2-2xy+y^2\right)+2.\left(x^2-xy+y^2\right)=\left(x^2-xy+y^2\right).\left(x+y+2\right)\)
KR
7 tháng 5 2018
Áp dụng Bunyakovsky, ta có :
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x.1+y.1\right)^2=1\)
=> \(\left(x^2+y^2\right)\ge\frac{1}{2}\)
=> \(Min_C=\frac{1}{2}\Leftrightarrow x=y=\frac{1}{2}\)
Mấy cái kia tương tự
CM
3 tháng 11 2018
Ta có
M = 3 x 2 ( x 2 + y 2 ) + 3 y 2 ( x 2 + y 2 ) – 5 ( y 2 + x 2 ) = ( x 2 + y 2 ) ( 3 x 2 + 3 y 2 – 5 ) = ( x 2 + y 2 ) [ 3 ( x 2 + y 2 ) – 5 ]
Mà x 2 + y 2 = 1 nên M = 1.(3.1 – 5) = -2. Vậy M = -2
Đáp án cần chọn là: D
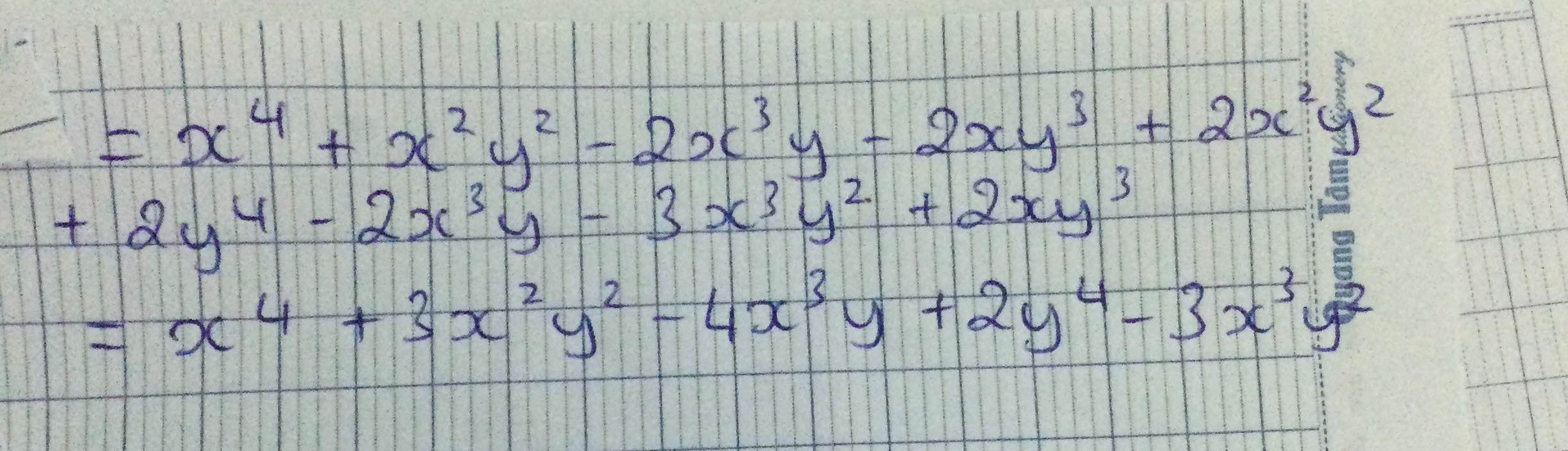
\(2x^2\left(x^2+y^2\right)+2y^2\left(x^2+y^2\right)+5\left(y^2+x^2\right)\)
\(=\left(x^2+y^2\right)\left(2x^2+2y^2\right)+5\left(x^2+y^2\right)\)
\(=2\left(x^2+y^2\right)\left(x^2+y^2\right)+5\left(x^2+y^2\right)\)
\(=2\left(x^2+y^2\right)^2+5\left(x^2+y^2\right)\)
Thay \(x^2+y^2=1\) vào ta có:
\(2\cdot1^2+5\cdot1=2+5=7\)