Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,3\left(2x-3\right)+2\left(2-x\right)=-3\\ \Leftrightarrow6x-9+4-2x=-3\\ \Leftrightarrow4x=2\\ \Leftrightarrow x=\dfrac{1}{2}\\ b,x\left(5-2x\right)+2x\left(x-1\right)=13\\ \Leftrightarrow5x-2x^2+2x^2-2x=13\\ \Leftrightarrow3x=13\\ \Leftrightarrow x=\dfrac{13}{3}\\ c,5x\left(x-1\right)-\left(x+2\right)\left(5x-7\right)=6\\ \Leftrightarrow5x^2-5x-5x^2-3x+14=6\\ \Leftrightarrow-8x=-8\\ \Leftrightarrow x=1\\ d,3x\left(2x+3\right)-\left(2x+5\right)\left(3x-2\right)=8\\ \Leftrightarrow6x^2+9x-6x^2-11x+10=8\\ \Leftrightarrow-2x=-2\\ \Leftrightarrow x=1\)
\(e,2\left(5x-8\right)-3\left(4x-5\right)=4\left(3x-4\right)+11\\ \Leftrightarrow10x-16-12x+15=12x-16+11\\ \Leftrightarrow-14x=-4\\ \Leftrightarrow x=\dfrac{2}{7}\\ f,2x\left(6x-2x^2\right)+3x^2\left(x-4\right)=8\\ \Leftrightarrow12x^2-4x^3+3x^3-12x^2=8\\ \Leftrightarrow-x^3-8=0\\ \Leftrightarrow-\left(x^3+8\right)=0\\ \Leftrightarrow-\left(x+2\right)\left(x^2-2x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-2\\x\in\varnothing\left(x^2-2x+4=\left(x-1\right)^2+3>0\right)\end{matrix}\right.\)
Bài 4:
a: Ta có: \(3\left(2x-3\right)-2\left(x-2\right)=-3\)
\(\Leftrightarrow6x-9-2x+4=-3\)
\(\Leftrightarrow4x=2\)
hay \(x=\dfrac{1}{2}\)
b: Ta có: \(x\left(5-2x\right)+2x\left(x-1\right)=13\)
\(\Leftrightarrow5x-2x^2+2x^2-2x=13\)
\(\Leftrightarrow3x=13\)
hay \(x=\dfrac{13}{3}\)
c: Ta có: \(5x\left(x-1\right)-\left(x+2\right)\left(5x-7\right)=6\)
\(\Leftrightarrow5x^2-5x-5x^2+7x-10x+14=6\)
\(\Leftrightarrow-8x=-8\)
hay x=1

+) (5x-1). (2x+3)-3. (3x-1)=0
10x^2+15x-2x-3 - 9x+3=0
10x^2 +8x=0
2x(5x+4)=0
=> x=0 hoặc x= -4/5
+) x^3 (2x-3)-x^2 (4x^2-6x+2)=0
2x^4 -3x^3 -4x^4 + 6x^3 - 2x^2=0
-2x^4 + 3x^3-2x^2=0
x^2(-2x^2+x-2)=0
-2x^2(x-1)^2=0
=> x=0 hoặc x=1
+) x (x-1)-x^2+2x=5
x^2 -x -x^2+2x=5
x=5
+) 8 (x-2)-2 (3x-4)=25
8x - 16-6x+8=25
2x=33
x=33/2

2: =(2x+1)^2-y^2
=(2x+1+y)(2x+1-y)
3: =x^2(x^2+2x+1)
=x^2(x+1)^2
4: =x^2+6x-x-6
=(x+6)(x-1)
5: =-6x^2+3x+4x-2
=-3x(2x-1)+2(2x-1)
=(2x-1)(-3x+2)
6: =5x(x+y)-(x+y)
=(x+y)(5x-1)
7: =2x^2+5x-2x-5
=(2x+5)(x-1)
8: =(x^2-1)*(x^2-4)
=(x-1)(x+1)(x-2)(x+2)
9: =x^2(x-5)-9(x-5)
=(x-5)(x-3)(x+3)

1: Ta có: \(\left(x+3\right)^2-\left(x+2\right)\left(x-2\right)=4x+17\)
\(\Leftrightarrow x^2+6x+9-x^2+4-4x=17\)
\(\Leftrightarrow x=2\)
3: Ta có: \(\left(2x+3\right)\left(x-1\right)+\left(2x-3\right)\left(1-x\right)=0\)
\(\Leftrightarrow2x^2-2x+3x-3+2x-2x^2-3+3x=0\)
\(\Leftrightarrow6x=6\)
hay x=1

v) \(\left(-\dfrac{1}{2}x+3\right)\left(2x+6-4c^3\right)\)
\(=-\dfrac{1}{2}\left(2x+6-4c^3\right)+3\left(2x+6-4c^3\right)\)
\(=-x^2-3x+2c^3x+6x+18-12c^3\)
\(=-x^2+3x+2c^3x+18-12c^3\)
f) \(\left(2x-5\right)\left(x^2-x+3\right)\)
\(=2x\left(x^2-x+3\right)-5\left(x^2-x+3\right)\)
\(=2x^3-2x^2+6x-5x^2+5x-15\)
\(=2x^3-7x^2+11x-15\)
w) \(\left(3x+1\right)\left(x^2-2x-5\right)\)
\(=3x\left(x^2-2x-5\right)+\left(x^2-2x-5\right)\)
\(=3x^3-6x^2-15x+x^2-2x-5\)
\(=3x^3-5x^2-17x-5\)
x) \(\left(6x-3\right)\left(x^2+x-1\right)\)
\(=6x\left(x^2+x-1\right)-3\left(x^2+x-1\right)\)
\(=6x^3+6x^2-6x-3x^2-3x+3\)
\(=6x^3+3x^2-9x+3\)
y) \(\left(5x-2\right)\left(3x+1-x^2\right)\)
\(=5x\left(3x+1-x^2\right)-2\left(3x+1-x^2\right)\)
\(=15x^2+5x-5x^3-6x-2+2x^2\)
\(=-5x^3+17x^2-x-2\)
z) \(\left(\dfrac{3}{4}x+1\right)\left(4x^2+4x+4\right)\)
\(=\dfrac{3}{4}x\left(4x^2+4x+4\right)+\left(4x^2+4x+4\right)\)
\(=3x^3+3x^2+3x+4x^2+4x+4\)
\(=3x^3+7x^2+7x+4\)
f: =2x^3-2x^2+6x-5x^2+5x-15
=2x^3-7x^2+11x-15
w: =3x^3-6x^2-15x+x^2-2x-5
=3x^3-5x^2-17x-5
x: =6x^3+6x^2-6x-3x^2-3x+3
=6x^3+3x^2-9x+3
y: =(5x-2)(-x^2+3x+1)
=-5x^3+15x^2+5x+2x^2-6x-2
=-5x^3+17x^2-x-2
z: =3x^3+3x^2+3x+4x^2+4x+4
=3x^3+7x^2+7x+4

\(a,2x^3+5x^2+5x+3\)
\(=2x^3+3x^2+2x^2+3x+2x+3\)
\(=x^2\left(2x+3\right)+x\left(2x+3\right)+\left(2x+3\right)\)
\(=\left(2x+3\right)\left(x^2+x+1\right)\)

a: \(=\dfrac{2\left(x+2\right)\left(x-1\right)}{x+2}=2x-2\)
b: \(=\dfrac{2x^3+x^2-6x^2-3x+2x+1}{2x+1}=x^2-3x+1\)
c: \(=\dfrac{x^3+2x^2-2x^2-4x+2x+4}{x+2}=x^2-2x+2\)
d: \(=\dfrac{x^2\left(x-3\right)}{x-3}=x^2\)

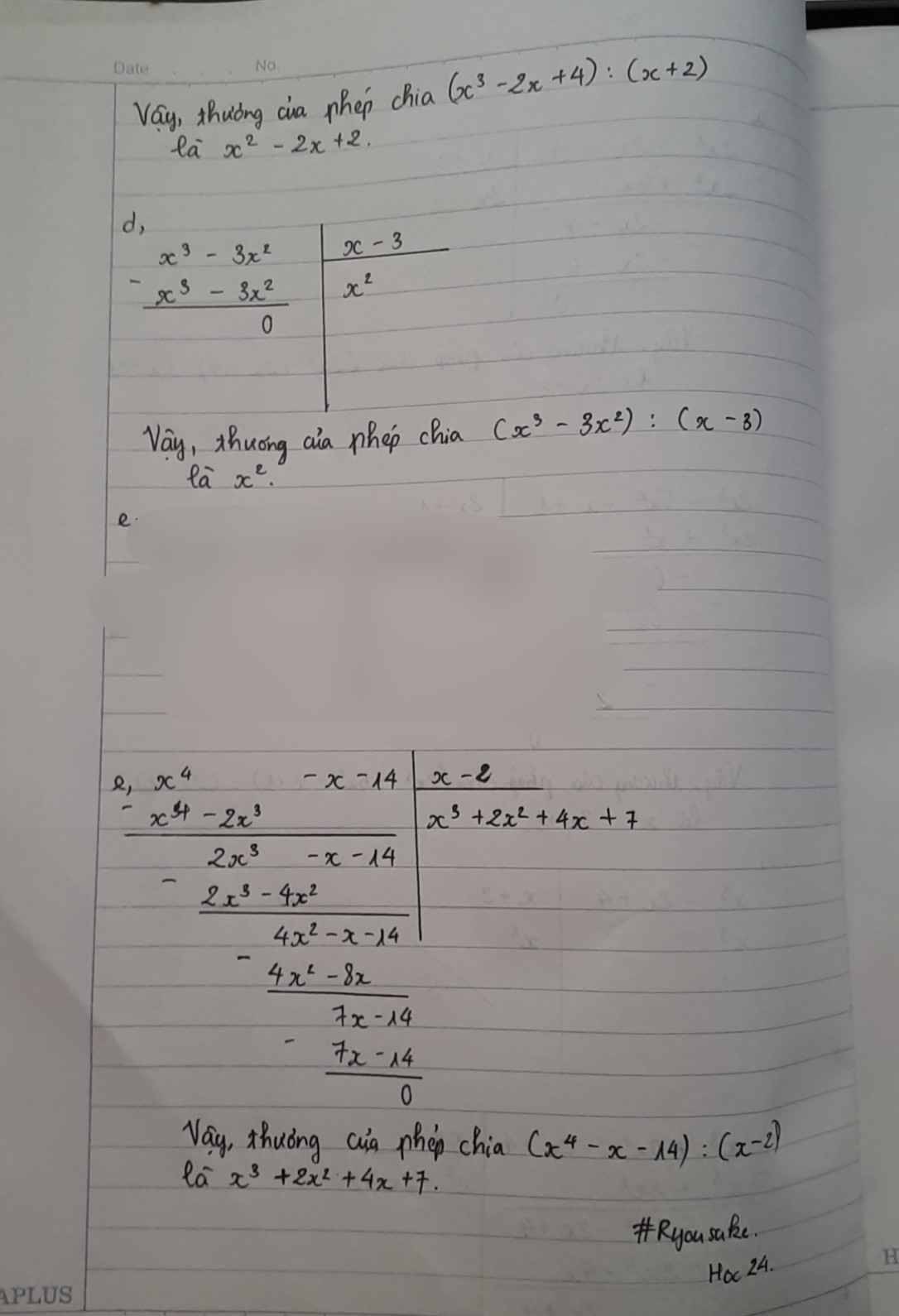

d: \(\dfrac{x^4-2x^3+2x-1}{x^2-1}\)
\(=\dfrac{\left(x^2-1\right)\left(x^2+1\right)-2x\left(x^2-1\right)}{x^2-1}\)
\(=x^2-2x+1\)
\(=\left(x-1\right)^2\)
sao làm có 1 ý vậy bạn ơi