Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi M và N lần lượt là giao điểm của AE, BF với CD.
Ta có: A D E ^ = 1 2 D ^ ngoài, D A E ^ = 1 2 A ^ ngoài.
Mà A ^ ngoài + D ^ ngoài = 1800 (do AB//CD)
⇒ A D E ^ + D A E ^ = 90 0 , tức là tam giác ADE vuông tại E.
Khi đó, tam giác ADM cân tại D (do có DE vừa là đường phân giác, vừa là đường cao) và E là trung điểm của AM.
Chứng minh tương tự, ta được F olaf trung điểm của BN.
Từ khó, suy ra EF là đường trung bình của hình thang ABNM và ta được ĐPCM
b) Từ ý a), EF = 1 2 ( A B + B C + C D + D A )
a:
góc AMD=180 độ-góc MAD-góc MDA
\(=180^0-\dfrac{180^0-\widehat{BAD}}{2}-\dfrac{180^0-\widehat{ADC}}{2}\)
\(=180^0-\dfrac{1}{2}\widehat{ADC}-90^0+\dfrac{1}{2}\widehat{ADC}=90^0\)
Gọi giao của AM với DC là M'
Xét ΔDM'A có
DM là đường cao, là đường phân giác
nên ΔDM'A cân tại D
=>M là trung điểm của AM'
Gọi giao của BN với DC là N'
Ta có: \(\widehat{BNC}=180^0-\widehat{NBC}-\widehat{NCB}\)
\(=180^0-\dfrac{180^0-\widehat{ABC}}{2}-\dfrac{180^0-\widehat{BCD}}{2}\)
\(=180^0-90^0+\dfrac{1}{2}\widehat{ABC}-90^0+\dfrac{1}{2}\widehat{BCD}\)
=90 độ
Xét ΔCN'B có
CN vừa là đường cao, vừa là phân giác
nên ΔCN'B cân tại C
=>N là trug điểm của BN'
Xét hình thang ABN'M' có
M,N lần lượt là trung điểm của AM' và BN'
nen MN là đường trung bình
=>MN//CD//AB
b: MN=(AB+M'N')/2
=(AB+M'D+CD+CN')/2
mà M'D=AD và CN'=CB
nên MN=(AB+CD+AD+CB)/2
=>CABCD=8cm

a:
góc AMD=180 độ-góc MAD-góc MDA
\(=180^0-\dfrac{180^0-\widehat{BAD}}{2}-\dfrac{180^0-\widehat{ADC}}{2}\)
\(=180^0-\dfrac{1}{2}\widehat{ADC}-90^0+\dfrac{1}{2}\widehat{ADC}=90^0\)
Gọi giao của AM với DC là M'
Xét ΔDM'A có
DM là đường cao, là đường phân giác
nên ΔDM'A cân tại D
=>M là trung điểm của AM'
Gọi giao của BN với DC là N'
Ta có: \(\widehat{BNC}=180^0-\widehat{NBC}-\widehat{NCB}\)
\(=180^0-\dfrac{180^0-\widehat{ABC}}{2}-\dfrac{180^0-\widehat{BCD}}{2}\)
\(=180^0-90^0+\dfrac{1}{2}\widehat{ABC}-90^0+\dfrac{1}{2}\widehat{BCD}\)
=90 độ
Xét ΔCN'B có
CN vừa là đường cao, vừa là phân giác
nên ΔCN'B cân tại C
=>N là trug điểm của BN'
Xét hình thang ABN'M' có
M,N lần lượt là trung điểm của AM' và BN'
nen MN là đường trung bình
=>MN//CD//AB
b: MN=(AB+M'N')/2
=(AB+M'D+CD+CN')/2
mà M'D=AD và CN'=CB
nên MN=(AB+CD+AD+CB)/2
=>CABCD=14cm

a:
góc AMD=180 độ-góc MAD-góc MDA
\(=180^0-\dfrac{180^0-\widehat{BAD}}{2}-\dfrac{180^0-\widehat{ADC}}{2}\)
\(=180^0-\dfrac{1}{2}\widehat{ADC}-90^0+\dfrac{1}{2}\widehat{ADC}=90^0\)
Gọi giao của AM với DC là M'
Xét ΔDM'A có
DM là đường cao, là đường phân giác
nên ΔDM'A cân tại D
=>M là trung điểm của AM'
Gọi giao của BN với DC là N'
Ta có: \(\widehat{BNC}=180^0-\widehat{NBC}-\widehat{NCB}\)
\(=180^0-\dfrac{180^0-\widehat{ABC}}{2}-\dfrac{180^0-\widehat{BCD}}{2}\)
\(=180^0-90^0+\dfrac{1}{2}\widehat{ABC}-90^0+\dfrac{1}{2}\widehat{BCD}\)
=90 độ
Xét ΔCN'B có
CN vừa là đường cao, vừa là phân giác
nên ΔCN'B cân tại C
=>N là trug điểm của BN'
Xét hình thang ABN'M' có
M,N lần lượt là trung điểm của AM' và BN'
nen MN là đường trung bình
=>MN//CD//AB
b: MN=(AB+M'N')/2
=(AB+M'D+CD+CN')/2
mà M'D=AD và CN'=CB
nên MN=(AB+CD+AD+CB)/2
=>CABCD=14cm

a/ AB //CD (với AB < CD) phân giác góc ngoài tại và D cắt nhau tại M, --> AM vuông góc MD (phân giác của hai góc bù nhau), AM kéo dài cắt DC tại Q Trong tg AQD có DM phân giác và đường cao -->
tg ADQ cân ại D --> M trung điểm AQ
--> tương tự BN và BN vuông góc CN và BN kéo dài cắt DC tại R --> tg BCR cân tại C và N trung điểm BR --> MN đườn trung bình của tg của hình thang ABRQ --> MN // AB --> MN // CD
b/ Trong hình hang ARBQ có 2MN = AB + QR (MN đường trung bình của hình thang ARBQ)
--> 16 = AB + QD + CD + CP = AB + AD + CD + BC ( vì QD = AD, CR = BC)
--> Chu vi hình thang = 16 cm

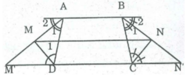
Gọi M' và N' là giao điểm của tia AM và BN với CD.
Ta có: ∠ (M') = ∠ A 2 (sole trong)
∠ A 1 = ∠ A 2 (gt)
⇒ ∠ (M') = ∠ A 1 nên ∆ ADM' cân tại D
* DM là phân giác của ∠ (ADM' )
Suy ra: DM là đường trung tuyến (tính chất tam giác cân)
⇒ AM = MM'
∠ (N') = ∠ B 1 nên ∆ BCN' cân tại C.
* CN là phân giác của ∠ (BCN')
Suy ra: CN là đường trung tuyến (tính chất tam giác cân)
⇒ BN = NN'
Suy ra: MN là đường trung bình của hình thang ABN'M'
⇒ MN // M'N' (tính chất đường trung hình hình thang)
Hay MN//CD

a:
góc AMD=180 độ-góc MAD-góc MDA
\(=180^0-\dfrac{180^0-\widehat{BAD}}{2}-\dfrac{180^0-\widehat{ADC}}{2}\)
\(=180^0-\dfrac{1}{2}\widehat{ADC}-90^0+\dfrac{1}{2}\widehat{ADC}=90^0\)
Gọi giao của AM với DC là M'
Xét ΔDM'A có
DM là đường cao, là đường phân giác
nên ΔDM'A cân tại D
=>M là trung điểm của AM'
Gọi giao của BN với DC là N'
Ta có: \(\widehat{BNC}=180^0-\widehat{NBC}-\widehat{NCB}\)
\(=180^0-\dfrac{180^0-\widehat{ABC}}{2}-\dfrac{180^0-\widehat{BCD}}{2}\)
\(=180^0-90^0+\dfrac{1}{2}\widehat{ABC}-90^0+\dfrac{1}{2}\widehat{BCD}\)
=90 độ
Xét ΔCN'B có
CN vừa là đường cao, vừa là phân giác
nên ΔCN'B cân tại C
=>N là trug điểm của BN'
Xét hình thang ABN'M' có
M,N lần lượt là trung điểm của AM' và BN'
nen MN là đường trung bình
=>MN//CD//AB
b: MN=(AB+M'N')/2
=(AB+M'D+CD+CN')/2
mà M'D=AD và CN'=CB
nên MN=(AB+CD+AD+CB)/2

Gọi trung điểm của AD là P
trung điểm của BC là Q
=>PQ là đường trung bình của hình thang ABCD
=>MN//DC
Lại có góc ngoài của góc A và D kề nhau
=> hai tia phân giác của góc này hợp với nhau 1 góc 90 độ => góc M =90 độ
Tương tự có góc N =90 độ
Xét tam giác AMD có góc M =90 độ
P là trung điểm của AD
=> MP=PA=> tam giác MPA cân ở P => Góc MAP = góc AMP => MP//AB
Tương tự có QN//AB
mà MN//AB =>M, P, Q, N thẳng hàng
=>mn//\ba. Mà BA//DC => MN//DC
Bạn cho mình hỏi, ở đoạn suy ra PQ là đường trung bình của hình thang ABCD, rồi suy ra MN //DC là sao? Nếu đã suy ra được rồi thì cần gì phải chứng minh đoạn dưới nữa. Ở phần đó, bạn có viết nhầm hay không? Bạn giải thích giúp mình với