2^3.5^3-3.{400-[673-2^3.(7^3:7+1)]}. ko cần mọi người trả lời

Khách

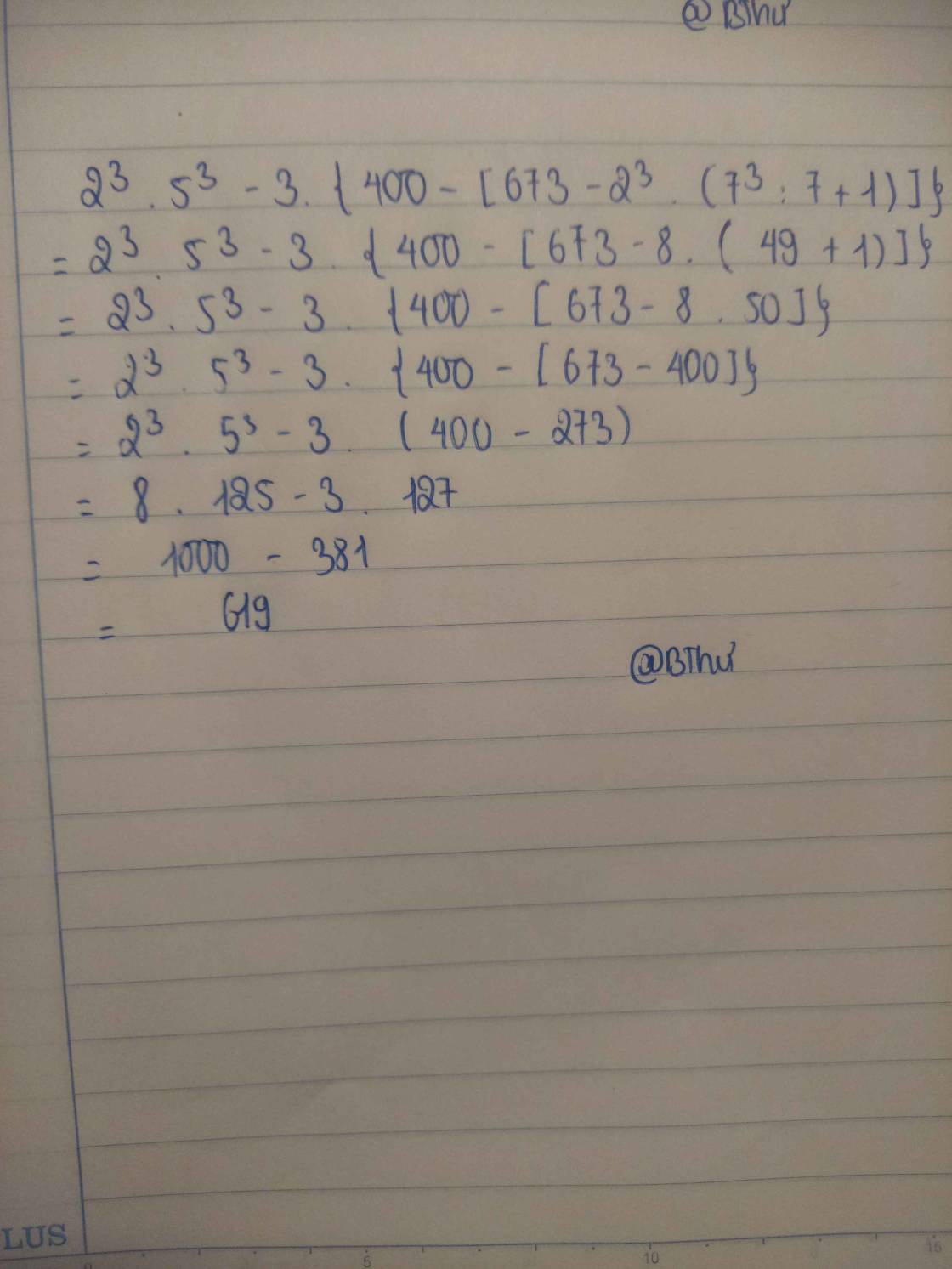
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Nguyễn Tiến Đạt

20 tháng 2 2023 - olm

2^3.5^3-3.{400-[673-2^3.(7^3:7+1)]}. ko cần mọi người trả lời

#Toán lớp 6

⭐Hannie⭐

20 tháng 2 2023

Đúng(5)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Owari and Shiona

27 tháng 3 2018 - olm

Câu 1 :Thực hiện phép tính A= \(\frac{2^5.7+2^5}{2^5.3^2-2^5}\)

Câu 2 Tính giá trị của biểu thức B = \(2^3.5^3-3.\left\{400-\left[673-2^3.\left(7^8:7^6+7^0\right)\right]\right\}\)

#Toán lớp 6

Hoàng Ninh

27 tháng 3 2018

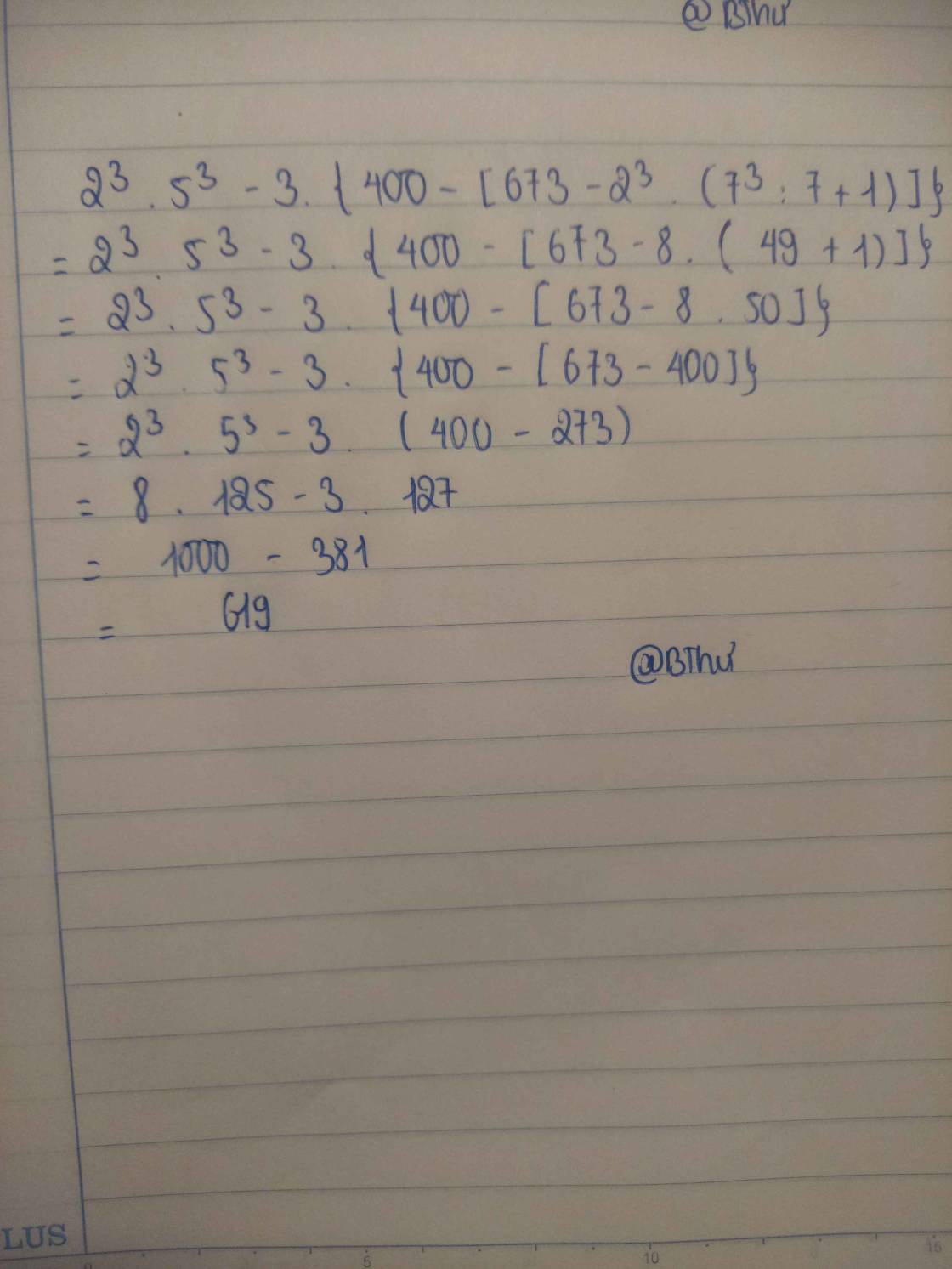
Câu 1:

\(A=\frac{2^5.7+2^5}{2^5.3-2^5}\)= \(\frac{2^5.8}{2^5.2}\)= 4

Vậy A = 4

Câu 2:

\(B=2^3.5^3-3.\left\{400-\left[673-2^3.\left(7^8:7^6+7^0\right)\right]\right\}\)

\(B=8.125-3.\left\{400-\left[673-8.\left(7^2+1\right)\right]\right\}\)

\(B=1000-3.\left\{400-\left[673-8.\left(49+1\right)\right]\right\}\)

\(B=1000-3.\left\{400-\left[673-8.50\right]\right\}\)

\(B=1000-3.\left\{400-\left[673-400\right]\right\}\)

\(B=1000-3.\left\{400-273\right\}\)

\(B=1000-3.127\)

\(B=1000-381\)

\(B=619\)

Vậy B = 619

Đúng(0)

Bang Bang Tan

20 tháng 4 2018 - olm

x/3=2/3+(-1/7)

Mong mọi người trả lời sớm giúp mình nhé!!!!

#Toán lớp 6

songngubenho

20 tháng 4 2018

sao đề kì quá sao mik ko tính ra hay là mik tính sai nhỉ! mik tính được ra là 77 nhưng thuer lại thì thấy kì

Đúng(0)

Trần Cao Vỹ Lượng

20 tháng 4 2018

\(x=\frac{11}{7}\)

Đúng(1)

Lindan0608

9 tháng 3 2019 - olm

Tính: 2³ . 5³ - 3 { 400 - [ 673 - 2³ ( 7⁸ : 7⁶ +7⁰)]}

#Toán lớp 6

Huỳnh Quang Sang

9 tháng 3 2019

\(2^3\cdot5^3-3\left\{400-\left[673-2^3(7^8:7^6+7^0)\right]\right\}\)

\(=8\cdot125-3\left\{400-\left[673-8(7^{8-6}+7^0)\right]\right\}\)

\(=8\cdot125-3\left\{400-\left[673-8(7^2+7^0)\right]\right\}\)

\(=8\cdot125-3\left\{400-\left[673-8(49+1)\right]\right\}\)

\(=8\cdot125-3\left\{400-\left[673-8\cdot50\right]\right\}\)

\(=8\cdot125-3\left\{400-\left[673-400\right]\right\}\)

\(=8\cdot125-3\left\{400-273\right\}\)

\(=8\cdot125-3\cdot127\)

\(=619\)

Đúng(0)

Hoàng Ninh

9 tháng 3 2019

\(2^3.5^3-3\left\{400-\left[673-2^3\left(7^8:7^6+7^0\right)\right]\right\}\)

\(=8.125-3\left\{400-\left[673-8\left(49+1\right)\right]\right\}\)

\(=1000-3\left\{400-\left[673-8.50\right]\right\}\)

\(=1000-3\left\{400-\left[673-400\right]\right\}\)

\(=1000-3\left\{400-273\right\}\)

\(=1000-3.\left(127\right)\)

\(=1000-381\)

\(=619\)

Đúng(0)

Linh Chi

24 tháng 1 2021 - olm

S₂= 1+(-3)+5+(-7)+...+(-1999)+2001

S₃= 1+(-2)+(-3)+4+5+(-6)+(-7)+8+...1997+(-1998)+(-1999)+2002

Mọi người trả lời giúp em với ạ. Em cảm ơn.

#Toán lớp 6

Nguyễn Minh Quang

Giáo viên

24 tháng 1 2021

ta có

\(S_2=\left(1-3\right)+\left(5-7\right)+..+\left(1997-1999\right)+2001\)

ha y \(S_2=-2-2-2..+2001=-2.500+2001=1001\)

\(S_3=\left(1-2-3+4\right)+\left(5-6-7+8\right)+..+\left(1997-1998-1999+2002\right)\)

hay \(S_3=0+0+..+0=0\)

Đúng(0)

Đặng Ngọc Quỳnh

24 tháng 1 2021

\(S_2=\left(1-3\right)+\left(5-7\right)+...+\left(1997-1999\right)+2001\)

\(=\left(-2\right)+\left(-2\right)+....+\left(-2\right)+2001=\left(-2\right).500+2001=-1000+2001=1001\)

\(S_3=\left(0+1-2-3\right)+\left(4+5-6-7\right)+...+\left(1996+1997-1998-1999\right)+2000\)

\(=-4+\left(-4\right)+...+\left(-4\right)+2000=\left(-4\right).500+2000=0\)

Đúng(0)

Phù Dung

7 tháng 3 2018 - olm

Tính: 2³ . 2⁵ - 3 { 400 - [ 673 - 2³ ( 7⁸ : 7⁶ +7⁰)]}

mấy boạn giúp mùn vs, nhóa

#Toán lớp 6

ღღ_๖ۣ nhók_lùn ❣_ღღ

7 tháng 3 2018

2³ . 2⁵ - 3 { 400 - [ 673 - 2³ ( 7⁸ : 7⁶ +7⁰)]}

= 2⁸ - 3 { 400 - [ 673 - 8 ( 7² +1 )]}

= 256 - 3 { 400 - [ 673 - 8 . 50 ]}

= 256 - 3 { 400 - [ 673 - 400 ]}

= 256 - 3 { 400 - 273 }

= 256 - 3 . 127

= 256 - 381

= - 125

Đúng(0)

đoàn thu hằng

11 tháng 4 2019

bằng 619 mới đúng nhé

Đúng(0)

Nguyen Van Do

4 tháng 10 2018 - olm

mọi người giúp mik giải cái mẫu báo cáo lớp 7 bài 6 hộ mink với nha ,hình ko cần vẽ đâu ,ai trả lời hay mik sẽ cho 3 TICK nhưng nhớ là trong đêm nay nhá

#Toán lớp 6

như phương phùng lai

17 tháng 1 2017 - olm

C=1+2+3-4+5+6+7-8+...+1999-2000+2001

Mong mọi người trả lời sơms ạ.

#Toán lớp 6

nguyen bao khanh

6 tháng 1 2018

C=1+2+3-4+5+6+7-8+...+1999-2000+2001

C=1+2+(-1)+5+6+(-1)+...+1997+1998+(-1)+2001

C=1+1+5+5+...+1997+1997+2001

C=2001+(1.2+5.2+...+1997.2)

C=2001+2(1+5+...+1997)

Tong 1+5+...+1997={(1997+1)[(1997-1):4+1]}:2=499500

C=2001+2.499500

C=2001+999000

C=1001001

he he

Đúng(0)

The Scorpion

8 tháng 4 2018 - olm

Thực hiện phép tính ( Tính hợp lý nếu có thể )

a) 1968 : 16 + 5136 : 16 - 704 : 16

b) 2³ x 5³ - 3 {400 - [ 673 - 2³.(7⁸ : 7⁶ + 7⁰)]}

#Toán lớp 6

Untra_Goku

8 tháng 4 2018

\(b,2^3x5^3-3x\left\{400-\left[673-2^3x\left(7^8:7^6+7^0\right)\right]\right\}\)

\(=1000-3x\left\{400-\left[673-8x\left(7^2+1\right)\right]\right\}\)

\(=1000-3x\left\{400-\left[673-8x50\right]\right\}\)

\(=1000-3x\left\{400-\left[673-400\right]\right\}\)

\(=1000-3x\left\{400-273\right\}\)

\(=1000-3x127\)

\(=1000-381\)

\(=619\)

Đúng(0)

Untra_Goku

8 tháng 4 2018

\(a,1968:16+5136:16-704:16\)

\(=\left(1968+5136-704\right):16\)

\(=6400:16\)

\(=400\)

Đúng(0)

Trần Đình Anh

25 tháng 7 2017 - olm

Chứng minh 2^1 + 2^2 +2^3 + 2^4 +.....+2^2010. chia hết cho 3 và 7 ( ^ là dấu mũ nhé). Chứng minh 3^1 + 3^2 + 3^3 +.......+ 3^2010 chia hết cho 4 và 13Chứng minh 5^1 + 5^2 + 5^3 + ........ + 5^2010 chia hết cho 6 và 31Chứng minh 7^1 + 7^2 + 7^3 + .....+ 7^2010 chia hết cho 8 và 57Mọi người chỉ trả lời một phần cũng ok thank mn...

Đọc tiếp

#Toán lớp 6

Nguyễn Thùy Linh

25 tháng 7 2017

1. Ta có: A = 2^1+ 2^2 +2^3+2^4+....2^10

A= ( 2^1 + 2^2) + ( 2^3+2^4) +....( 2^9+ 2^10)

A= 3.( 2^1+2^3+2^5+...+2^1005)

Do 3 \(⋮\)3 => A\(⋮\)3

Ta có: A =.....

A= Ghép 3 số lại

A= 7. (2^1+ 2^4+...+2^670)

Do 7 \(⋮\)7 => A \(⋮\)7

2;3;4 đều ghép 2 hoặc 3 số như tke và phần trog ngoặc cx y hệt như tke, ko thay đổi

Duyệt nhanh....

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP