Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
*) Ta có: AC // Ox
Oy cắt AC tại C, cắt Ox tại O
Từ hai điều trên suy ra: \(\widehat{xOy}\)và \(\widehat{ACy}\)là 2 góc đồng vị bằng nhau
Mà \(\widehat{xOy}\)= \(70^o\)=> \(\widehat{ACy}\)= \(70^o\)
*) Ta có: BA // Oy
AC cắt BA tại A, cắt Oy tại C
Từ 2 điều trên suy ra: \(\widehat{ACy}=\widehat{DAz}\)(2 góc đồng vị bằng nhau)
=> \(\widehat{DAz}\)= \(70^o\)
Ta có: \(\widehat{DAz}\)và \(\widehat{BAC}\)là 2 góc đối đỉnh
=> \(\widehat{BAC}\)= \(70^o\)
Ta có: \(\widehat{BAC}\)+ \(\widehat{CAz}=180^o\)(2 góc kề bù)
=> \(\widehat{CAz}=110^o\)
Mà \(\widehat{CAz}\)và \(\widehat{BAD}\)là 2 góc đối đỉnh => \(\widehat{BAD}\)= \(110^o\)
Vậy...

a) Gọi G, F lần lượt là chân đường vuông góc từ O kẻ xuống AB và AC
Ta có: O nằm trên đường trung trực của AB(gt)
mà OG⊥AB(gt)
nên G là trung điểm của AB
Ta có: O nằm trên đường trung trực của AC(gt)
mà OF⊥AC(gt)
nên F là trung điểm của AC
Ta có: \(AG=\dfrac{AB}{2}\)(G là trung điểm của AB)
\(AF=\dfrac{AC}{2}\)(F là trung điểm của AC)
mà AB=AC(ΔABC cân tại A)
nên AG=AF
Xét ΔAGO vuông tại G và ΔAFO vuông tại F có
AO chung
AG=AF(cmt)
Do đó: ΔAGO=ΔAFO(cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{GAO}=\widehat{FAO}\)(hai góc tương ứng)
hay \(\widehat{BAO}=\widehat{CAO}\)
mà tia AO nằm giữa hai tia AB,AC
nên AO là tia phân giác của \(\widehat{BAC}\)(đpcm)
c) Xét ΔAOB và ΔAOC có
AB=AC(ΔABC cân tại A)
\(\widehat{BAO}=\widehat{CAO}\)(cmt)
AO chung
Do đó: ΔAOB=ΔAOC(c-g-c)
Suy ra: OB=OC(hai cạnh tương ứng)
Ta có: \(\widehat{ABC}+\widehat{KBC}=\widehat{ABK}\)(tia BC nằm giữa hai tia BA,BK)
nên \(\widehat{ABC}+\widehat{KBC}=90^0\)(1)
Ta có: \(\widehat{ACB}+\widehat{KCB}=\widehat{ACK}\)(tia CB nằm giữa hai tia CA,CK)
nên \(\widehat{ACB}+\widehat{KCB}=90^0\)(2)
Từ (1) và (2) suy ra \(\widehat{ABC}+\widehat{KBC}=\widehat{ACB}+\widehat{KCB}\)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{KBC}=\widehat{KCB}\)
Xét ΔKBC có \(\widehat{KBC}=\widehat{KCB}\)(cmt)
nên ΔKBC cân tại K(Định lí đảo của tam giác cân)
Suy ra: KB=KC(hai cạnh bên)
Xét ΔBEC vuông tại E và ΔCDB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔBEC=ΔCDB(cạnh huyền-góc nhọn)
Suy ra: \(\widehat{BCE}=\widehat{CBD}\)(hai góc tương ứng)
hay \(\widehat{HBC}=\widehat{HCB}\)
Xét ΔHBC có \(\widehat{HBC}=\widehat{HCB}\)(cmt)
nên ΔHBC cân tại H(Định lí đảo của tam giác cân)
Suy ra: HB=HC(hai cạnh bên)
Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(3)
Ta có: OB=OC(cmt)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(4)
Ta có: HB=HC(cmt)
nên H nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(5)
Ta có: KB=KC(cmt)
nên K nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(6)
Từ (3), (4), (5) và (6) suy ra A,O,H,K thẳng hàng(đpcm)

a) Gọi G, F lần lượt là chân đường vuông góc từ O kẻ xuống AB và AC
Ta có: O nằm trên đường trung trực của AB(gt)
mà OG⊥AB(gt)
nên G là trung điểm của AB
Ta có: O nằm trên đường trung trực của AC(gt)
mà OF⊥AC(gt)
nên F là trung điểm của AC
Ta có: AG=AB2AG=AB2(G là trung điểm của AB)
AF=AC2AF=AC2(F là trung điểm của AC)
mà AB=AC(ΔABC cân tại A)
nên AG=AF
Xét ΔAGO vuông tại G và ΔAFO vuông tại F có
AO chung
AG=AF(cmt)
Do đó: ΔAGO=ΔAFO(cạnh huyền-cạnh góc vuông)
Suy ra: ˆGAO=ˆFAOGAO^=FAO^(hai góc tương ứng)
hay ˆBAO=ˆCAOBAO^=CAO^
mà tia AO nằm giữa hai tia AB,AC
nên AO là tia phân giác của ˆBACBAC^(đpcm)
c) Xét ΔAOB và ΔAOC có
AB=AC(ΔABC cân tại A)
ˆBAO=ˆCAOBAO^=CAO^(cmt)
AO chung
Do đó: ΔAOB=ΔAOC(c-g-c)
Suy ra: OB=OC(hai cạnh tương ứng)
Ta có: ˆABC+ˆKBC=ˆABKABC^+KBC^=ABK^(tia BC nằm giữa hai tia BA,BK)
nên ˆABC+ˆKBC=900ABC^+KBC^=900(1)
Ta có: ˆACB+ˆKCB=ˆACKACB^+KCB^=ACK^(tia CB nằm giữa hai tia CA,CK)
nên ˆACB+ˆKCB=900ACB^+KCB^=900(2)
Từ (1) và (2) suy ra ˆABC+ˆKBC=ˆACB+ˆKCBABC^+KBC^=ACB^+KCB^
mà ˆABC=ˆACBABC^=ACB^(hai góc ở đáy của ΔABC cân tại A)
nên ˆKBC=ˆKCBKBC^=KCB^
Xét ΔKBC có ˆKBC=ˆKCBKBC^=KCB^(cmt)
nên ΔKBC cân tại K(Định lí đảo của tam giác cân)
Suy ra: KB=KC(hai cạnh bên)
Xét ΔBEC vuông tại E và ΔCDB vuông tại D có
BC chung
ˆEBC=ˆDCBEBC^=DCB^(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔBEC=ΔCDB(cạnh huyền-góc nhọn)
Suy ra: ˆBCE=ˆCBDBCE^=CBD^(hai góc tương ứng)
hay ˆHBC=ˆHCBHBC^=HCB^
Xét ΔHBC có ˆHBC=ˆHCBHBC^=HCB^(cmt)
nên ΔHBC cân tại H(Định lí đảo của tam giác cân)
Suy ra: HB=HC(hai cạnh bên)
Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(3)
Ta có: OB=OC(cmt)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(4)
Ta có: HB=HC(cmt)
nên H nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(5)
Ta có: KB=KC(cmt)
nên K nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(6)
Từ (3), (4), (5) và (6) suy ra A,O,H,K thẳng hàng(đpcm)

Kẻ `KI ⊥ BC(I in BC)`
Đặt `BG` là p/g của góc ngoài tại `hat(ABC)`
`CH` là p/g của góc ngoài tại `hat(ACB)`
+, Có : `BG` là p/g của góc ngoài tại `hat(ABC)`
`=>hat(B_1)=hat(B_2)`
mà `hat(B_1)=hat(B_3);hat(B_2)=hat(B_4)` ( đối đỉnh )
nên `hat(B_3)=hat(B_4)`
+, Có : `CH` là p/g của góc ngoài tại `hat(ACB)`
`=>hat(C_1)=hat(C_2)`
mà `hat(C_1)=hat(C_3);hat(C_2)=hat(C_4)` ( đối đỉnh )
nên `hat(C_3)=hat(C_4)`
Xét `Delta BEK` và `Delta BIK` có :
`{:(hat(F)=hat(I_1)(=90^0)),(KB-chung),(hat(B_3)=hat(B_4)(cmt)):}}`
`=>Delta BEK=Delta BIK(c.h-g.n)`
`=>KE=KI` ( 2 cạnh t/ứng ) (1)
Xét `Delta KIC` và `Delta KEC` có :
`{:(hat(I_2)=hat(E)(=90^0)),(KC-xhung),(hat(C_3)=hat(C_4)(cmt)):}}`
`=>Delta KIC=Delta KEC(c.h-g.n)`
`=> KI=KE` ( 2 cạnh t/ứng ) (2)
Từ (1) và (2) `=>KF=KE(=KI)(đpcm)`
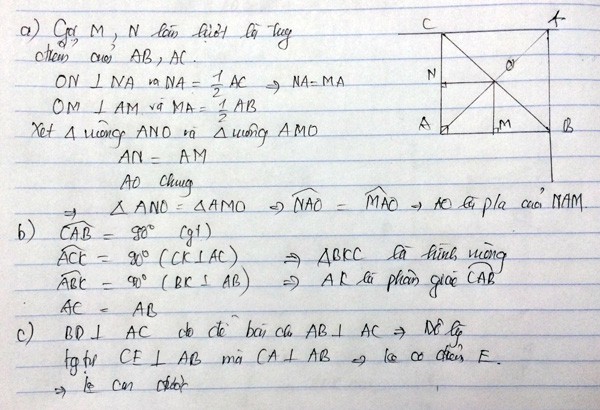
Tứ giác ABKC có
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{K}=360^0\)
\(\Rightarrow\widehat{K}=360^o-70^o-90^o-90^o\)
\(\Rightarrow\widehat{K}=110^o\)
Vậy \(\widehat{BKC}=110^0\)