Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(4-\sqrt{7}\right)^2=4^2-2\cdot4\cdot\sqrt{7}+7\)
\(=16-8\sqrt{7}+7=23-8\sqrt{7}\)
\(\sqrt{9-4\sqrt{5}}-\sqrt{5}\)
\(=\sqrt{5-2\cdot\sqrt{5}\cdot2+4}-\sqrt{5}\)
\(=\sqrt{\left(\sqrt{5}-2\right)^2}-\sqrt{5}\)
\(=\left|\sqrt{5}-2\right|-\sqrt{5}\)
\(=\sqrt{5}-2-\sqrt{5}=-2\)
\(\dfrac{\sqrt{4-2\sqrt{3}}}{1+\sqrt{2}}:\dfrac{\sqrt{2}-1}{\sqrt{3}+1}\)
\(=\dfrac{\sqrt{3-2\cdot\sqrt{3}\cdot1+1}}{\sqrt{2}+1}\cdot\dfrac{\sqrt{3}+1}{\sqrt{2}-1}\)
\(=\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{2}+1}\cdot\dfrac{\sqrt{3}+1}{\sqrt{2}-1}\)
\(=\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}=\dfrac{3-1}{2-1}=2\)
\(\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}-\dfrac{6\sqrt{6}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{1}{2}\sqrt{6}-2\sqrt{6}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\dfrac{1}{2}-2=-\dfrac{3}{2}=-1,5\)

`c)root{3}{4}.root{3}{1-sqrt3}.root{6}{(sqrt3+1)^2}`
`=root{3}{4(1-sqrt3)}.root{3}{1+sqrt3}`
`=root{3}{4(1-sqrt3)(1+sqrt3)}`
`=root{3}{4(1-3)}=-2`
`d)2/(root{3}{3}-1)-4/(root{9}-root{3}{3}+1)`
`=(2(root{3}{9}+root{3}{3}+1))/(3-1)-(4(root{3}{3}+1))/(3+1)`
`=root{3}{9}+root{3}{3}+1-root{3}{3}-1`
`=root{3}{9}`
`a)root{3}{8sqrt5-16}.root{3}{8sqrt5+16}`
`=root{3}{(8sqrt5-16)(8sqrt5+16)}`
`=root{3}{320-256}`
`=root{3}{64}=4`
`b)root{3}{7-5sqrt2}-root{6}{8}`
`=root{3}{1-3.sqrt{2}+3.2.1-2sqrt2}-root{6}{(2)^3}`
`=root{3}{(1-sqrt2)^3}-sqrt2`
`=1-sqrt2-sqrt2=1-2sqrt2`

\(1.\text{ }\dfrac{1}{\sqrt{k}-\sqrt{k+1}}=\dfrac{\left(\sqrt{k}+\sqrt{k+1}\right)}{\left(\sqrt{k}+\sqrt{k+1}\right)\left(\sqrt{k}-\sqrt{k+1}\right)}\\ =-\left(\sqrt{k}+\sqrt{k+1}\right)\\ \Rightarrow\dfrac{1}{\sqrt{1}-\sqrt{2}}-\dfrac{1}{\sqrt{2}-\sqrt{3}}+\dfrac{1}{\sqrt{3}-\sqrt{4}}-...-\dfrac{1}{\sqrt{8}-\sqrt{9}}\\ =-\left(\sqrt{1}+\sqrt{2}\right)+\left(\sqrt{2}+\sqrt{3}\right)-\left(\sqrt{3}+\sqrt{4}\right)+...+\left(\sqrt{8}+\sqrt{9}\right)\\ =-\sqrt{1}-\sqrt{2}+\sqrt{2}+\sqrt{3}-\sqrt{3}-\sqrt{4}+...+\sqrt{8}+\sqrt{9}\\ \\ =\sqrt{9}-\sqrt{1}=2\)
\(2.\text{ }\dfrac{1}{\left(k+1\right)\sqrt{k}+\sqrt{k+1}k}=\dfrac{1}{\sqrt{k\left(k+1\right)}\left(\sqrt{k+1}+\sqrt{k}\right)}\\ =\dfrac{\sqrt{k+1}-\sqrt{k}}{\sqrt{k\left(k+1\right)}\left(\sqrt{k+1}+\sqrt{k}\right)\left(\sqrt{k+1}-\sqrt{k}\right)}\\ =\dfrac{\sqrt{k+1}-\sqrt{k}}{\sqrt{k\left(k+1\right)}\left(k+1-k\right)}=\dfrac{\sqrt{k+1}-\sqrt{k}}{\sqrt{k\left(k+1\right)}}\\ =\dfrac{1}{\sqrt{k}}-\dfrac{1}{\sqrt{k+1}}\\ \Rightarrow\text{ }\dfrac{1}{2\sqrt{1}+1\sqrt{2}}+\dfrac{1}{3\sqrt{2}+2\sqrt{3}}+...+\dfrac{1}{7\sqrt{6}+6\sqrt{7}}\\ =\text{ }\dfrac{1}{\sqrt{1}}-\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{2}}-\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{6}}-\dfrac{1}{\sqrt{7}}\\ =\text{ }\dfrac{1}{\sqrt{1}}-\dfrac{1}{\sqrt{7}}\\ \text{ }1-\dfrac{1}{\sqrt{7}}\)
1.\(\dfrac{1}{\sqrt{1}-\sqrt{2}}-\dfrac{1}{\sqrt{2}-\sqrt{3}}+\dfrac{1}{\sqrt{3}-\sqrt{4}}-\dfrac{1}{\sqrt{4}-\sqrt{5}}+\dfrac{1}{\sqrt{5}-\sqrt{6}}-\dfrac{1}{\sqrt{6}-\sqrt{7}}+\dfrac{1}{\sqrt{7}-\sqrt{8}}-\dfrac{1}{\sqrt{8}-\sqrt{9}}=\dfrac{1+\sqrt{2}}{1-2}-\dfrac{\sqrt{2}+\sqrt{3}}{2-3}+\dfrac{\sqrt{3}+\sqrt{4}}{3-4}-\dfrac{\sqrt{4}+\sqrt{5}}{4-5}+\dfrac{\sqrt{5}+\sqrt{6}}{5-6}-\dfrac{\sqrt{6}+\sqrt{7}}{6-7}+\dfrac{\sqrt{7}+\sqrt{8}}{7-8}-\dfrac{\sqrt{8}+\sqrt{9}}{8-9}=-1-\sqrt{2}+\sqrt{2}+\sqrt{3}-\sqrt{3}-\sqrt{4}+\sqrt{4}+\sqrt{5}-\sqrt{5}-\sqrt{6}+\sqrt{6}+\sqrt{7}-\sqrt{7}-\sqrt{8}+\sqrt{8}+\sqrt{9}=\sqrt{9}-1=3-1=2\)

6:ĐKXĐ: x>=0; x<>1/25
BPT=>\(\dfrac{3\sqrt{x}}{5\sqrt{x}-1}+3< =0\)
=>\(\dfrac{3\sqrt{x}+15\sqrt{x}-5}{5\sqrt{x}-1}< =0\)
=>\(\dfrac{18\sqrt{x}-5}{5\sqrt{x}-1}< =0\)
=>\(\dfrac{1}{5}< \sqrt{x}< =\dfrac{5}{18}\)
=>\(\dfrac{1}{25}< x< =\dfrac{25}{324}\)
7:
ĐKXĐ: x>=0
BPT \(\Leftrightarrow\dfrac{\sqrt{x}+1}{2\sqrt{x}+3}>\dfrac{8}{3}:\dfrac{8}{3}=1\)
=>\(\dfrac{\sqrt{x}+1}{2\sqrt{x}+3}-1>=0\)
=>\(\dfrac{\sqrt{x}+1-2\sqrt{x}-3}{2\sqrt{x}+3}>=0\)
=>\(-\sqrt{x}-2>=0\)(vô lý)
8:
ĐKXĐ: x>=0; x<>9/4
BPT \(\Leftrightarrow\dfrac{\sqrt{x}-2}{2\sqrt{x}-3}+4< 0\)
=>\(\dfrac{\sqrt{x}-2+8\sqrt{x}-12}{2\sqrt{x}-3}< 0\)
=>\(\dfrac{9\sqrt{x}-14}{2\sqrt{x}-3}< 0\)
TH1: 9căn x-14>0 và 2căn x-3<0
=>căn x>14/9 và căn x<3/2
=>14/9<căn x<3/2
=>196/81<x<9/4
TH2: 9căn x-14<0 và 2căn x-3>0
=>căn x>3/2 hoặc căn x<14/9
mà 3/2<14/9
nên trường hợp này Loại
9:
ĐKXĐ: x>=0
\(BPT\Leftrightarrow\dfrac{2\sqrt{x}+3}{5\sqrt{x}+7}< =-\dfrac{1}{3}\)
=>\(\dfrac{2\sqrt{x}+3}{5\sqrt{x}+7}+\dfrac{1}{3}< =0\)
=>\(\dfrac{6\sqrt{x}+9+5\sqrt{x}+7}{3\left(5\sqrt{x}+7\right)}< =0\)
=>\(\dfrac{11\sqrt{x}+16}{3\left(5\sqrt{x}+7\right)}< =0\)(vô lý)
10:
ĐKXĐ: x>=0; x<>1/49
\(BPT\Leftrightarrow\dfrac{6\sqrt{x}-2}{7\sqrt{x}-1}+6>0\)
=>\(\dfrac{6\sqrt{x}-2+42\sqrt{x}-6}{7\sqrt{x}-1}>0\)
=>\(\dfrac{48\sqrt{x}-8}{7\sqrt{x}-1}>0\)
=>\(\dfrac{6\sqrt{x}-1}{7\sqrt{x}-1}>0\)
TH1: 6căn x-1>0 và 7căn x-1>0
=>căn x>1/6 và căn x>1/7
=>căn x>1/6
=>x>1/36
TH2: 6căn x-1<0 và 7căn x-1<0
=>căn x<1/6 và căn x<1/7
=>căn x<1/7
=>0<=x<1/49

a) Ta có: \(\sqrt{3-2\sqrt{2}}-\sqrt{11+6\sqrt{2}}\)
\(=\sqrt{2}-1-3-\sqrt{2}\)
=-4
b) Ta có: \(\sqrt{4-2\sqrt{3}}-\sqrt{7-4\sqrt{3}}+\sqrt{19+8\sqrt{3}}\)
\(=\sqrt{3}-1-2+\sqrt{3}+4+\sqrt{3}\)
\(=3\sqrt{3}+1\)
c) Ta có: \(\sqrt{6-2\sqrt{5}}+\sqrt{9+4\sqrt{5}}-\sqrt{14-6\sqrt{5}}\)
\(=\sqrt{5}-1+\sqrt{5}-2-3+\sqrt{5}\)
\(=3\sqrt{5}-6\)
d) Ta có: \(\sqrt{11-4\sqrt{7}}+\sqrt{23-8\sqrt{7}}+\sqrt{\left(-2\right)^6}\)
\(=\sqrt{7}-2+4-\sqrt{7}+8\)
=10

\(A=-\sqrt{2}-\sqrt{1}+\sqrt{2}+\sqrt{3}-\sqrt{3}-\sqrt{4}+....-\sqrt{7}-\sqrt{8}+\sqrt{8}+\sqrt{9}\)
\(A=\sqrt{9}-\sqrt{1}=3-1=2\)
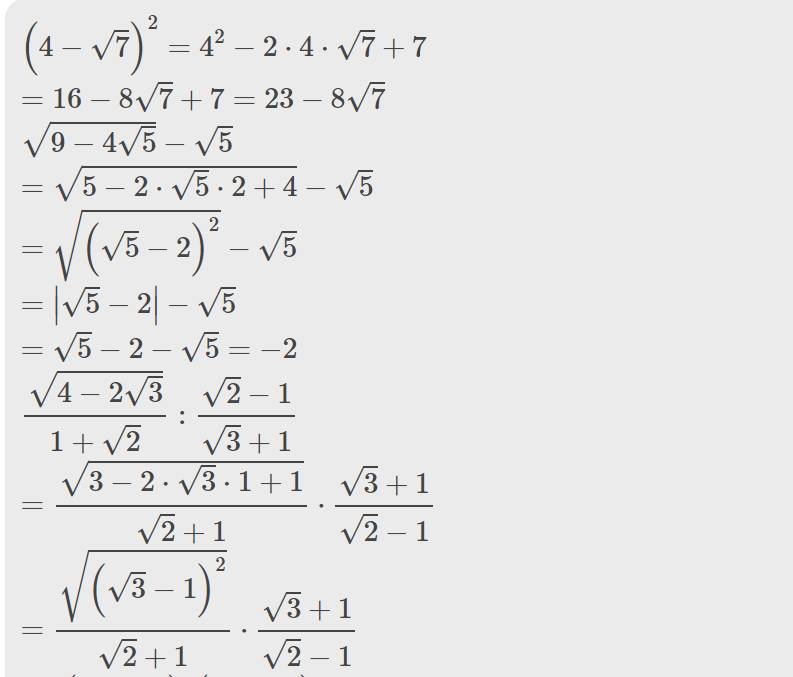
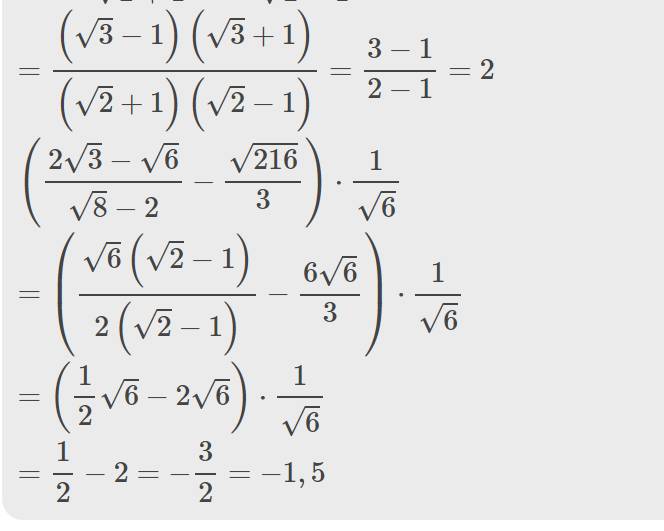
tách 11 ra thành \(\sqrt{3}\) mũ 2 + căn 8 mũ 2
áp dụng hẳng đẳng thức đáng nhớ A^2+2AB +B^2=(A+B)^2
vào \(\sqrt{11+4\sqrt{6}}\)
.Bản thử đi nhé kết quả của mình là \(\sqrt{3}\)+\(\sqrt{8}\)
Vì ko gõ đc căn nên mình ko giải hẳn hoi ra đc .Bạn thông cảm ha.
Chúc bn hok tốt!
Nguyễn Duy Phương ngại viếết lắm căn quá
bạn có quyển nâng cao và phát triểển toán 9 ko Tập 1 ý .Trong đó có đầy đủ.Còn không có thì bạn cứ làm tương tự câu a.