Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(=\dfrac{x^3-1}{x+2}\cdot\dfrac{x^2+x+1-x^2+1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x+2}{x+2}=1\)
b: \(=\dfrac{\left(x+2\right)\left(x-1\right)\left(x+1\right)}{2\left(x+5\right)}\cdot\left(\dfrac{x+1-2x+2}{\left(x-1\right)\left(x+1\right)}+\dfrac{1}{x+2}\right)\)
\(=\dfrac{\left(x+2\right)\left(x-1\right)\left(x+1\right)}{2\left(x+5\right)}\cdot\left(\dfrac{-\left(x-3\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{1}{x+2}\right)\)
\(=\dfrac{\left(x+2\right)\left(x-1\right)\left(x+1\right)}{2\left(x+5\right)}\cdot\dfrac{-\left(x^2-x-6\right)+x^2-1}{\left(x-1\right)\left(x+1\right)\left(x+2\right)}\)
\(=\dfrac{-x^2+x+6+x^2-1}{2\left(x+5\right)}=\dfrac{x+5}{2\left(x+5\right)}=\dfrac{1}{2}\)

\(a,=\dfrac{4y.5x^3}{3x^2.2y^3}=\dfrac{20x^3y}{6x^2y^3}=\dfrac{10x}{3y^2}\\ b,=\dfrac{\left(x-1\right)^2.x\left(x+1\right)}{\left(x-1\right)\left(x+1\right)\left(x-1\right)}=\dfrac{\left(x-1\right)^2.x.\left(x+1\right)}{\left(x-1\right)^2.\left(x+1\right)}=x\)
\(c,=\dfrac{x\left(2+x\right).3\left(x^3+1\right)}{\left(x^2-x+1\right).3.\left(x+2\right)}=\dfrac{3x.\left(x+2\right).\left(x+1\right)\left(x^2-x+1\right)}{\left(x^2-x+1\right).3\left(x+2\right)}=x\left(x+1\right)\)

\(a,\dfrac{x^2+2}{x^3+1}-\dfrac{1}{x+1}\left(ĐKXĐ:x\ne-1\right)\\ =\dfrac{x^2+2-\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}\\ =\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\\ c,\dfrac{1}{2-2x}-\dfrac{3}{2+2x}+\dfrac{2x}{x^2-1}\\ =\dfrac{-1}{2\left(x-1\right)}-\dfrac{3}{2\left(x+1\right)}+\dfrac{2x}{\left(x-1\right)\left(x+1\right)}\left(ĐKXĐ:x\ne\pm1\right)\\ =\dfrac{-1\left(x+1\right)-3\left(x-1\right)+2x.2}{2\left(x+1\right)\left(x-1\right)}\\ =\dfrac{-x-1-3x+3+4x}{2\left(x+1\right)\left(x-1\right)}=\dfrac{2}{2\left(x+1\right)\left(x-1\right)}=\dfrac{1}{\left(x-1\right)\left(x+1\right)}\)

`a, a/(a-3) - 3/(a+3) = (a(a+3) - 3(a-3))/(a^2-9)`
`= (a^2+9)/(a^2-9)`
`b, 1/(2x) + 2/x^2 = x/(2x^2) + 4/(2x^2) = (x+4)/(2x^2)`
`c, 4/(x^2-1) - 2/(x^2+x) = (4x)/(x(x-1)(x+1)) - (2(x-1))/(x(x+1)(x-1))`
`= (2x+2)/(x(x-1)(x+1)`
`= 2/(x(x-1))`

a: |2x-3|=1
=>2x-3=1 hoặc 2x-3=-1
=>x=1(nhận) hoặc x=2(loại)
KHi x=1 thì \(A=\dfrac{1+1^2}{2-1}=2\)
b: ĐKXĐ: x<>-1; x<>2
\(B=\dfrac{2x^2-4x+3x+3-2x^2-1}{\left(x-2\right)\left(x+1\right)}=\dfrac{-x+2}{\left(x-2\right)\left(x+1\right)}=\dfrac{-1}{x+1}\)

a: \(\dfrac{x}{2x^2+7x-15}=\dfrac{x}{\left(x+5\right)\left(2x-3\right)}=\dfrac{x^2-2x}{\left(x+5\right)\left(x-2\right)\left(2x-3\right)}\)
\(\dfrac{x+2}{x^2+3x-10}=\dfrac{x+2}{\left(x+5\right)\left(x-2\right)}=\dfrac{\left(x+2\right)\left(2x-3\right)}{\left(2x-3\right)\left(x+5\right)\left(x-2\right)}\)
\(\dfrac{1}{x+5}=\dfrac{\left(2x-3\right)\left(x-2\right)}{\left(2x-3\right)\left(x-2\right)\left(x+5\right)}\)
b: \(\dfrac{1}{-x^2+3x-2}=\dfrac{-1}{\left(x-1\right)\left(x-2\right)}=\dfrac{-\left(x+6\right)\left(x-3\right)}{\left(x-1\right)\left(x-2\right)\left(x+6\right)\left(x-3\right)}\)
\(\dfrac{1}{x^2+5x-6}=\dfrac{1}{\left(x+6\right)\left(x-1\right)}=\dfrac{\left(x-2\right)\left(x-3\right)}{\left(x+6\right)\left(x-1\right)\left(x-2\right)\left(x-3\right)}\)
\(\dfrac{1}{-x^2+4x-3}=\dfrac{-1}{\left(x-1\right)\left(x-3\right)}=\dfrac{-\left(x-2\right)\left(x+6\right)}{\left(x-1\right)\left(x-3\right)\left(x+6\right)\left(x-2\right)}\)
c: \(\dfrac{3}{x^3-1}=\dfrac{3}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(\dfrac{2x}{x^2+x+1}=\dfrac{2x\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(\dfrac{x}{x-1}=\dfrac{x\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)

a,\(\dfrac{3-x}{x-5}+\dfrac{2x-8}{x-5}=\dfrac{3-x+2x-8}{x-5}=\dfrac{x-5}{x-5}=1\)
b, \(\dfrac{1}{x-y}+\dfrac{1}{x+y}+\dfrac{2x}{x^2-y^2}=\dfrac{x+y}{\left(x-y\right)\left(x+y\right)}+\dfrac{x-y}{\left(x-y\right)\left(x+y\right)}+\dfrac{2x}{\left(x-y\right)\left(x+y\right)}=\dfrac{x+y+x-y+2x}{\left(x-y\right)\left(x+y\right)}=\dfrac{4x}{\left(x-y\right)\left(x+y\right)}\)

`a,` Với `x=3`
\(B=\dfrac{x^2-x}{2x+1}\\ \Rightarrow\dfrac{3^2-3}{2\cdot3+1}\\ =\dfrac{9-3}{6+1}\\ =\dfrac{6}{7}\)
`b,` Ta có `M=A*B`
\(M=\left(\dfrac{1}{x-1}+\dfrac{x}{x^2-1}\right)\cdot\dfrac{x^2-x}{2x+1}\\ =\left(\dfrac{1}{x-1}+\dfrac{x}{\left(x-1\right)\left(x+1\right)}\right)\cdot\dfrac{x\left(x-1\right)}{2x+\text{ }1}\\ =\left(\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}+\dfrac{x}{\left(x-1\right)\left(x+1\right)}\right)\cdot\dfrac{x\left(x-1\right)}{2x+1}\\ =\dfrac{x+1+x}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x\left(x-1\right)}{2x+1}\\ =\dfrac{2x+1}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x\left(x-1\right)}{2x+1}\\ =\dfrac{x}{x+1}\)
`c,` Để `M=1/2`
`=> x/(x+1)=1/3`
`<=> (3x)/(3(x+1))= (x+1)/(3(x+1))`
`<=> 3x=x+1`
`<=>3x-x=1`
`<=>2x=1`
`<=>x=1/2`
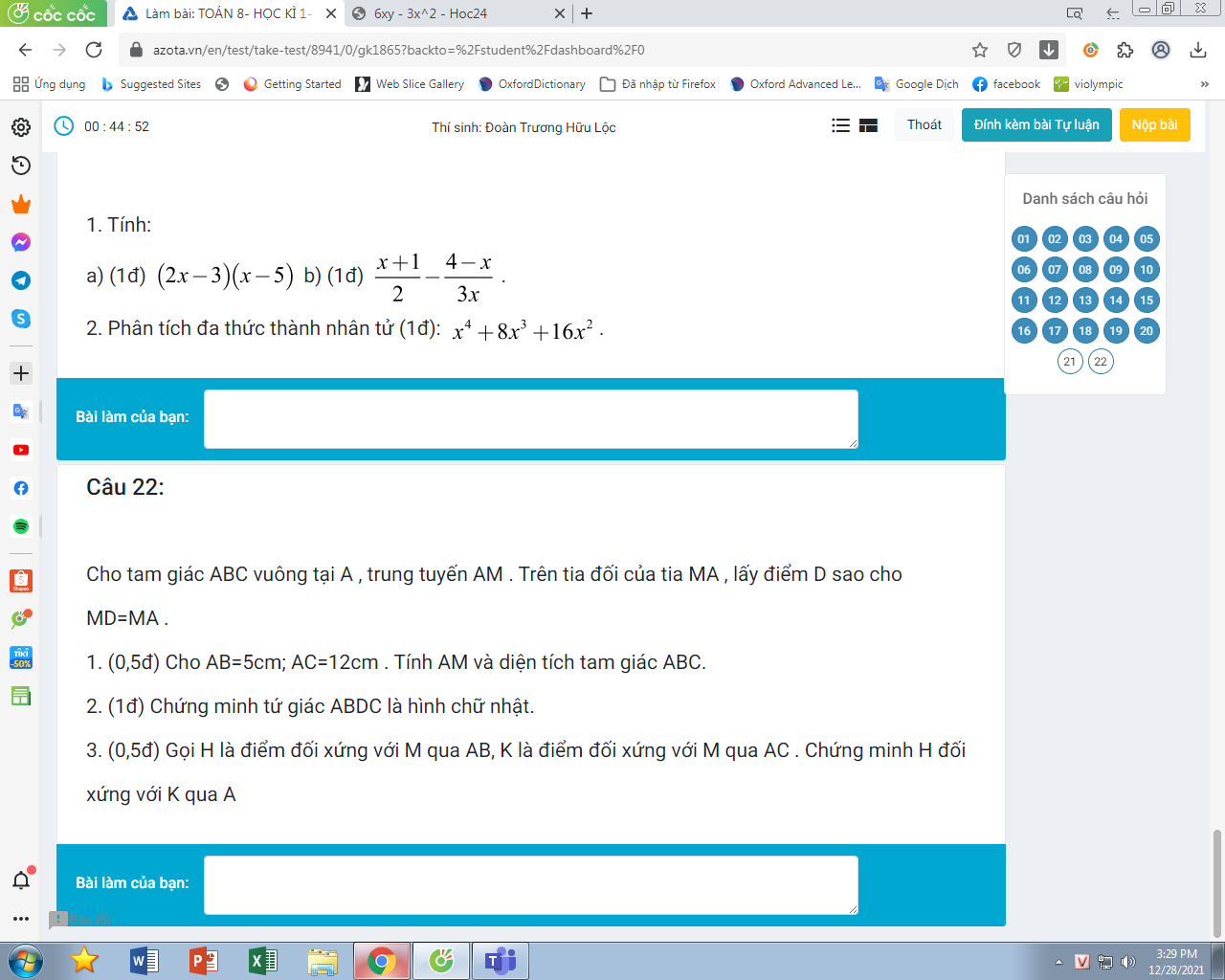
Bài 2:
a: ĐKXĐ: \(x\notin\left\{0;-1\right\}\)
\(\dfrac{1+x}{x+1}-\dfrac{x-1}{x^2+x}\)
\(=\dfrac{x\left(x+1\right)-x+1}{x\left(x+1\right)}\)
\(=\dfrac{x^2+x-x+1}{x^2+x}=\dfrac{x^2+1}{x^2+x}\)
b: ĐKXĐ: \(x\notin\left\{-23;1\right\}\)
\(\dfrac{2x}{x+23}\cdot\dfrac{3x}{x-1}+\dfrac{2x}{x+23}\cdot\dfrac{23-2x}{x-1}\)
\(=\dfrac{2x}{x+23}\cdot\left(\dfrac{3x}{x-1}+\dfrac{23-2x}{x-1}\right)\)
\(=\dfrac{2x}{x+23}\cdot\dfrac{3x+23-2x}{x-1}\)
\(=\dfrac{2x}{x+23}\cdot\dfrac{x+23}{x-1}=\dfrac{2x}{x-1}\)
Bài 3:
a: Sửa đề: AMCN
Ta có: ABCD là hình bình hành
=>BC=AD(1)
Ta có: M là trung điểm của BC
=>\(BM=MC=\dfrac{BC}{2}\left(2\right)\)
Ta có: N là trung điểm của AD
=>\(NA=ND=\dfrac{AD}{2}\left(3\right)\)
Từ (1),(2),(3) suy ra BM=MC=NA=ND
Xét tứ giác AMCN có
MC//AN
MC=AN
Do đó: AMCN là hình bình hành
b: Xét tứ giác ABMN có
BM//AN
BM=AN
Do đó: ABMN là hình bình hành
Hình bình hành ABMN có \(AB=BM\left(=\dfrac{BC}{2}\right)\)
nên ABMN là hình thoi
c: Ta có: BM//AD
=>\(\widehat{EBM}=\widehat{EAD}\)(hai góc đồng vị)
=>\(\widehat{EBM}=60^0\)
Xét ΔBEM có BE=BM(=BA) và \(\widehat{EBM}=60^0\)
nên ΔBEM đều
=>\(\widehat{BEM}=60^0\)
Xét hình thang ANME có \(\widehat{MEA}=\widehat{EAN}=60^0\)
nên ANME là hình thang cân
=>AM=NE