Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(\left\{{}\begin{matrix}n_{H_2}=a\left(mol\right)\\n_{C_nH_{2n-2}}=b\left(mol\right)\end{matrix}\right.\)
=> \(a+b=\dfrac{5,6}{22,4}=0,25\)
\(n_{H_2O}=\dfrac{6,3}{18}=0,35\left(mol\right)\)
\(n_{O_2}=\dfrac{10,64}{22,4}=0,475\left(mol\right)\)
Bảo toàn O: \(n_{CO_2}=\dfrac{0,475.2-0,35}{2}=0,3\left(mol\right)\)
Bảo toàn C: \(b=\dfrac{0,3}{n}\left(mol\right)\) => \(a=0,25-\dfrac{0,3}{n}\)
Bảo toàn H: \(2a+2b\left(n-1\right)=0,7\)
=> n = 3
=> CTPT: C3H4

a) Gọi \(\left\{{}\begin{matrix}n_{CO_2}=a\left(mol\right)\\n_{H_2O}=b\left(mol\right)\end{matrix}\right.\)
=> 44a + 18b = 41,7 (1)
Bảo toàn C: nC = a (mol)
Bảo toàn H: nH = 2b (mol)
=> 12a + 2b = 8,9 (2)
(1)(2) => a = 0,6 (mol); b = 0,85 (mol)
Bảo toàn O: \(n_{O_2}=\dfrac{0,6.2+0,85}{2}=1,025\left(mol\right)\)
=> V = 1,025.22,4 = 22,96 (l)
b) Do \(n_{CO_2}< n_{H_2O}\)
=> 2 hidrocacbon là ankan
nankan = 0,85 - 0,6 = 0,25 (mol)
=> \(\overline{C}=\dfrac{0,6}{0,25}=2,4\)
=> 2 ankan là C2H6 và C3H8

a) \(n_{O_2}=\dfrac{21,28}{22,4}=0,95\left(mol\right)\)
\(n_{CaCO_3}=\dfrac{60}{100}=0,6\left(mol\right)\)
=> nCO2 = 0,6 (mol)
Bảo toàn O: \(n_{H_2O}=0,95.2-0,6.2=0,7\left(mol\right)\)
mdd giảm = \(m_{CaCO_3}-m_{CO_2}-m_{H_2O}=60-0,6.44-0,7.18=21\left(g\right)\)
b) \(n_X=n_{H_2O}-n_{CO_2}=0,7-0,6=0,1\left(mol\right)\)
=> nY = \(\dfrac{5,6}{22,4}-0,1=0,15\left(mol\right)\)
Theo ĐLBTKL: mA = 0,6.44 + 0,7.18 - 0,95.32 = 8,6 (g)
=> 0,1.MX + 0,15.MY = 8,6
Do MY > 0 => MX < 86 (g/mol)
- Nếu X là CH4 => MY = \(\dfrac{140}{3}\) (Loại)
- Nếu X là C2H6 => MY = \(\dfrac{112}{3}\) (Loại)
- Nếu X là C3H8 => MY = 28 (C2H4)
- Nếu X là C4H10 => MY = \(\dfrac{56}{3}\) (Loại)
- Nếu X là C5H12 => MY = \(\dfrac{28}{3}\) (Loại)
Vậy X là C3H8, Y là C2H4

Giả sử trong 6,72 lít A có x mol C n H 2 n + 2 y mol C m H 2 m - 2 .
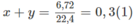
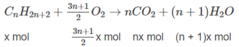
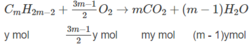
Số mol O 2 :
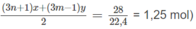
⇒(3n + 1)x + (3m − 1)y = 2,5 (2)
Số mol C O 2 : nx + my = 0,8 (mol)
⇒ (3n + 1)x + (3m - 1)y = 2,5 (3)
Từ (2) và (3) tìm được x - y = 0,1 ;
Kết hợp với X + y = 0,3, ta có: x = 0,2 và y = 0,1 Thay các giá trị tìm được vào (3) ta có
0,2n + 0,1m = 0,8
⇒ 2n + m = 8.
Nếu n = 1 thì m = 6: Loại, vì C 6 H 10 không phải là chất khí ở đktc. Nếu n = 2 thì m = 4. Công thức hai chất là C 2 H 6 và C 4 H 6 .
Nếu n = 3 thì m = 2: Loại vì m > 3.
Trả lời: Hỗn hợp A chứa (66,67%) và C 4 H 6 (33,33%)
Số mol H 2 O = (n + 1)x + (m - 1)y = 0,9 (mol).
2. Khối lượng nước: p = 0,9.18 = 16,2 (g).

Đáp án B
Ta có nCO2 = 0,3 mol ⇒ CTrung bình = 0 , 3 0 , 2 = 1,5.
⇒ Hỗn hợp ban đầu chứa CH4 và đồng đẳng của nó.
⇒ nH2O = nCO2 + nAnkan = 0,5 mol.
Mà mBình tăng = mCO2 + mH2O = 0,3×44 + 0,5×18 = 22,2 gam.

Đáp án C
Ta có mBình tăng = mCO2 + mH2O = 13,3 gam.
Với nCO2 = nBaCO3 = 0,2 mol ||⇒ nH2O = 0,25 mol.
Nhận thấy nC ÷ nH = 0,2 ÷ (0,25×2) = 2 ÷ 5

Bình 2 tăng 22 gam => mCO2 = 44 gam => nCO2 = 0,5 mol
C2H6 -> 2 CO2 + 3 H2O
C3H8 -> 3 CO2 + 4 H2O
Gọi nC2H6 = x mol, nC3H8 = y mol
x + y = 0,2 (1)
2x + 3y = 0,5 (2)
Nên: x = 0,1 mol, y = 0,1 mol
Vậy: % VC2H6 = 66,67 % => %VC3H8 = 33,33 %
mH2O = ( 3x + 4y ) . 18 = 12,6 gam

a) \(n_{BaCO_3}=\dfrac{49,25}{197}=0,25\left(mol\right)\)
Gọi a là số mol CO2 pư tạo thành Ba(HCO3)2
b là số mol H2O
PTHH: Ba(OH)2 + CO2 --> BaCO3 + H2O
0,25<-----0,25
Ba(OH)2 + 2CO2 --> Ba(HCO3)2
a
mdd giảm = 49,25 - 0,25.44 - 44a - 18b = 18,65
=> 44a + 18b = 19,6 (1)
Bảo toàn C: nC = a + 0,25 (mol)
Bảo toàn H: nH = 2b (mol)
=> 12(a + 0,25) + 2b = 6,6
=> 12a + 2b = 3,6 (2)
(1)(2) => a = 0,2; b = 0,6 (mol)
Vậy \(\left\{{}\begin{matrix}n_{CO_2\left(tổng\right)}=0,45\left(mol\right)\\n_{H_2O}=0,6\left(mol\right)\end{matrix}\right.\)
Bảo toàn O: \(n_{O_2}=\dfrac{0,45.2+0,6.1}{2}=0,75\left(mol\right)\)
=> V = 0,75.22,4 = 16,8 (l)
b) Xét nC ; nH = 0,45 : 1,2 = 3 : 8
=> CTPT: (C3H8)n (n thuộc N*)
Xét độ bất bão hòa \(\dfrac{2.3n+2-8n}{2}=1-n\)
=> n = 1
=> CTPT: C3H8
\(n_{BaCO_3}=n_C=n_{CO_2}=\dfrac{49,25}{197}=0,25\left(mol\right)\\ m_{ddgiam}=m_{\downarrow}-\left(m_{CO_2}+m_{H_2O}\right)\\ \Leftrightarrow18,65=49,25-\left(0,25.44+m_{H_2O}\right)\\ \Leftrightarrow m_{H_2O}=19,6\left(g\right)\\ \Rightarrow n_{H_2O}=\dfrac{49}{45}\left(mol\right)\\\Rightarrow n_H=\dfrac{98}{45}\left(mol\right)\\ m_C+m_H=0,25.12+\dfrac{98}{45}.1=5,178\left(g\right)\ne6,6\left(g\right)\)
Đề có sai ở đâu không em?

Dẫn sản phẩm cháy qua bình (I) đựng H2SO4 đặc thấy khối lượng bình (I) tăng 2,02 gam ⇒ mH2O = 2,02 ⇒ nH2O = 101/900
Dẫn sản phẩm cháy qua bình (II) đựng Ca(OH)2 thấy khối lượng bình (II) giảm 4,4 gam ⇒ mCaCO3 – mCO2 = 4,4. Ta có: nCO2 = nCaCO3
⇒ nCO2.(100 – 44) = 4,4 ⇒ nCO2 = 11/140
nH2O > nCO2 ⇒ 2 Hidrocacbon đó là ankan
Gọi công thức chung của 2 chất đó là CnH2n+2 (n>1)
Ta có: n CO2 : n H2O = n : (n+1) = 101/900 : 11/140 ⇒ n = 2,33
mà 2 ankan đồng đẳng kế tiếp ⇒ 2 chất đó là C2H6 và C3H8
Đáp án C.
1)
a) \(n_{CO_2}=\dfrac{26,4}{44}=0,6\left(mol\right)\)
\(n_{O_2}=\dfrac{21,28}{22,4}=0,95\left(mol\right)\)
Bảo toàn O: \(n_{H_2O}=0,95.2-0,6.2=0,7\left(mol\right)\)
=> Bình I tăng 0,7.18 = 12,6 (g)
b) \(n_{C_nH_{2n+2}}=0,7-0,6=0,1\left(mol\right)\)
=> \(n_{C_2H_4}=\dfrac{5,6}{22,4}-0,1=0,15\left(mol\right)\)
BTKL: \(m_X=0,6.44+0,7.18-0,95.32=8,6\left(g\right)\)
=> \(m_{C_nH_{2n+2}}=8,6-0,15.28=4,4\left(g\right)\)
=> \(M_{C_nH_{2n+2}}=\dfrac{4,4}{0,1}=44\left(g/mol\right)\)
=> n = 3
=> CTPT: C3H8
a) Gọi \(\left\{{}\begin{matrix}n_{CO_2}=a\left(mol\right)\\n_{H_2O}=b\left(mol\right)\end{matrix}\right.\)
\(n_{O_2}=\dfrac{17,36}{22,4}=0,775\left(mol\right)\)
Bảo toàn O: 2a + b = 1,55 (1)
\(n_{CaCO_3}=\dfrac{35}{100}=0,35\left(mol\right)\)
PTHH: Ca(OH)2 + CO2 --> CaCO3 + H2O
0,35<---0,35
Ca(OH)2 + 2CO2 --> Ca(HCO3)2
mdd giảm = 35 - 44a - 18b = 3,5
=> 44a + 18b = 31,5 (2)
(1)(2) => a = 0,45; b = 0,65
Bảo toàn C: nC = 0,45 (mol)
Bảo toàn H: nH = 1,3 (mol)
=> m = 0,45.12 + 1,3.1 = 6,7 (g)
b) Do \(n_{CO_2}< n_{H_2O}\) => 2 hidrocacbon là ankan
Gọi công thức chung của 2 ankan là \(C_{\overline{n}}H_{2\overline{n}+2}\)
=> \(n_{C_{\overline{n}}H_{2\overline{n}+2}}=0,65-0,45=0,2\left(mol\right)\)
=> \(M_{C_{\overline{n}}H_{2\overline{n}+2}}=\dfrac{6,7}{0,2}=33,5\left(g/mol\right)\)
Mà 2 ankan kế tiếp nhau
=> 2 ankan là C2H6 và C3H8
c) Gọi \(\left\{{}\begin{matrix}n_{C_2H_6}=x\left(mol\right)\\n_{C_3H_8}=y\left(mol\right)\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}2x+3y=0,45\\30x+44y=6,7\end{matrix}\right.\)
=> x = 0,15; y = 0,05
=> \(\left\{{}\begin{matrix}\%V_{C_2H_6}=\dfrac{0,15}{0,15+0,05}.100\%=75\%\\\%V_{C_3H_8}=\dfrac{0,05}{0,15+0,05}.100\%=25\%\end{matrix}\right.\)