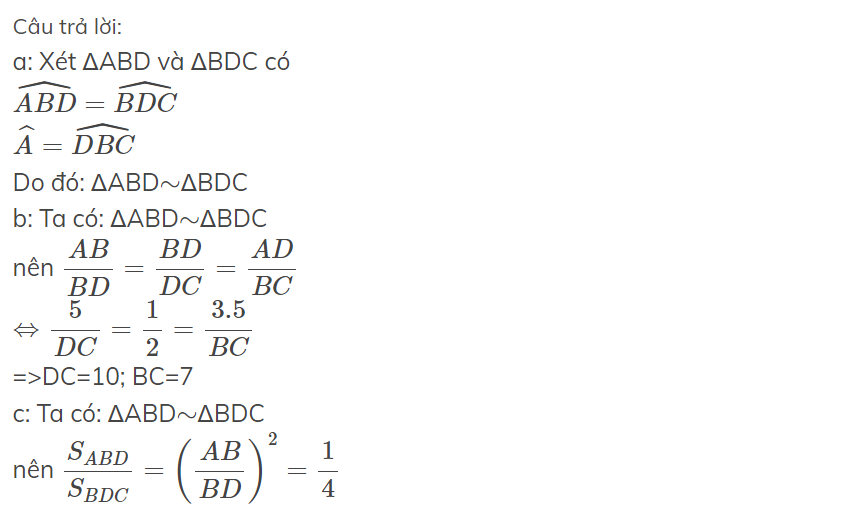Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: BC=căn 6^2+8^2=10cm
BD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=1
=>AD=3cm
b: Xét ΔABD vuông tại A và ΔEBC vuông tại E có
góc ABD=góc EBC
=>ΔABD đồng dạng với ΔEBC
c: ΔABD đồng dạng với ΔEBC
=>AD/EC=AB/EB
=>AD/AB=EC/EB
=>CD/BC=EC/EB

a: Xét ΔADB và ΔBCD có
\(\widehat{BAD}=\widehat{DBC}\)
\(\widehat{ABD}=\widehat{BDC}\)
Do đó: ΔADB\(\sim\)ΔBCD
b: Ta có: ΔADB\(\sim\)ΔBCD
nên DB/CD=AB/BD=AD/BC
=>5/CD=3/5=3,5/BC
=>CD=25/3(cm); BC=35/6(cm)

a) Dễ thấy : \(\Delta ABC\) đồng dạng với \(\Delta DEC\) (g.g) (Góc A = Góc CDE; góc C chung)
b) Từ a => \(\frac{AB}{DE}=\frac{AC}{DC}=\frac{BC}{EC}\)
c) Từ b => DC.BC = EC.AC

a: Xét ΔABD và ΔBDC có
\(\widehat{ABD}=\widehat{BDC}\)
\(\widehat{A}=\widehat{DBC}\)
Do đó: ΔABD\(\sim\)ΔBDC
b: Ta có: ΔABD\(\sim\)ΔBDC
nên \(\dfrac{AB}{BD}=\dfrac{BD}{DC}=\dfrac{AD}{BC}\)
\(\Leftrightarrow\dfrac{5}{DC}=\dfrac{1}{2}=\dfrac{3.5}{BC}\)
=>DC=10; BC=7
c: Ta có: ΔABD\(\sim\)ΔBDC
nên \(\dfrac{S_{ABD}}{S_{BDC}}=\left(\dfrac{AB}{BD}\right)^2=\dfrac{1}{4}\)