K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
10 tháng 10 2017
Đáp án B
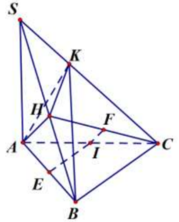
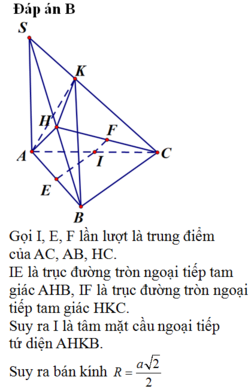
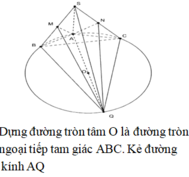
Gọi I, E, F lần lượt là trung điểm của AC, AB, HC. IE là trục đường tròn ngoại tiếp tam giác AHB, IF là trục đường tròn ngoại tiếp tam giác HKC.
⇒ IA=IB=IC=IH=IK
Suy ra I là tâm mặt cầu ngoại tiếp tứ diện AHKB.
Suy ra bán kính R= a 2 2

CM
24 tháng 10 2019
Đáp án B
Từ giả thiết ta có SO là trục của đường tròn ngoại tiếp tam giác ABC và SA=SB=a. Trong mặt phẳng (SAO), trung trực của cạnh SA cắt SO tại I thì I là tâm của mặt cầu ngoại tiếp hình chóp. Khi đó ta tính được:
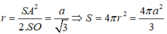

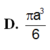
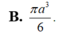
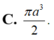
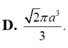


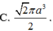
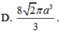
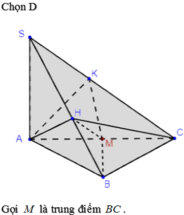

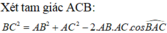



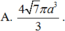
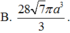
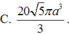
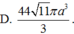







1.
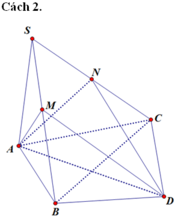
Gọi O là tâm đáy, M là trung điểm AB và N là trung điểm SB
\(SO=OM.tan\alpha=\frac{a.tan\alpha}{2}\)
Trong mặt phẳng (SBD), qua N kẻ trung trực SB cắt SO tại I
\(\Rightarrow\) I là tâm mặt cầu ngoại tiếp chóp
\(SB^2=\sqrt{OB^2+SO^2}=\frac{2a^2+a^2.tan^2\alpha}{4}\)
Hai tam giác vuông BOS và INS đồng dạng \(\Rightarrow\frac{SI}{SB}=\frac{SN}{SO}\Rightarrow R=SI=\frac{SB.SN}{SO}=\frac{SB^2}{2SO}=\frac{2a+a.tan^2\alpha}{4tan\alpha}\)
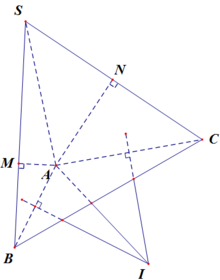
2.
Gọi M và N lần lượt là trung điểm AB, AC \(\Rightarrow\) M và N lần lượt là tâm đường tròn ngoại tiếp các tam giác vuông ABH và ACK
Trong mặt phẳng (ABC), qua M và N lần lượt kẻ trung trực của AB và AC, chúng cắt nhau tại I
\(\Rightarrow\left\{{}\begin{matrix}IN\perp\left(ACK\right)\\IM\perp\left(ABH\right)\end{matrix}\right.\) \(\Rightarrow IA=IB=IC=IH=IK\)
Hay I là tâm đường tròn ngoại tiếp đa diện A,B,C,H,K
Hay 5 điểm A,B,C,H,K cùng thuộc 1 mặt cầu
b. Bán kính mặt cầu đã cho bằng bán kính đường tròn ngoại tiếp tam giác ABC
\(BC=\sqrt{AB^2+AC^2-2AB.AC.cos60^0}=\sqrt{7}\)
\(\Rightarrow R=\frac{AB.BC.CA}{4S_{ABC}}=\frac{AB.BC.CA}{4.\frac{1}{2}.AB.AC.sin60^0}=\frac{\sqrt{21}}{3}\)