Question

[BÁ Long]

1)cho hình chóp S.ABCD có đáy là hình thoi cạnh a góc BAD = 60 độ cạnh bên SA = a và SA vuông góc với mặt đáy. Tính khoảng cách từ B đến mặt phẳng SCD ?

2)cho hình chóp S.ABCD có ABCD là hình thoi cạnh a , góc ABC = 60 độ , SA vuông góc với đáy , SA = \(\frac{3a}{2}\). gọi O là tâm hình thoi. khoảng cách từ O đến mặt phẳng SBC bằng ?

Answer 1

[Nguyễn Việt Lâm]

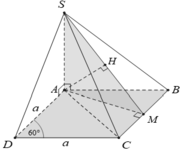
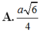
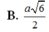
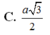
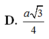
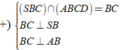
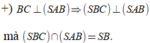
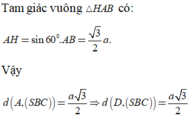
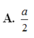
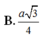
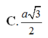
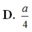
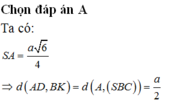
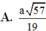
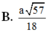
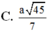
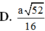
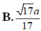
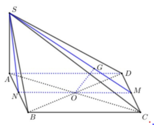
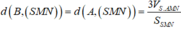
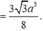
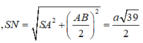
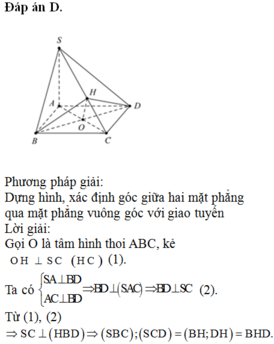
Làm biếng vẽ hình quá, bạn tự vẽ :D

1/ Dễ dàng nhận ra các tam giác BAD và BCD đều

Do \(AB//\left(SCD\right)\Rightarrow d\left(B;\left(SCD\right)\right)=d\left(A;\left(SCD\right)\right)\)

Từ A kẻ \(AH\perp CD\Rightarrow AH=\frac{a\sqrt{3}}{2}\Rightarrow CD\perp\left(SAH\right)\)

Từ A kẻ \(AK\perp SH\Rightarrow AK\perp\left(SCD\right)\)

\(\Rightarrow AK=d\left(A;\left(SCD\right)\right)=d\left(B;\left(SCD\right)\right)\)

Áp dụng hệ thức lượng: \(\frac{1}{AK^2}=\frac{1}{AH^2}+\frac{1}{SA^2}\Rightarrow AK=\frac{SA.AH}{\sqrt{SA^2+AH^2}}=...\)

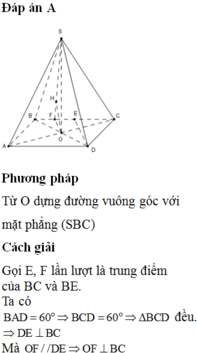
Câu 2:

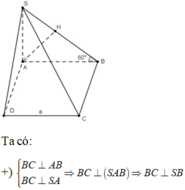
OA cắt \(\left(SBC\right)\) tại C, mà O là trung điểm AC

\(\Rightarrow d\left(O;\left(SBC\right)\right)=\frac{1}{2}d\left(A;\left(SBC\right)\right)\)

Tương tự như câu trên, tam giác ABC đều, từ A kẻ \(AH\perp BC\Rightarrow BC\perp\left(SAH\right)\)

\(\Rightarrow AH=\frac{a\sqrt{3}}{2}\)

Từ A kẻ \(AK\perp SH\Rightarrow AK\perp\left(SBC\right)\)

\(\Rightarrow AK=d\left(A;\left(SBC\right)\right)=2d\left(O;\left(SBC\right)\right)\)

Áp dụng hệ thức lượng:

\(\frac{1}{AK^2}=\frac{1}{AH^2}+\frac{1}{SA^2}\Rightarrow d\left(O;\left(SBC\right)\right)=\frac{1}{2}AK=\frac{SA.AH}{2\sqrt{SA^2+AH^2}}=...\)