Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
.png)
0). Vẽ AH ^ BC tại H
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
Suy ra: \(\widehat{BAH}=\widehat{CAH}\)
hay AH là tia phân giác của góc BAC
b: Xét ΔEAH vuông tại E và ΔFAH vuông tại F có
AH chung
\(\widehat{EAH}=\widehat{FAH}\)
Do đó: ΔEAH=ΔFAH
Suy ra: HE=HF
hay ΔHEF cân tại H
c: Xét ΔACK và ΔABK có
AC=AB
\(\widehat{CAK}=\widehat{BAK}\)
AK chung
Do đó: ΔACK=ΔABK
Suy ra: \(\widehat{ACK}=\widehat{ABK}=90^0\)
=>BK\(\perp\)AB
hay BK//EH
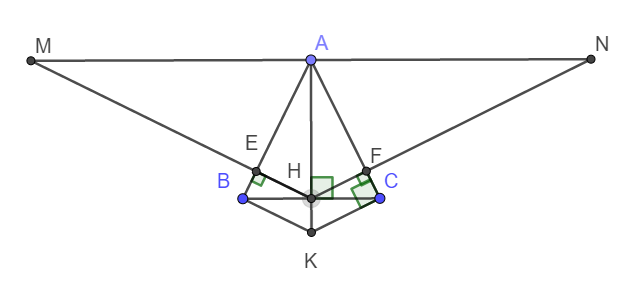
a) Xét tam giác vuông ABH và tam giác vuông ACH có:
Cạnh AH chung
AB = AC (gt)
\(\Rightarrow\widehat{BAH}=\widehat{CAH}\) (Hai góc tương ứng)
Vậy nên AH là tia phân giác góc BAC.
b) Xét hai tam giác vuông AEH và AFH có:
Cạnh AH chung
\(\widehat{EAH}=\widehat{FAH}\)
\(\Rightarrow\Delta AEH=\Delta AFH\) (Cạnh huyền - góc nhọn)
\(\Rightarrow HE=HF\) (Hai cạnh tương ứng)
Suy ra tam giác HEF cân tại E.
c) Dễ thấy \(\Delta ABK=\Delta ACK\left(c-g-c\right)\)
\(\Rightarrow\widehat{AKB}=\widehat{AKC}\)
Lại có \(\widehat{AKC}=\widehat{AHF}\) (Đồng vị)
\(\widehat{AHF}=\widehat{AHE}\) (Do \(\Delta AEH=\Delta AFH\) )
\(\Rightarrow\widehat{AKB}=\widehat{AHE}\) hay HE // BK
d) Ta có \(\Delta AHN=\Delta AHM\left(c-g-c\right)\)
\(\Rightarrow\widehat{MAH}=\widehat{NAH}=90^o\)
\(\Rightarrow\widehat{MAN}=180^o\) hay M, N, A thẳng hàng.
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
DO đó: ΔAHB=ΔAHC
Suy ra: \(\widehat{BAH}=\widehat{CAH}\)
hay AH là tia phân giác
b: Xét ΔEAH vuông tại E và ΔFAH vuông tại F có
AH chung
\(\widehat{EAH}=\widehat{FAH}\)
Do đó: ΔEAH=ΔFAH
Suy ra: HE=HF
hay ΔHEF cân tại H