
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\sqrt{\left(\sqrt{2}-1\right)^2}-\sqrt{11+6\sqrt{2}}\)
\(=\sqrt{2}-1-3-\sqrt{2}\)
=-4
b) \(\sqrt{\left(1-\sqrt{5}\right)^2}+\sqrt{14-6\sqrt{5}}\)
\(=\sqrt{5}-1+3-\sqrt{5}\)
=2
c) \(\sqrt{21-12\sqrt{3}}-\sqrt{13-4\sqrt{3}}\)
\(=2\sqrt{3}-3-2\sqrt{3}+1\)
=-2

a) \(17-12\sqrt{2}=\left(3-2\sqrt{2}\right)^2\)
b) \(57-24\sqrt{3}=\left(4\sqrt{3}-3\right)^2\)
c) \(x+2\sqrt{2x-4}=\left(\sqrt{x-2}+\sqrt{2}\right)^2\)

\(\sqrt{21-12\sqrt{3}}=\sqrt{21-2.\sqrt{36}.\sqrt{3}}=\sqrt{21-2\sqrt{108}}=\sqrt{12-2.\sqrt{12}.\sqrt{9}+9}=\sqrt{\left(\sqrt{12}-3\right)^2}=\sqrt{12}-3\)

a, \(2\sqrt{3}-\sqrt{4+x^2}=0\Leftrightarrow\sqrt{4+x^2}=2\sqrt{3}\)
\(\Leftrightarrow x^2+4=12\Leftrightarrow x^2=8\Leftrightarrow x=\pm2\sqrt{2}\)
b, \(\sqrt{16x+16}-\sqrt{9x+9}=0\)ĐK : x >= -1
\(\Leftrightarrow4\sqrt{x+1}-3\sqrt{x+1}=0\Leftrightarrow\sqrt{x+1}=0\Leftrightarrow x+1=0\Leftrightarrow x=-1\)
c, \(\sqrt{4\left(x+2\right)^2}=8\Leftrightarrow2\left|x+2\right|=8\Leftrightarrow\left|x+2\right|=4\)
TH1 : \(x+2=4\Leftrightarrow x=2\)
TH2 : \(x+2=-4\Leftrightarrow x=-6\)
c: Ta có: \(\sqrt{4\left(x+2\right)^2}=8\)
\(\Leftrightarrow\left|x+2\right|=4\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=4\\x+2=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-6\end{matrix}\right.\)

sin 650=cos 350
\(cos70^0=sin30^0\)
\(tan80^0=cot20^0\)
\(cot68^0=tan32^0\)

4x^2 - 7x -2 = 4x^2 - 8x + x - 2 = 4x(x - 2) + (x - 2) = (x -2)(4x + 1)

Ta có: (căn x+y)2=(căn x+z + căn y+x)2
suy ra:x+y=(căn x+z)2 +2(căn x+z)(căn y+z)+(căn y+z)2
suy ra:x+y=x+z+y+z+2[căn (x+z)(y+z)]
suy ra:-z=căn (x+z)(y+z)
suy ra:(-z)2=[căn (x+z)(y+z)]2
suy ra:z2=(x+z)(y+z)
suy ra:z2=xy+xz+yz+z2
suy ra:xy+yz+xz=0
suy ra:(xy+yz+xz)/xyz=0(vì x,y,z khác 0)
suy ra:xy/xyz+yz/xyz+xz/xyz=0
suy ra:1/x+1/y+1/z=0(ĐPCM)
K CHO MÌNH VỚI NHA

\(\sqrt{a}+\sqrt{b}\ge\sqrt{a+b}\)
Bình 2 vế của pt do 2 vế dương ta có:
\(\left(\sqrt{a}+\sqrt{b}\right)^2\ge\left(\sqrt{a+b}\right)^2\)
\(\Leftrightarrow a+b+2\sqrt{ab}\ge a+b\)
\(\Leftrightarrow2\sqrt{ab}\ge0\Leftrightarrow\sqrt{ab}\ge0\) (luôn đúng)
Tức ta có điều phải cm
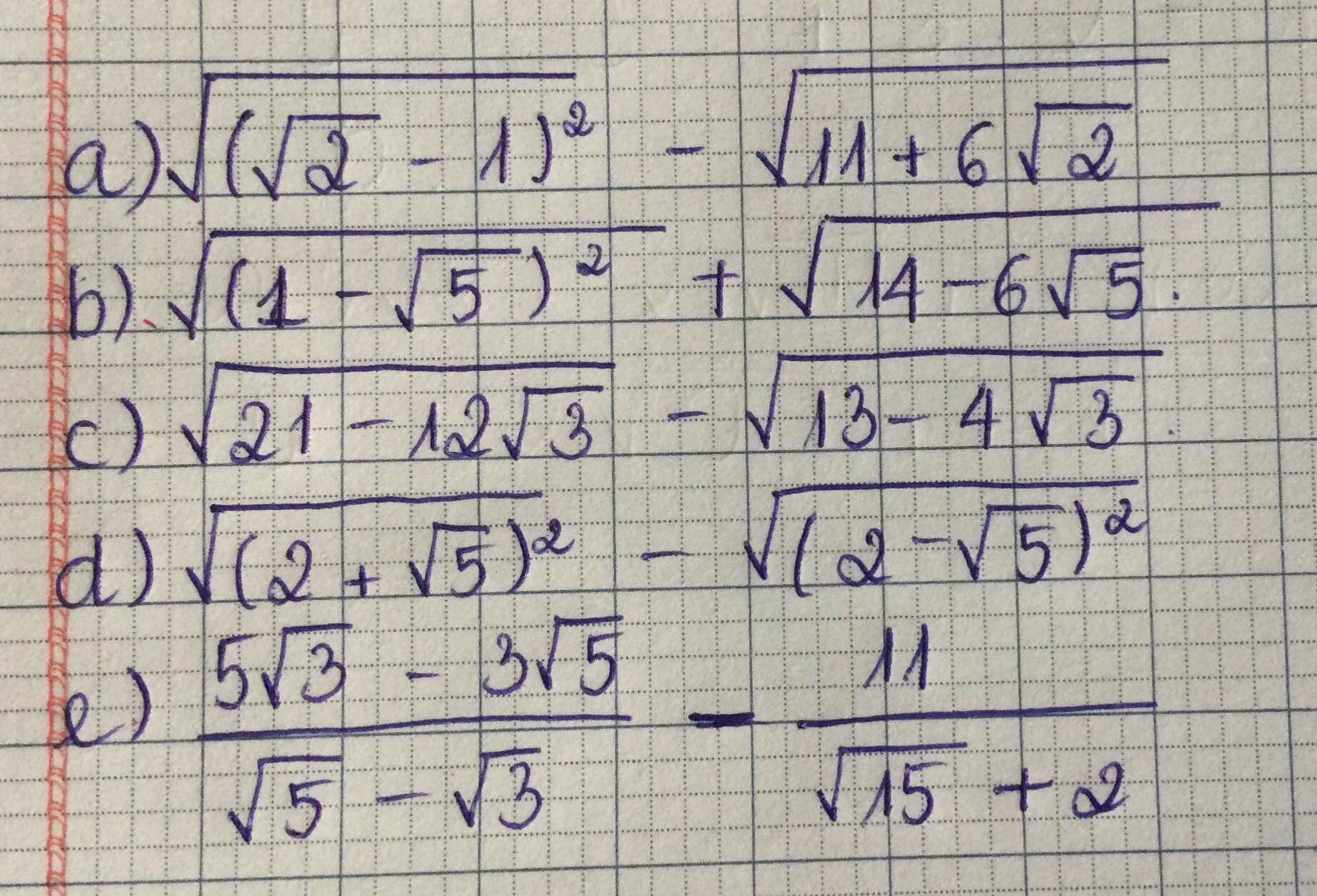 Tính và thu gọn biểu thức.
Tính và thu gọn biểu thức.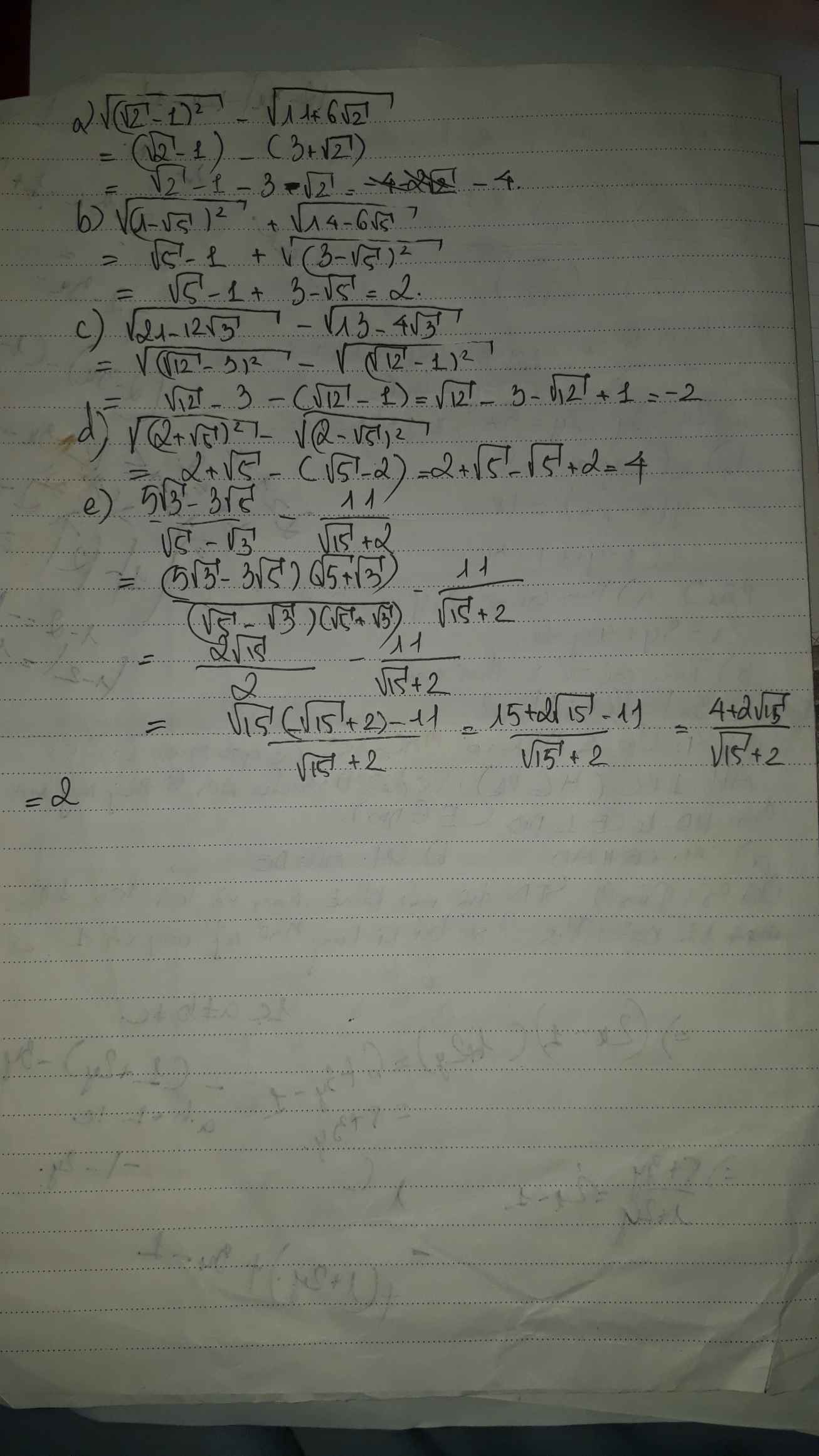
 Các bạn ơi giúp mk với. Mk cần gấp lắm ạ.Các bạn giải chi tiết giúp mk nhé . Mk hứa sẽ vote 5* cho . Mk cảm ơn nhiều.
Các bạn ơi giúp mk với. Mk cần gấp lắm ạ.Các bạn giải chi tiết giúp mk nhé . Mk hứa sẽ vote 5* cho . Mk cảm ơn nhiều.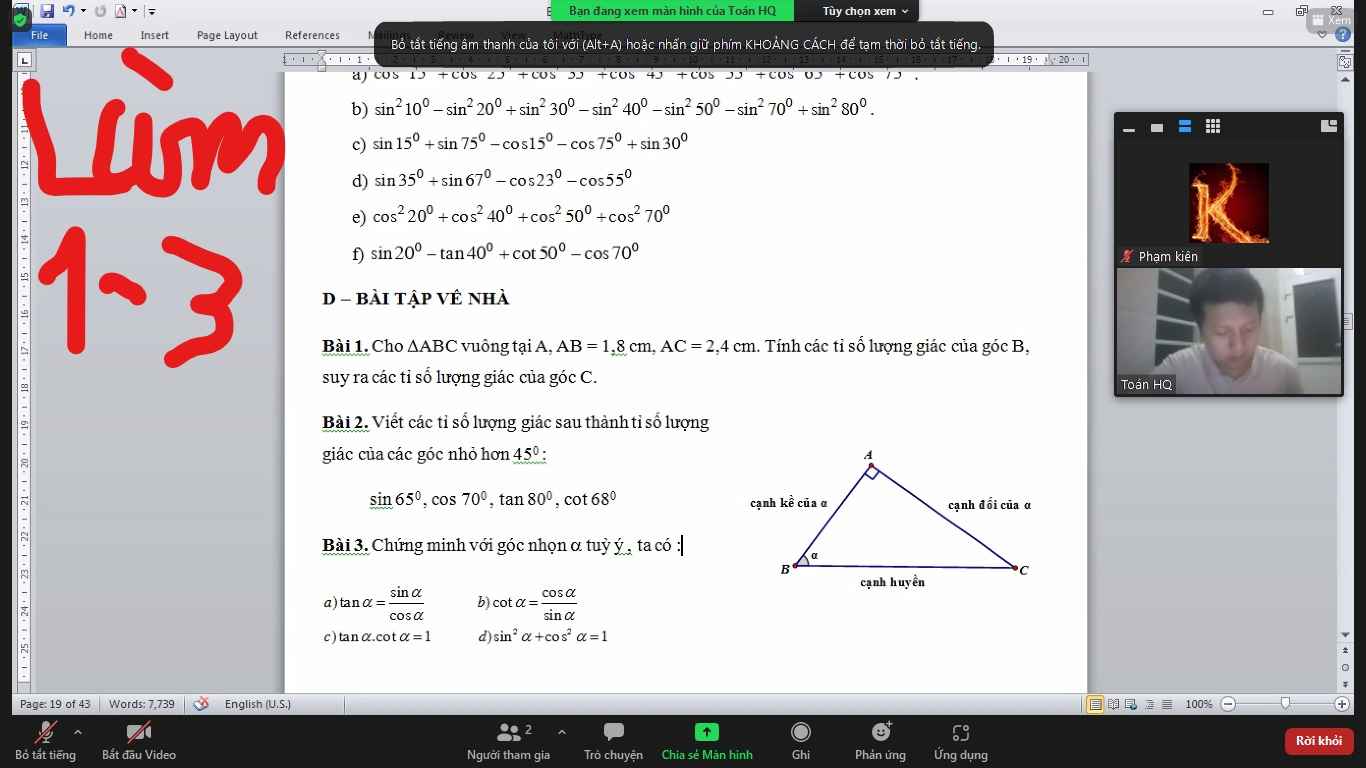
`\sqrt{17-12\sqrt{2}}`
`=\sqrt{17-6.\sqrt{4}.\sqrt{2}}`
`=\sqrt{17-6\sqrt{8}}`
`=\sqrt{9-2.3.\sqrt{8}+8}`
`=\sqrt{(3-\sqrt{8})^{2}}`
`=|3-\sqrt{8}|`
`=3-\sqrt{8}` ( Vì `3=\sqrt{9}>\sqrt{8}` )