

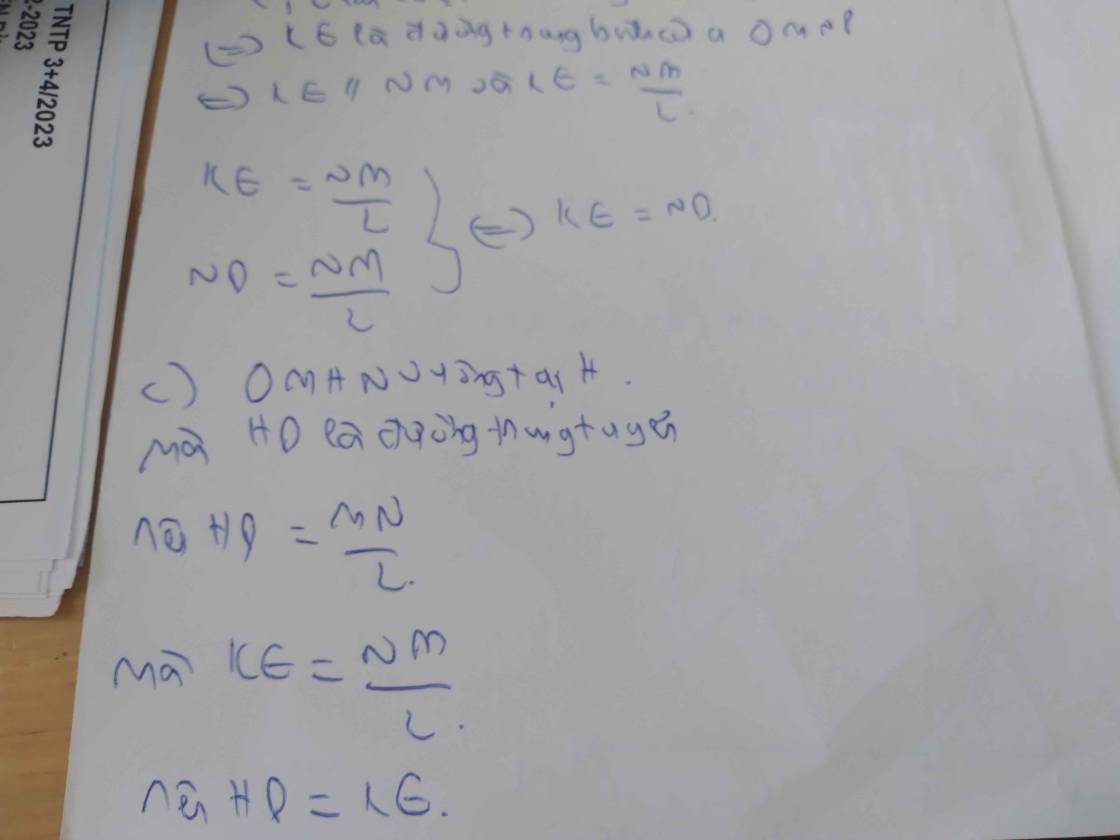

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



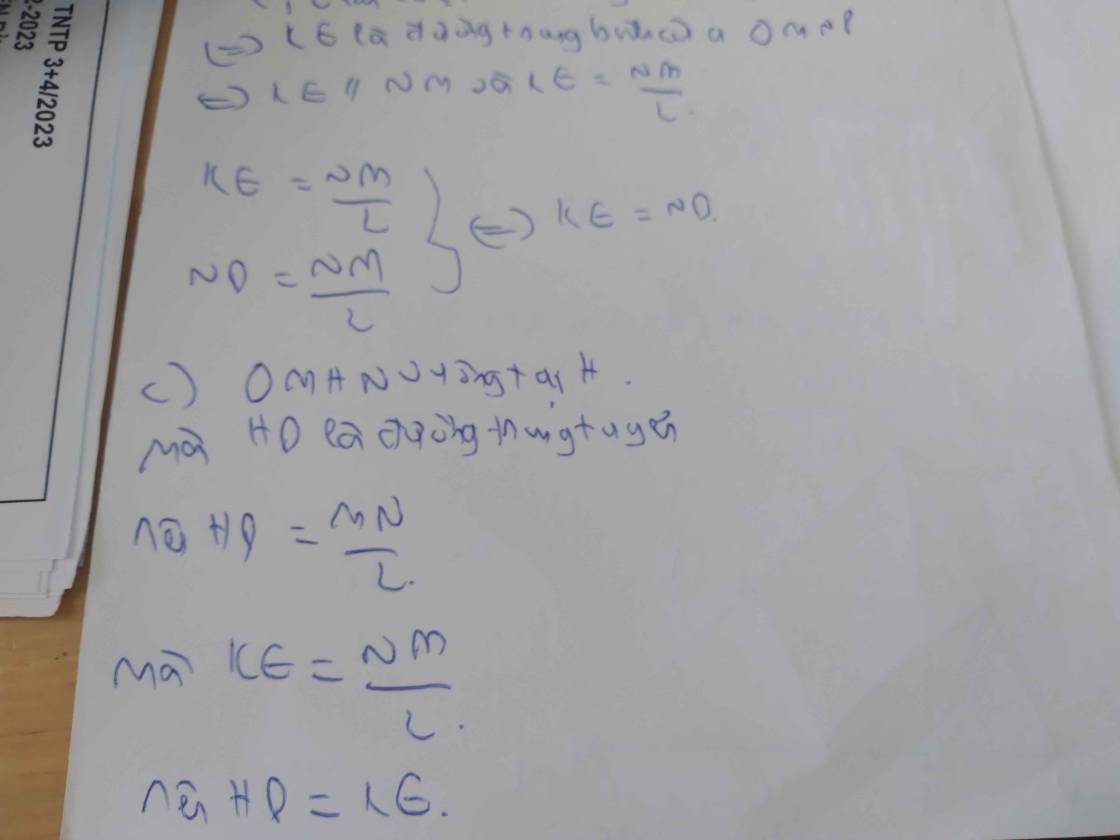


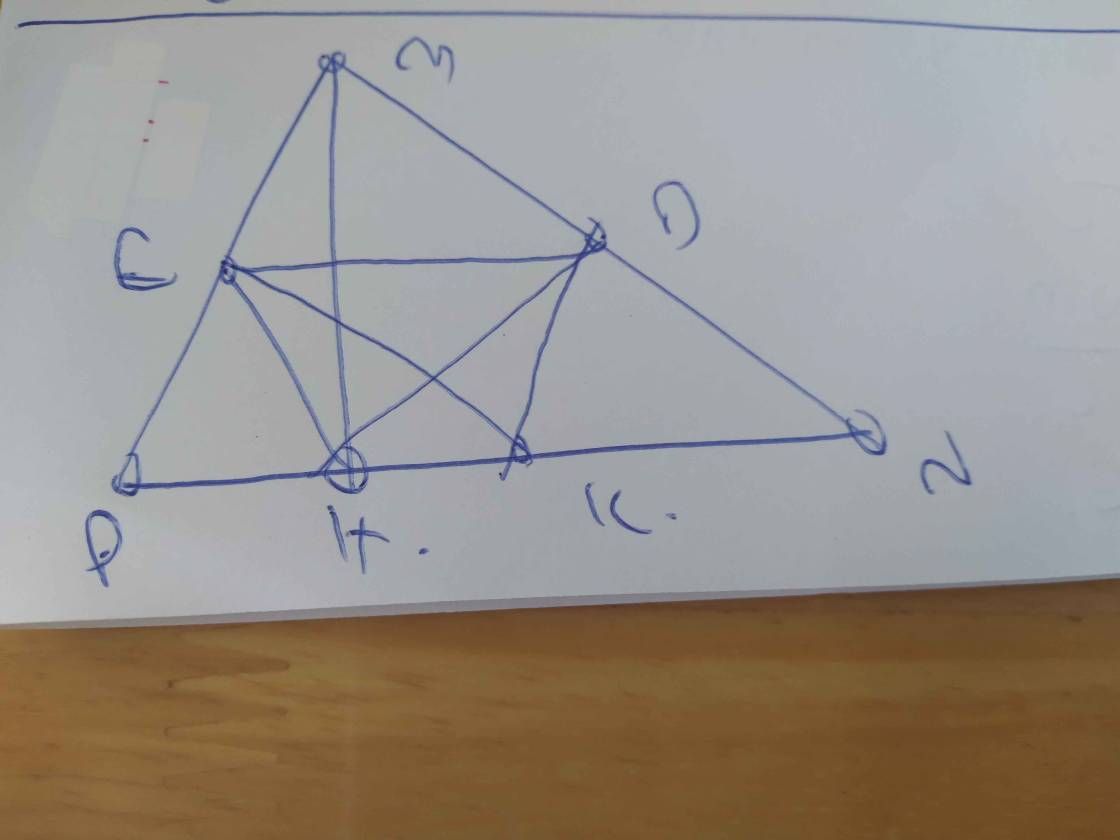
a: Xét tứ giác MDHE có
\(\widehat{MDH}=\widehat{MEH}=\widehat{EMD}=90^0\)
=>MDHE là hình chữ nhật
b: MDHE là hình chữ nhật
=>MH cắt DE tại trung điểm của mỗi đường
mà O là trung điểm của MH
nên O là trung điểm của DE
=>DO=OE
c: ΔHDN vuông tại D
mà DI là đường trung tuyến
nên DI=HI=IN
=>ΔIHD cân tại I
ΔPEH vuông tại E
mà EK là đường trung tuyến
nên EK=KP=KH
=>ΔKEH cân tại K
\(\widehat{KED}=\widehat{KEH}+\widehat{DEH}\)
\(=\widehat{KHE}+\widehat{HMD}\)
\(=\widehat{HMD}+\widehat{HND}=90^0\)
=>KE vuông góc ED(1)
\(\widehat{IDE}=\widehat{IDH}+\widehat{EDH}\)
\(=\widehat{IHD}+\widehat{EMH}\)
\(=\widehat{HPM}+\widehat{HMP}=90^0\)
=>ID vuông góc DE(2)
Từ (1) và (2) suy ra DI//EK

a: Xét ΔMNQ có
A là trung điểm của MN
D là trung điểm của MQ
Do đó: AD là đường trung bình của ΔMNQ
Suy ra: AD//QN và AD=QN/2(1)
Xét ΔNPQ có
B là trung điểm của NP
C là trung điểm của QP
Do đó: BC là đường trung bình của ΔNPQ
Suy ra: BC//NQ và BC=NQ/2(2)
Từ (1) và (2) suy ra AD//BC và AD=BC
hay ABCD là hình bình hành
Cho hình thang cân MNPQ( MN//PQ). Gọi A, B, C , D lần lượt là trung điểm của MN, NP, PQ, MQ. Tứgiác ABCD là hình gì? ( Giúp mình với, mìn cảm ơn các b nhìu lắm lun, làm ơn giúp mình đi mà))
*Gợi ý: +MP = NQ theo tính chất hìnhthang cân
+ Sửdụng tính chất đường trung bình của tam giác Chứng minh tứgiác ABCD là hình thoi theo dấu hiệu tứgiác có bốn cạnh bằng nhau

a: Xét ΔHNM vuông tại H và ΔMNP vuôg tại M có
góc N chung
=>ΔHNM đồng dạng với ΔMNP
b: NP=căn 3^2+4^2=5cm
MH=3*4/5=2,4cm
NH=3^2/5=1,8cm
c; Đề bài yêu cầu gì?

a: Xét ΔMNP có
D là trung điểm của MP
E là trung điểm của MN
Do đó: DE là đường trung bình của ΔMNP
Suy ra: DE//NP
hay PDEN là hình thang vuông
DE=NP/2=11(cm)

a: Xét tứgiác MIHK có
góc MIH=góc MKH=góc KMI=90 độ
nên MIHKlà hình chữ nhật
=>MH=IK
b: Xét ΔNMP có
H là trung điểm của NP
HI//MP
Do dó: Ilàtrung điểm của MN
Xet ΔNMP có
H là trung điểm của PN
HK//MN
Do đó;K là trung điểm của MP
Xét ΔMHN có NI/NM=ND/NH
nên DI//MH và DI=MH/2
Xét ΔPMH có PK/PM=PE/PH
nên KE//MH và KE=MH/2
=>DI//KE và DI=KE
=>DIKE là hình bình hành