Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Xét tứ giác BEDC có \(\widehat{BEC}=\widehat{BDC}=90^0\)
nên BEDC là tứ giác nội tiếp
2: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc BAD chung
Do đó:ΔADB\(\sim\)ΔAEC
Suy ra: AD/AE=AB/AC
hay AD/AB=AE/AC
Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
Do đó: ΔADE\(\sim\)ΔABC
hay \(\widehat{ADE}=\widehat{ABC}\)

a: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
b:
Xét ΔMEB và ΔMCF có
góc MEB=góc MCF
góc M chung
=>ΔMEB đồg dạg vơi ΔMCF
=>ME/MC=MB/MF
=>ME/MB=MC/MF
Xét ΔAMF và ΔEMK có
MA/ME=MF/MK
góc AMF=góc EMK
=>ΔAMF đồng dạng với ΔEMK
=>góc FAM=góc KEM
=>AEFK nội tiếp
mà AEHK nội tiếp
nên A,E,F,K,H cùng thuộc 1 đường tròn

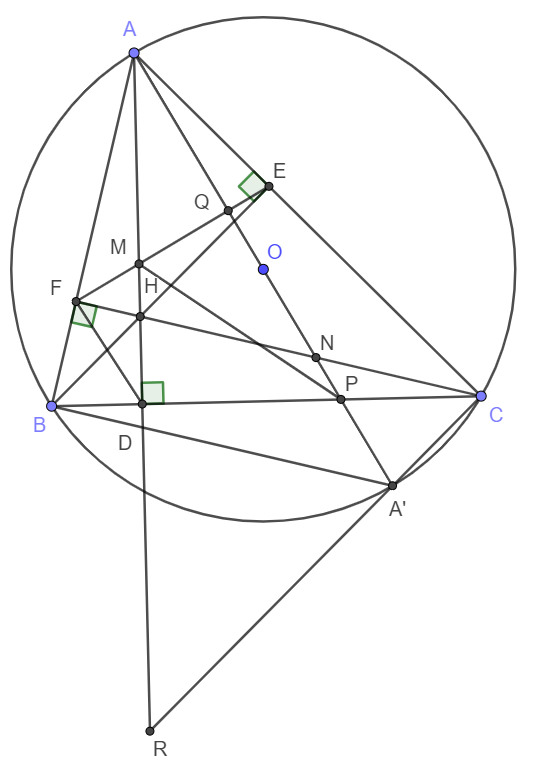
a) theo gt, BFC=BEC=90
=> BFEC nội tiếp (có 2 góc kề bang nhau)
góc AFC=ADC=90 => AFDC nội tiếp ( có 2 cạnh kề cùng nhìn một đoan thẳng bằng nhau)
b) vì tứ giác ABA'C nội tiếp => ABC = AA'C (cùng chắn cung AC)
Lại có ABC= AHF (Cùng phụ với góc BAD)
Ta thấy AFHE nội tiếp vì AFH +AEH = 90+90=180
=> AHF=AEF (Cùng chắn cung AF)
=>Đpcm
c) vì tứ giác EQA'C nôi tiếp
nên EQA'+ECA'=180 mà ECA'=90 vì là góc nội tiếp chắn nửa đường tròn
=> MQP=EQA'=90 ( vì MQP+EQA=180)
Trong đó ADC=90 =>Đpcm
d) Vì ABA'C VÀ FBDH nội tiếp nên góc NA'C=ABC=DHC
=>NA'C=DHC=>Đpcm

a:
H đối xứng K qua BC
=>BH=BK CH=CK
Xét ΔBHC và ΔBKC có
BH=BK
HC=KC
BC chung
=>ΔBHC=ΔBKC
=>góc BHC=góc BKC
góc BHC=180 độ-góc HBC-góc HCB
=90 độ-góc HBC+90 độ-góc HCB
=góc ABC+góc ACB
=180 độ-góc BAC
=>góc BAC+góc BHC=180 độ
=>góc BAC+góc BKC=180 độ
=>ABKC là tứ giác nội tiếp
b: Xét (O) có
ΔABM nội tiếp
AM là đường kính
=>ΔABM vuông tại B
=>BM//CH
Xét (O) có
ΔACM nội tiếp
AM là đường kinh
=>ΔACM vuông tại C
=>CM//BH
mà BM//CH
nên BHCM là hình bình hành
=>CB căt HM tại trung điểm của mỗi đường
=>H,I,M thẳng hàng
