K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HN
6 tháng 3 2017
\(|\frac{a-b}{a+b}+\frac{b-c}{b+c}+\frac{c-a}{c+a}|=|\frac{\left(a-b\right)\left(c-a\right)\left(c-b\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}|\)
Không mất tính tổng quát ta giả sử \(a\ge b\ge c\)
\(\Rightarrow|\frac{\left(a-b\right)\left(c-a\right)\left(c-b\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}|=\frac{a-b}{a+b}.\frac{a-c}{a+c}.\frac{b-c}{b+c}< 1\)
Vì \(\left\{\begin{matrix}a-b< a+b\\b-c< b+c\\a-c< a+c\end{matrix}\right.\)
Vậy ta có ĐPCM
9 tháng 3 2023
Bài 2:
a: VTPT là (-1;4)
PTTQ là:
-1(x+3)+4(y-2)=0
=>-x-3+4y-8=0
=>-x+4y-11=0
=>x-4y+11=0
b: Phương trình tổng quát là:
3(x+5)+2(y-2)=0
=>3x+15+2y-4=0
=>3x+2y+11=0
c: vecto CD=(4;3)
=>VTPT là (-3;4)
PTTQ là:
-3(x-5)+4(y-3)=0
=>-3x+15+4y-12=0
=>-3x+4y+3=0
MT
2
NT
28 tháng 7 2016
quy đồng lên thì dc
(ax^2-a^2a+b^2*x-b^2*c)=x^2-cx-dx+cd
<=>x^2(a-1)+x(b^2+c+d)-(a^2*d+b^2c+cd)=0
đen ta =(a-1)^2+4(b^2+c+d)(a^2a+b^2c+cd)
giải ra đen ta >0 là dc
16 tháng 5 2022
bài này hình như sai đề ấy nhỉ, thử thay x=0 vào thì bt thỏa mãn khi a≥1, vậy thì làm gì có đáp án nhỉ :3
17 tháng 5 2022
(1- a)( x +x -1)\(\ge\) 0
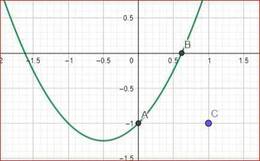
xem hình vẽ parabol (x + x - 1) , trong khoảng [0,1] thì luôn âm, muốn bất đẳng thức dương thì ( 1 - a) phải âm.
1 - a ≤ 0
1 ≤ a ≤ + ∞
a nhỏ nhất là 1. còn lớn nhất là số dương không xác định.
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 3 2022
\(\Leftrightarrow\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}+3\ge\dfrac{2\left(a+b+c\right)}{abc}=2\left(\dfrac{1}{ab}+\dfrac{1}{ac}+\dfrac{1}{bc}\right)\)
Đặt \(\left(\dfrac{1}{a};\dfrac{1}{b};\dfrac{1}{c}\right)=\left(x;y;z\right)\Rightarrow xyz=1\)
BĐT trở thành: \(x^2+y^2+z^2+3\ge2\left(xy+yz+zx\right)\)
Theo nguyên lý Dirichlet, trong 3 số x;y;z luôn có ít nhất 2 số cùng phía so với 1
Không mất tính tổng quát, giả sử đó là x và y \(\Rightarrow\left(x-1\right)\left(y-1\right)\ge0\)
\(\Rightarrow xy+1\ge x+y\Rightarrow xyz+z\ge xz+yz\Rightarrow2xyz+2z\ge2xz+2yz\)
\(\Rightarrow2\ge2xz+2yz-2z\) (do \(xyz=1\))
\(\Rightarrow VP=x^2+y^2+z^2+2+1\ge x^2+y^2+z^2+2xz+2yz-2z+1\)
\(VP\ge2xy+z^2+2xz+2yz-2z+1=2\left(xy+yz+zx\right)+\left(z-1\right)^2\ge2\left(xy+yz+zx\right)\) (đpcm)
Dấu "=" xảy ra khi \(x=y=z=1\) hay \(a=b=c=1\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 10 2019
Đề bài sai, tập B không hề tồn tại do \(b+1>b\) với mọi b
Ví dụ như các tập \(\left[3;2\right]\) không tồn tại, chỉ có \(\left[2;3\right]\) thôi