Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(2,f\left(0\right)=0+1=1;f\left(-1\right)=-3+1=-2\\ 3,\\ a,\left\{{}\begin{matrix}AB=AC\\BM=MC\\AM\text{ chung}\end{matrix}\right.\Rightarrow\Delta ABM=\Delta ACM\left(c.c.c\right)\\ b,\Delta ABM=\Delta ACM\\ \Rightarrow\widehat{B}=\widehat{C}\\ c,\left\{{}\begin{matrix}AB=AC\\AM=MD\\\widehat{AMB}=\widehat{CMD}\left(đđ\right)\end{matrix}\right.\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\\ \Rightarrow\widehat{B}=\widehat{MCD}\\ \text{Mà 2 góc này ở vị trí so le trong nên }AB\text{//}CD\)

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM

a: Xét ΔABM và ΔACM có
AM chung
AB=AC
BM=CM
Do đó: ΔABM=ΔACM
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét tứ giác ABDC có
M là trung điểm của BC
M la trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB//CD

b) Vì AB=AC
⇒ ∆ABC cân tại A
⇒ AM là đường trung tuyến đồng thời là đường cao, phân giác
⇒ AM⊥BC
a) Xét ∆ABM và ∆ACM có:
AM: cạnh chung
^M1=^M2=90o(Vì AM⊥BC)
MB=MC(gt)
⇒ ∆ABM=∆ACM (c.g.c)
c) Xét ∆AMB và ∆DMC có:
MA=MD(gt)
^M1=^M3(đối đỉnh)
MB=MC(gt)
⇒ ∆AMB=∆DMC (c.g.c)
⇒ ^A1=^D1(t/ứ)
mà 2 góc có vị trí so le trong
⇒ CD//AB

Bài 3:
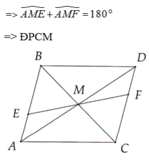
a: Xét ΔAEM và ΔCEB có
EA=EC
\(\widehat{AEM}=\widehat{CEB}\)
EM=EB
Do đó: ΔAEM=ΔCEB
b: Xét tứ giác ABCM có
E là trung điểm của AC
E là trung điểm của BM
Do đó: ABCM là hình bình hành
Suy ra: AM//BC
a: Xét ΔAEM và ΔCEB có
EA=EC
ˆAEM=ˆCEB
EM=EB
Do đó: ΔAEM=ΔCEB
b: Xét tứ giác ABCM có
E là trung điểm của AC
E là trung điểm của BM
Do đó: ABCM là hình bình hành
Suy ra: AM//BC