Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bạn ơi, xem lại đề ra 1 chút, hình như có câu sai đề thì phải


Điều kiện: x ≠ 1 ; x ≠ - 3
Ta có
10 - 3 3 - x x - 1 > 10 + 3 x + 1 x + 3 ⇔ 10 + 3 x - 3 x - 1 > 10 + 3 x + 1 x + 3 ⇔ x - 3 x - 1 > x + 1 x + 3 ⇔ - 8 x - 1 x + 3 > 0 ⇔ x - 1 x + 3 < 0 ⇔ - 3 < x < 1
Do x ∈ Z nên x ∈ - 2 ; - 1 ; 0 .
Vậy bất phương trình đã cho có 3 nghiệm nguyên.
Đáp án D

Đáp án D
P T ⇔ π 4 3 x − 9 x 2 − 16 x − 80 = k π ⇔ 3 x − 9 x 2 − 16 x − 80 = 4 k ⇔ 9 x 2 − 16 x − 80 = 3 x − 4 k ⇔ 3 x ≥ 4 k 9 x 2 − 16 x − 80 = 9 x 2 − 24 k x + 16 k 2
Xét 9 x = 18 k 2 + 90 3 k − 2 = 2 9 k 2 − 4 + 98 3 k − 2 = 2 3 k + 2 + 98 3 k − 2
D o x ∈ ℕ * ⇒ 3 k − 2 = 1 ; 2 ; 7 ; 14 ; 49 ; 98 → k ∈ ℤ k = 1 ⇒ x = 12 k = 3 ⇒ x = 4 k = 17 ⇒ x = 12
Chỉ có 2 nghiệm k ; x = 1 ; 12 ; 3 ; 4 thỏa mãn 3 x ≥ 4 k

Điều kiện 9 x 2 - 16 x - 80 ≥ 0 ⇔ x ≥ 4
Phương trình đã cho tương đương với
π 4 3 x - 9 x 2 - 16 x - 80 = k π k ∈ ℤ ⇔ 3 x - 9 x 2 - 16 x - 80 = 4 k ⇔ 9 x 2 - 16 x - 80 = 3 x - 4 k ⇔ x ≥ 4 k 3 9 x 2 - 16 x - 80 = 3 x - 4 k 2 ⇔ x ≥ 4 k 3 x = 2 k 2 + 10 3 k - 2
Yêu cầu bài toán tương đương với
2 k 2 + 10 3 k - 2 ≥ 4 k 3 x = 2 k 2 + 10 3 k - 2 ≥ 4 2 k 2 + 10 3 k - 2 ∈ ℤ
Ta có
2 k 2 + 10 3 k - 2 ≥ 4 k 3 x = 2 k 2 + 10 3 k - 2 ≥ 4 ⇔ - 6 k 2 + 8 k + 30 3 k - 2 ≥ 0 2 k 2 - 12 k + 18 3 k - 2 ≥ 0 ⇔ 2 3 < k ≤ 3
Vì k ∈ ℤ nên k ∈ 1 ; 2 ; 3
Với k = 1 suy ra 2 k 2 + 10 3 k - 2 = 12 ∈ Z
Với k = 2 suy ra 2 k 2 + 10 3 k - 2 = 9 2 ∉ 9 2
Với k = 3 suy ra 2 k 2 + 10 3 k - 2 = 4 ∈ Z
Kết hợp với điều kiện ta suy ra x = 4; x = 12
Vậy có 2 giá trị nguyên dương cần tìm
Đáp án C
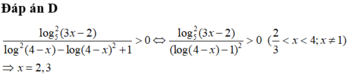



\(a,\)\(xy+3x+2y=6\)
\(\Rightarrow xy+3x+2y+6=6+6\)
\(\Rightarrow x\left(y+3\right)+2\left(y+3\right)=12\)
\(\Rightarrow\left(y+3\right)\left(y+2\right)=12\)
\(TH1\):\(\orbr{\begin{cases}y+3=1\\x+2=12\end{cases}\Rightarrow\orbr{\begin{cases}y=-2\\x=10\end{cases}}}\)
\(TH2\): \(\orbr{\begin{cases}y+3=-1\\x+2=-12\end{cases}\Rightarrow\orbr{\begin{cases}y=-4\\x=-14\end{cases}}}\)
\(TH3\): \(\orbr{\begin{cases}y+3=12\\x+2=1\end{cases}\Rightarrow\orbr{\begin{cases}y=9\\x=-1\end{cases}}}\)
\(TH4\): \(\orbr{\begin{cases}y+3=-12\\x+2=-1\end{cases}\Rightarrow\orbr{\begin{cases}y=-15\\x=-3\end{cases}}}\)
\(TH5\): \(\orbr{\begin{cases}y+3=2\\x+2=6\end{cases}\Rightarrow\orbr{\begin{cases}y=-1\\x=4\end{cases}}}\)
\(TH6\): \(\orbr{\begin{cases}y+3=6\\x+2=2\end{cases}\Rightarrow\orbr{\begin{cases}x=3\\x=0\end{cases}}}\)
\(TH7\): \(\orbr{\begin{cases}y+3=-2\\x+2=-6\end{cases}\Rightarrow\orbr{\begin{cases}y=-5\\x=-8\end{cases}}}\)
\(TH8\)\(:\)\(\orbr{\begin{cases}y+3=-6\\x+2=-2\end{cases}\Rightarrow\orbr{\begin{cases}y=-9\\x=-4\end{cases}}}\)
\(TH9\): \(\orbr{\begin{cases}y+3=3\\x+2=4\end{cases}\Rightarrow\orbr{\begin{cases}y=0\\x=2\end{cases}}}\)
\(TH10\): \(\orbr{\begin{cases}y+3=4\\x+2=3\end{cases}\Rightarrow\orbr{\begin{cases}y=1\\x=1\end{cases}}}\)
\(TH11\): \(\orbr{\begin{cases}y+3=-3\\x+2=-4\end{cases}\Rightarrow\orbr{\begin{cases}y=-6\\x=-6\end{cases}}}\)
\(TH12\): \(\orbr{\begin{cases}y+3=-4\\x+2=-3\end{cases}\Rightarrow\orbr{\begin{cases}y=-7\\x=-5\end{cases}}}\)
KL...
chưa thấy bạn nào làm bài 3 , thì em làm ạ :))
Giả sử x, y là các số nguyên thoă mãn phương trình đã cho .
\(4x+5y=2012\Leftrightarrow5y=2012-4y\Leftrightarrow5y=4\left(503-y\right).\)(1)
Dễ thấy vế phải của (1) chia hết cho 4 \(\Rightarrow5y⋮4\)mà (5;4)=1 nên y chia hết cho 4.
Đặt \(y=4t\left(t\in Z\right)\)thế vào phương trình đầu ta được : \(4x+20t=2012\Leftrightarrow\hept{\begin{cases}x=503-5t\\y=4t\end{cases}.}\)(*)
Thử thay vào các biểu thức của x, y ở (*) ta thấy thỏa mãn
Vậy phương trình có vô số nghiệm \(\left(x;y\right)=\left(503-5t;4t\right)\forall t\in Z.\)