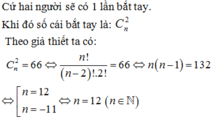Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cứ hai người sẽ có lần bắt tay nên có tất cả ![]() cái bắt tay
cái bắt tay
Theo đầu bài ta có:
C n 2 = 66 ⇔ n ! ( n - 2 ) ! . 2 ! = 66 ⇔ n ( n - 1 ) = 132 ⇔ n = 12 h o ặ c n = - 11 ( l o ạ i ) ⇒ n = 12 ( n ∈ N )
Chọn B.

Đáp án C
Nếu mỗi người đều bắt tay với tất cả thì có C 26 2 cái bắt tay, trong đó có C 13 2 cái bắt tay giữa các bà vợ và 13 cái bắt tay giữa các cặp vợ chồng.
Như vậy theo điều kiện bài toán sẽ có: C 26 2 - C 13 2 - 13 = 234 (cái bắt tay).

Chọn D
Sau khi chia tiền lần đầu tiên sẽ có 8 trường hợp xảy ra như sau:
| Raashan |
Sylvia |
Ted |
| 1 |
1 |
1 |
| 1 |
1 |
1 |
| 2 |
1 |
0 |
| 2 |
0 |
1 |
| 1 |
2 |
0 |
| 0 |
2 |
1 |
| 1 |
0 |
2 |
| 0 |
1 |
2 |
Các số lần lượt là số tiền của mỗi bạn. Có hai trường hợp cho kết quả (1;1;1) đó là Raashan → Sylvia → Ted Raashan hoặc Raashan Ted Sylvia Raashan.
Với mỗi trường hợp cho kết quả (1;1;1) thì lượt chơi tiếp theo sẽ có 1 4 cơ hội để số tiền mỗi người bằng nhau.
Đối với trường hợp một người có 2$, một người có 1$ và người còn lại không có tiền thì lượt chơi thứ hai sẽ có 4 trường hợp xảy ra. Không mất tính tổng quát ta giả sử Raashan có 2$, Sylvia có 1$ và Ted không có tiền, ta có những cách chuyển tiền như sau:
- Raashan ⇆ Sylvia và Ted không nhận được tiền.
Raashan → Sylvia → Ted.
- Raashan → Ted → Sylvia.
- Sylvia → Raashan → Ted.
Như vậy trong 4 khả năng trên chỉ có một khả năng cho kết quả (1;1;1) chiếm tỉ lệ 1 4
Cứ tiếp tục chơi như vậy đến lượt thứ 2019. Khi đó xác suất mỗi người chơi có 1$ là
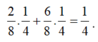

Số cái bắt tay ít nhất đã xảy ra là \(C^2_{20}=20\cdot19:2=190\left(cái\right)\)