Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc ô tô dự định đi quãng đường AB là x (km/h).
Có phương trình: 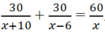
Giải ra được x = 30
Thời gian ô tô dự định đi là 2 giờ.

gọi vận tốc dự định đi quãng đường AB = x km/giờ (x>0)
thời gian dự định đi quãng đường AB = 60/x
--> vận tốc đi nửa đường đầu (đi 30km đầu) = x + 10
thời gian đi nửa đường đầu = 30/(x + 10)
--> vận tốc đi nửa đường sau (đi 30 km sau) = x - 6
thời gian đi nửa đường sau = 30/(x -6)
Theo đề ta có
30/(x + 10) + 30/(x - 6) = 60/x
1/(x + 10) + 1/(x - 6) = 2/x
x(x-6) + x(x+10) = 2(x-6)(x+10)
x^2 - 6x + x^2 +10x = 2(x^2 + 4x - 60)
2x^2 + 4x = 2x^2 + 8x - 120
4x = 120
x = 30 (thỏa)
Vậy thời gian dự định đi quãng đường AB là t = 60/x = 60/30 = 2 giờ

Sửa đề: AB dài 60km
Gọi x(km/h) là vận tốc dự định của ô tô(Điều kiện: x>0)
Thời gian dự định là: \(\dfrac{60}{x}\left(h\right)\)
Thời gian ô tô đi nửa quãng đường đầu là: \(\dfrac{30}{x+10}\left(h\right)\)
Thời gian ô tô đi nửa quãng đường sau là: \(\dfrac{30}{x-6}\left(h\right)\)
Theo đề, ta có phương trình: \(\dfrac{30}{x+10}+\dfrac{30}{x-6}=\dfrac{60}{x}\)
\(\Leftrightarrow\dfrac{30\left(x-6\right)+30\left(x+10\right)}{\left(x+10\right)\left(x-6\right)}=\dfrac{60}{x}\)
\(\Leftrightarrow\dfrac{60x+120}{\left(x+10\right)\left(x-6\right)}=\dfrac{60}{x}\)
\(\Leftrightarrow\dfrac{x\left(60x+120\right)}{x\left(x+10\right)\left(x-6\right)}=\dfrac{60\left(x+10\right)\left(x-6\right)}{x\left(x+10\right)\left(x-6\right)}\)
\(\Leftrightarrow60x^2+120x=60\left(x^2+4x-60\right)\)
\(\Leftrightarrow60x^2+120x-60x^2-240x+3600=0\)
\(\Leftrightarrow-120x=-3600\)
hay x=30(thỏa ĐK)
Vậy: Vận tốc dự định là 30km/h


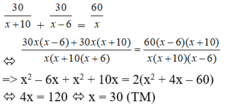
Vậy thời gian dự định đi quãng đường AB là 60 : 30 = 2 giờ
Đáp án cần chọn là D

Đổi : 60m = 0,06km
- Gọi vận tốc dự định đi là x ( km/h, x > 0 )
- Vận tốc thức tế ở hai nửa quãng đường là : x + 10; x - 6 ( km/h )
Theo bài ra ta có : \(\dfrac{0,03}{x+10}+\dfrac{0,03}{x-6}=\dfrac{0,06}{x}\)
\(\Leftrightarrow\dfrac{1}{x+10}+\dfrac{1}{x-6}=\dfrac{2}{x}\)
\(\Leftrightarrow x\left(x-6\right)+x\left(x+10\right)=2\left(x+10\right)\left(x-6\right)\)
\(\Leftrightarrow4x=120\)
\(\Leftrightarrow x=30\) ( TM )
Vậy ...
Gọi vận tốc dự định của ô tô là x(km/h)(Điều kiện: x>0)
Theo đề, ta có phương trình:
\(\dfrac{30}{x+10}+\dfrac{30}{x-6}=\dfrac{60}{x}\)
\(\Leftrightarrow\dfrac{30\left(x-6\right)+30\left(x+10\right)}{\left(x+10\right)\left(x-6\right)}=\dfrac{60}{x}\)
\(\Leftrightarrow\dfrac{30x-180+30x+300}{\left(x+10\right)\left(x-6\right)}=\dfrac{60}{x}\)
\(\Leftrightarrow x\left(60x+120\right)=60\left(x+10\right)\left(x-6\right)\)
\(\Leftrightarrow60x^2+120x=60\left(x^2-6x+10x-60\right)\)
\(\Leftrightarrow60x^2+120x=60x^2+240x-3600\)
\(\Leftrightarrow-120x=-3600\)
hay x=30(thỏa ĐK)
Vậy: Vận tốc dự định là 30km/h

Giải:
Gọi vận tốc dự định đi quãng đường AB = x km/giờ (x>0)
thời gian dự định đi quãng đường AB = 60/x
--> vận tốc đi nửa đường đầu (đi 30km đầu) = x + 10
thời gian đi nửa đường đầu = 30/(x + 10)
--> vận tốc đi nửa đường sau (đi 30 km sau) = x - 6
thời gian đi nửa đường sau = 30/(x -6)
Theo đề ta có
30/(x + 10) + 30/(x - 6) = 60/x
1/(x + 10) + 1/(x - 6) = 2/x
x(x-6) + x(x+10) = 2(x-6)(x+10)
x^2 - 6x + x^2 +10x = 2(x^2 + 4x - 60)
2x^2 + 4x = 2x^2 + 8x - 120
4x = 120
x = 30 (thỏa)
Vậy thời gian dự định đi quãng đường AB là t = 60/x = 60/30 = 2 giờ

Gọi vận tốc ban đầu của người đó là x (km/h; \(x>5\))
Thời gian dự định là \(\dfrac{60}{x}\) (giờ)
Vận tốc lúc sau là x - 5 (km/h)
Thời gian người đó đi trên nửa quãng đường đầu là \(\dfrac{30}{x}\) (giờ)
Thời gian người đó đi trên nửa quãng đường sau là \(\dfrac{30}{x-5}\) (giờ)
Do người đó đến B chậm hơn dự định 1 giờ => ta có phương trình:
\(\dfrac{30}{x}+\dfrac{30}{x-5}=\dfrac{60}{x}+1\)
<=> \(\dfrac{30}{x-5}-\dfrac{30}{x}-1=0\)
<=> \(\dfrac{30x-30\left(x-5\right)-x\left(x-5\right)}{x\left(x-5\right)}=0\)
<=> 30x - 30x + 150 - x2 + 5x = 0
<=> x2 -5x - 150 = 0
<=> (x-15)(x+10) = 0
Mà x > 5
<=> x - 15 = 0
<=> x = 15 (tm)
KL Vận tốc dự định của người đó là 15 km/h
Gọi vận tốc dự định của ô tô là: x ( km/h)
( Điều kiện: x > 4 )
=> Thời gian dự định đi từ A đến B của ô tô là: \(\frac{120}{x}\left(h\right)\)
Nửa đường đầu, vận tốc của ô tô là: x - 4 (km/h)
=> Thời gian đi nửa đường đầu của ô tô là: \(\frac{60}{x-4}\left(h\right)\)
Nửa đường sau, vận tốc của ô tô là: x + 5 (km/h)
=> Thời gian đi nửa đường sau của ô tô là: \(\frac{60}{x+5}\left(h\right)\)
Vì ô tô vẫn đến B với thời gian dự định nên ta có phương trình:
\(\frac{60}{x-4}+\frac{60}{x+5}=\frac{120}{x}\)
\(\Leftrightarrow\frac{60x\left(x+5\right)}{x\left(x-4\right)\left(x+5\right)}+\frac{60x\left(x-4\right)}{x\left(x-4\right)\left(x+5\right)}=\frac{120\left(x-4\right)\left(x+5\right)}{x\left(x-4\right)\left(x+5\right)}\)
\(\Rightarrow60x^2+300x+60x^2-240x=120x^2+120x-2400\)
\(\Leftrightarrow-60x=-2400\)
\(\Leftrightarrow x=40\left(tm\right)\)
Vậy: Vận tốc dự định của ô tô là: 40 km/h
=.= hk tốt!!