Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

https://hoc24.vn/hoi-dap/tim-kiem?id=178370&q=M%E1%BB%99t%20h%C3%ACnh%20thang%20c%C3%A2n%20c%C3%B3%20%C4%91%C3%A1y%20l%E1%BB%9Bn%20d%C3%A0i%202%2C7cm%2C%20c%E1%BA%A1nh%20b%C3%AAn%20d%C3%A0i%201m%2C%20g%C3%B3c%20t%E1%BA%A1o%20b%E1%BB%9Fi%20%C4%91%C3%A1y%20l%E1%BB%9Bn%20v%C3%A0%20c%E1%BA%A1nh%20b%C3%AAn%20c%C3%B3%20s%E1%BB%91%20%C4%91o%20b%E1%BA%B1ng%20600.%20T%C3%ADnh%20%C4%91%E1%BB%99%20d%C3%A0i%20c%E1%BB%A7a%20%C4%91%C3%A1y%20nh%E1%BB%8F
Kẻ AH ⊥CD , BK⊥CD
Xét tam giác vuông AHD và tam giác vuông BKC, có: góc ADH = góc BCK = 600 ; cạnh AH = BK
=> tam giác AHD = tam giác BKC (gcg)
=> DH = KC
Đặt a = DH (a > 0) => AH = √1−x2
Có: Sin60 = AH/AD ➝√3/2 -√1−x2 ➝1−x2=3/4➝x2=1/4➝[x=12(n)
x=−12(l)
=> x = 1/2 hay DH = KC = 1/2
Mặt khác: HK = CD - (DH + KC) = 2,7 - (1/2 + 1/2) = 1,7 (m)
Tứ giác ABCD là hình chữ nhật (góc AHK = góc BKH = ABK = 900) => AB = HK = 1,7 (m)
Vậy AB = 1,7m

Câu 1
X^3+Y3+z^3-3xyz = (x+y+z)(x^2+y^2+z^2 -xy-yz-zx) =0. Nên chỉ có 2 TH
a) TH1: x+y+z = 0 --> x+y=-z; y+z=-x; z+x=-y (1):
Biến đổi P= (x+y)(y+z)(z+x)/xyz (2). Thay (1) vào (2) được P = -xyz/xyz = -1
b) TH2: x^2+y^2+z^2 -xy-yz-zx --> x=y=z. Thay vào biểu thức của P được P = (1+1)(1+1)(1+1)=8
Câu 3
x^2+y^2 >= 2xy
y^2+z^2 >= 2yz
z^2+x^2>=2xz
Cộng 2 vế với vế cuae 3 BDT trên được 2(x^2+y^2+x^2)>=2(xy+yz+zx) --> x^2+y^2+x^2>= xy+yz+zx (1) Dấu = xảy ra khi x=y=z
Mặt khác A=(x+y+z)^2=x^2+y^2+x^2+2(xy+yz+zx)=9. Theo (1) A>=xy+yz+zx+2(xy+yz+zx) = 3(xy+yz+zx)
nên 9>=3(xy+yz+zx) --> 3>=xy+yz+zx. Vậy giá trị lớn nhất của P là 9. Khi đó x=y=z=1

kẻ đg cao AH trong tam giác ADH có D=60 ; DH = AD/2 = 0,5cm
AB = CD - 2DH = 2,7 - 2.0,5 = 1,7cm
bn kẻ đg cao AH và BK thì có phải AH= BK không vì ABCD là ht cân mà
AB = CD - DH - KC = CD - 2DH đúng k?
tam giác AHD vuông tại H mà có góc D =60o nên nó = 1/2 tam giác đều,=> DH = AD/2 = 1/2
bn hiểu rồi chứ

1/
Kẻ AH \(\perp\)CD , \(BK\perp CD\)
Xét tam giác vuông AHD và tam giác vuông BKC, có: góc ADH = góc BCK = 600 ; cạnh AH = BK
=> tam giác AHD = tam giác BKC (gcg)
=> DH = KC
Đặt a = DH (a > 0) => AH = \(\sqrt{1-x^2}\)
Có: Sin60 = \(\frac{AH}{AD}\Rightarrow\frac{\sqrt{3}}{2}=\sqrt{1-x^2}\Rightarrow1-x^2=\frac{3}{4}\Rightarrow x^2=\frac{1}{4}\Rightarrow\left[\begin{array}{nghiempt}x=\frac{1}{2}\left(n\right)\\x=-\frac{1}{2}\left(l\right)\end{array}\right.\)
=> x = 1/2 hay DH = KC = 1/2
Mặt khác: HK = CD - (DH + KC) = 2,7 - (1/2 + 1/2) = 1,7 (m)
Tứ giác ABCD là hình chữ nhật (góc AHK = góc BKH = ABK = 900) => AB = HK = 1,7 (m)
Vậy AB = 1,7m
2/
a/ Cm: tam giác ICD đều:
Trong tam giác ICD : DB vừa là đường phân giác , vừa là đường cao => tam giác ICD là tam giác cân tại D
=> ID = DC (1)
=> DB vừa là đường trung tuyến => BI = BC = 4cm => IC = 4 + 4 = 8cm (2)
Có: góc IAB = IDC (đồng vị) , góc IBA = góc ICD (đồng vị)
mà góc IDC = góc ICD
=> góc IAB = góc IBA => tam giác IAB cân tại I => IA = IB = 4cm
=> ID = IA + AD = 4 + 4 = 8cm (3)
Từ (1), (2), (3) => ID = DC = IC = 8cm hay tam giác IDC đều
b/ Tính chu vi hình thang ABCD:
Vì tam giác ICD đều => tam giác IAB đều => IA = AB = 4cm
ID = DC = 8cm
Vậy chu vi hình thang ABCD : AB + AD + BC + CD = 4 + 4 + 4 + 8 = 20(cm)

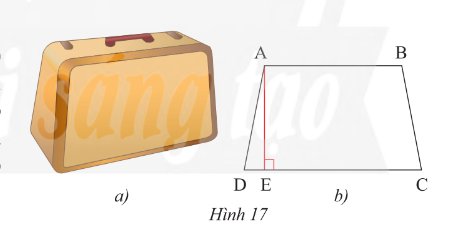
Áp dụng định lý Pythagore vào tam giác vuông \(ADE\) ta có:
\(D{E^2} + A{E^2} = A{D^2}\)
\(D{E^2} = A{D^2} - A{E^2} = {61^2} - {60^2} = 121 = {11^2}\)
\(DE = 11\) (cm)
Độ dài \(AB\) là: \(92 - 11.2 = 70\) (cm)

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)