Question

[C H I I]

1. Cho tam giác ABC. Trên cạnh AB lấy D, trên cạnh AC lấy E sao cho AD/AB = AE/AC

a) Chứng minh: AD/BD = AE/EC

b) Tính BC biết AD = 2cm, BD = 1cm, DE = 3cm.

2. Cho tam giác ABC có AB = 11cm. Lấy D trên đoạn AB sao cho AD = 4cm. Qua D kẻ DE // BC (E thuộc AC).

Biết EC-AE = 1,5cm, BC = 8cm.

a) Tính tỉ số AE: EC

b) Tính các đoạn thẳng AE, DE?

3.Cho hình thang ABCD (AB//CD) Gọi O là giao điểm của AC và BD.

a) Chứng minh: OA.OD = OB.OC

b) Qua O kẻ MN // AB (M ∈ AD, N ∈ BC). Chứng minh O là trung điểm của MN.

MÌNH ĐANG CẦN GẤP, MNG GIÚP VỚI Ạ

Answer 1

[Đào Thu Hiền]

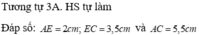
1.

a) Xét ΔABC có \(\frac{AD}{AB}=\frac{AE}{AC}\left(gt\right)\) => DE//BC

=> \(\frac{AD}{BD}=\frac{AE}{EC}\) (đ/lí Ta-lét)

b) Ta có: AB = AD + BD = 2 + 1 = 3 (cm)

Xét ΔABC có DE//BC => \(\frac{AD}{AB}=\frac{DE}{BC}=\frac{2}{3}\) (hệ quả đ/lí Ta-lét)

=> BC = \(\frac{AB.DE}{AD}=\frac{3.3}{2}=4,5\left(cm\right)\)

2.

a) Ta có: BD = AB - AD = 11 - 4 = 7 (cm)

Xét ΔABC có DE//BC (gt), theo đ/lí Ta-lét có: \(\frac{AE}{EC}=\frac{AB}{BD}=\frac{4}{7}\)

b) Ta có: \(\frac{AE}{EC}=\frac{4}{7}\left(cmt\right)\) => \(\frac{AE}{EC-AE}=\frac{4}{7-4}\Rightarrow\frac{AE}{1,5}=\frac{4}{3}\)

=> AE = \(\frac{4.1,5}{3}=2\left(cm\right)\)

Xét ΔABC có DE//BC (gt) => \(\frac{AD}{AB}=\frac{DE}{BC}\) (hệ quả đ/lí Ta-lét)

=> DE = \(\frac{AD.BC}{AB}=\frac{4.8}{11}=\frac{32}{11}\left(cm\right)\)

3.

a) Xét ΔOCD có AB//CD (gt), theo đ/lí Ta-lét có: \(\frac{OC}{OA}=\frac{OD}{OB}\)

=> OA.OD = OB.OC

b) Do \(\frac{OC}{OA}=\frac{OD}{OB}\)(cmt) => \(\frac{OC}{OA+OC}=\frac{OD}{OB+OD}\Rightarrow\frac{OC}{AC}=\frac{OD}{BD}\) (1)

Do MN//AB => OM//AB; ON//AB

Xét ΔABD có OM//AB (cmt) => \(\frac{OM}{AB}=\frac{OD}{BD}\) (hệ quả đ/lí Ta-lét) (2)

Xét ΔABC có ON//AB (cmt) => \(\frac{ON}{AB}=\frac{OC}{AC}\) (hệ quả đ/lí Ta-lét) (3)

Từ (1), (2), (3) => \(\frac{OM}{AB}=\frac{ON}{AB}\) => OM = ON