Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: OB=OC
AB=AC
Do đó: AO là đường trung trực của BC
=>A,O,H thẳng hàng
hay AD là đừog kính
b: Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đo: ΔACD vuông tại C
hay góc ACD=90 độ

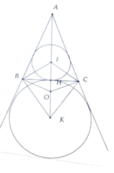
a, Sử dụng tính chất phân giác trong và phân giác ngoài tại 1 điểm ta có:
I B K ^ = I C K ^ = 90 0
=> B, C, I, K ∈ đường tròn tâm O đường kính IK
b, Chứng minh
I
C
A
^
=
O
C
K
^
từ đó chứng minh được
O
C
A
^
=
90
0
Vậy AC là tiếp tuyến của (O)
c, Áp dụng Pytago vào tam giác vuông HAC => AH=16cm. Sử dụng hệ thức lượng trong tam giác vuông COA => OH=9cm,OC=15cm
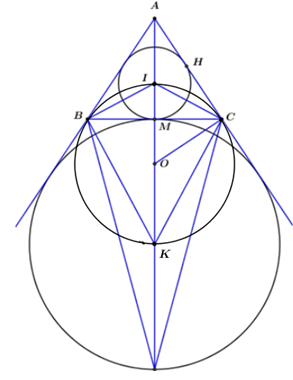
a) CMR: 4 điểm B, I, C, K cùng thuộc (O).
Vì I là tâm đường tròn ngoại tiếp tam giác ABC nên IC là phân giác trong của góc C.
Vì K là tâm đường tròn ngoại tiếp tam giác ABC của góc A nên CK là phân giác ngoài của góc C.
Theo tính chất phân giác trong và phân giác ngoài ta có IC vuông CK nên ∠ICK=90
Chứng minh hoàn toàn tương tự ta có: ∠IBK=90
Xét tứ giác BICK ta có: ∠IBK+∠ICK=90+90=180
⇒BICK là tứ giác nội tiếp (tứ giác có tổng hai góc đối diện bằng 180)
Do O là trung điểm của IK nên theo tính chất trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền thì OC = OI = OK.
Vậy O là tâm đường tròn ngoại tiếp tứ giác IBKC.
b) CMR: AC là tiếp tuyến của (O).
Ta có : Tam giác IOC cân tại O nên : ∠OIC=∠OCI.
Mặt khác, theo tính chất góc ngoài của tam giác ta có :
∠OIC=∠IAC+∠ACI=1/2∠BAC+1/2∠ACB=1/2∠BAC+1/2∠ABC
⇒∠ICO+∠ICA=1/2∠BAC+1/2∠ABC+1/2∠ACB=12.180=90 ⇒OC⊥CA.
Do đó AC là tiếp tuyến của (O) tại C (đpcm).
c) Tính tổng diện tích các hình viên phân giới hạn bởi các cung nhỏ CI, IB, BK, KC và các dây cung tương ứng của (O) biết AB = 20, BC = 24.
Gọi diện tích hình cần tính là S, diện tích hình tròn (O) là S’, gọi giao điểm BC và IK là M.
Ta có ngay :
S = S′−S (ICKB) =π.IO2−S (IBK)−S (IKC)
= π.IK2/4 −(BM.IK)/2−(CM.IK)/2
=πIK2/4 − (BC.IK)/2
Ta có :
S (ABC) = 1/2 (AM.BC) = (AB+BC+CA) /2 .IM
⇔√(AB2−BM2 ) .24 = (AB+BC+CA).IM
⇔√[202−(24/2)2 ]. 24= (20.2+24).IM⇔IM=6.
Áp dụng hệ thức lượng trong tam giác IBM vuông tại B có đường cao BM ta có :
BM2=IM.MK ⇔MK=BM2/IM=122/6=24
⇒IM=IM+MK=6+24=30.
⇒S= 1/4(π.IK2)−1/2 BC.IK =1/4 π.302 −1/2(24.30 ) =225π−360 ≈346,86 (dvdt)

Đáp án là C
Tam giác ABC có:
A B 2 + A C 2 = 12 2 + 16 2 = 400 = B C 2
⇒ ΔABC vuông tại A
⇒ Tâm đường tròn ngoại tiếp tam giác ABC là trung điểm của BC
⇒ Bán kính = 10 cm

Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=5^2+12^2=169\)
hay BC=13cm
Ta có: ΔABC vuông tại A
nên bán kính đường tròn ngoại tiếp ΔABC là một nửa của cạnh huyền BC
hay \(R=\dfrac{BC}{2}=\dfrac{13}{2}=6.5\left(cm\right)\)
Bài 2:
Ta có: ABCD là hình thang cân
nên A,B,C,D cùng thuộc 1 đường tròn\(\left(đl\right)\)
hay bán kính đường tròn ngoại tiếp ΔABC cũng là bán kính đường tròn ngoại tiếp tứ giác ABCD
Xét ΔABC có
\(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Suy ra: Bán kính của đường tròn ngoại tiếp tứ giác ABCD là \(R=\dfrac{BC}{2}=10\left(cm\right)\)