Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu hỏi của Trần Thị Thùy Linh 2004 - Toán lớp 8 - Học toán với OnlineMath
EM tham khảo nhé!

Bài 1:
$a^3+b^3+c^3=3abc$
$\Leftrightarrow (a+b)^3-3ab(a+b)+c^3-3abc=0$
$\Leftrightarrow [(a+b)^3+c^3]-[3ab(a+b)+3abc]=0$
$\Leftrightarrow (a+b+c)[(a+b)^2-c(a+b)+c^2]-3ab(a+b+c)=0$
$\Leftrightarrow (a+b+c)[(a+b)^2-c(a+b)+c^2-3ab]=0$
$\Leftrightarrow (a+b+c)(a^2+b^2+c^2-ab-bc-ac)=0$
$\Rightarrow a+b+c=0$ hoặc $a^2+b^2+c^2-ab-bc-ac=0$
Xét TH $a^2+b^2+c^2-ab-bc-ac=0$
$\Leftrightarrow 2(a^2+b^2+c^2)-2(ab+bc+ac)=0$
$\Leftrightarrow (a-b)^2+(b-c)^2+(c-a)^2=0$
$\Rightarrow a-b=b-c=c-a=0$
$\Leftrightarrow a=b=c$
Vậy $a^3+b^3+c^3=3abc$ khi $a+b+c=0$ hoặc $a=b=c$
Áp dụng vào bài:
Nếu $a+b+c=0$
$A=\frac{-c}{c}+\frac{-b}{b}+\frac{-a}{a}=-1+(-1)+(-1)=-3$
Nếu $a=b=c$
$P=\frac{a+a}{a}+\frac{b+b}{b}+\frac{c+c}{c}=2+2+2=6$

Ta có
( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 = a 3 + b 3 + 3 a b ( a + b ) = > a 3 + b 3 = ( a + b ) 3 – 3 a b ( a + b )
Từ đó
B = a 3 + b 3 + c 3 – 3 a b c = ( a + b ) 3 – 3 a b ( a + b ) + c 3 – 3 a b c = [ ( a + b ) 3 + c 3 ] – 3 a b ( a + b + c ) = ( a + b + c ) [ ( a + b ) 2 – ( a + b ) c + c 2 ] – 3 a b ( a + b + c )
Mà a + b + c = 0 nên
B = 0 . [ ( a + b ) 2 – ( a + b ) c + c 2 ] – 3 a b . 0 = 0
Vậy B = 0
Đáp án cần chọn là: A

\(a+b+c=1\)
\(\Leftrightarrow\left(a+b+c\right)^3=1\)
\(\Leftrightarrow a^3+b^3+c^3+3\left(a+b\right)\left(b+c\right)\left(c+a\right)=1\)
\(\Leftrightarrow1+3\left(a+b\right)\left(b+c\right)\left(c+a\right)=1\)'
\(\Leftrightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a+b=0\\b+c=0\\c+a=0\end{matrix}\right.\)
Không mất tính tổng quát, giả sử \(a+b=0\), các trường hợp còn lại làm tương tự.
Khi đó từ \(a+b+c=1\) suy ra \(c=1\) (thỏa mãn). Thế thì \(T=0^{2023}+0^{2023}+1^{2023}=1\).
Như vậy \(T=1\)

1.
\(a+b+c=0\)
\(\Rightarrow\left(a+b+c\right)^2=0\)
\(\Rightarrow a^2+b^2+c^2+2ab+2bc+2ca=0\)
\(\Rightarrow a^2+b^2+c^2=-2\left(ab+bc+ca\right)\)
Ta có:
\(\dfrac{\left(a+2b\right)^2+\left(b+2c\right)^2+\left(c+2a\right)^2}{\left(a-2b\right)^2+\left(b-2c\right)^2+\left(c-2a\right)^2}\)
\(=\dfrac{a^2+4b^2+4ab+b^2+4c^2+4bc+c^2+4a^2+4ca}{a^2+4b^2-4ab+b^2+4c^2-4bc+c^2+4a^2-4ca}\)
\(=\dfrac{5\left(a^2+b^2+c^2\right)+4\left(ab+bc+ca\right)}{5\left(a^2+b^2+c^2\right)-4\left(ab+bc+ca\right)}\)
\(=\dfrac{-10\left(ab+bc+ca\right)+4\left(ab+bc+ca\right)}{-10\left(ab+bc+ca\right)-4\left(ab+bc+ca\right)}\)
\(=\dfrac{-6}{-14}=\dfrac{3}{7}\)
b.
\(a^3+b^3+c^3=3abc\)
\(\Leftrightarrow a^3+b^3+3ab\left(a+b\right)-3ab\left(a+b\right)+c^3-3abc=0\)
\(\Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b+c\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(\left(a+b\right)^2-c\left(a+b\right)+c^2\right)-3abc\left(a+b+c\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)=0\)
\(\Leftrightarrow a^2+b^2+c^2-ab-bc-ca=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-b=0\\b-c=0\\c-a=0\end{matrix}\right.\) \(\Leftrightarrow a=b=c\)
\(\Rightarrow\dfrac{ab+2bc+3ca}{3a^2+4b^2+5c^2}=\dfrac{a^2+2a^2+3a^2}{3a^2+4a^2+5a^2}=\dfrac{6}{12}=\dfrac{1}{2}\)
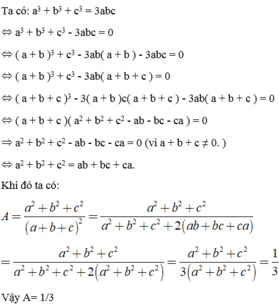
a(a-b)=0 +b(b-c)+c(c-a)=0 suy ra (a-b)2+(b-c)2+(c-a)2=0 suy ra a=b=c
Thay vào A ta đc min A=\(\frac{17}{4}\) tại a=b=c=\(\frac{1}{2}\)
Từ giả thiết => a = 0 hoặc a = b
* TH1: a = 0
b(b-c)+c(c-a)=0 <=> b(b-c)+c2=0 <=> b2 -bc + c2 =0 <=> \(\left(b-\frac{c}{2}\right)^2+\frac{3c^2}{4}=0\)
Điều này xảy ra khi và chỉ khi b - c/2 =0 và c = 0 => b = c = 0
Vậy a = b = c = 0 => A = 5
* TH2: a = b
b(b-c)+c(c-a)=0 <=> b(b-c)+c(c-b)=0 <=> b2 - 2bc + c2 =0 <=> (b-c)2 =0=> b = c
Vậy a =b=c => A = a3 + a3 +a3 - 3a3 + 3a2 - 3a + 5
= 3a2 - 3a + 5 = (3a2 - 3a + 3/4) + 17/4 = 3. (a-1/2)2 + 17/4
Để A nhỏ nhất => a -1/2 =0 => a = 1/2 => Amin = 17/4
17/4 < 5 => Vậy Amin = 17/4 khi a = b = c = 1/2