Đặt \(P=\left(a+b\right)\left(b+c\right)\left(c+a\right)\)

 Trước tiên ta sẽ chứng minh \(P\) chẵn.

 Ta thấy rằng một số nguyên thì hoặc là số chẵn, hoặc là số lẻ. Tuy nhiên, ta có tới 3 số nguyên a, b, c. Điều này có nghĩa là sẽ tồn tại ít nhất 2 số trong 3 số a, b, c có cùng tính chẵn lẻ (nguyên lý Dirichlet). Khi đó tổng của 2 số này là một số chẵn \(\Rightarrow\) P chẵn.

 Ta chứng minh \(P⋮3\)

 Nếu trong 3 số a, b, c có ít nhất một số chia hết cho 3, không mất tính tổng quát, giả sử số đó là a. Khi đó vì \(a,abc,a+b+c+abc\) đều chia hết cho 3 nên \(b+c⋮3\) \(\Rightarrow P⋮3\)

 Nếu trong 3 số a, b, c không có số nào chia hết cho 3 thì sẽ có 2 trường hợp:

 TH1: Cả 3 số này khi chia cho 3 có cùng số dư.

  Khi đó \(a+b+c⋮3\) trong khi \(abc⋮̸3\Rightarrow a+b+c+abc⋮̸3\), không thỏa mãn.

 TH2: 3 số a, b, c chia cho 3 không có cùng số dư. Khi đó tồn tại một số chia 3 dư 1 và một số chia 3 dư 2. Tổng của 2 số này sẽ chia hết cho 3 \(\Rightarrow P⋮3\)

 Vậy \(P⋮3\)

 Ta có \(P⋮2,P⋮3\) và \(ƯCLN\left(2,3\right)=1\) nên \(P⋮6\). Ta có đpcm.

\(a\) \(\Rightarrow b+c⋮3\)

12 \(⋮\) 2n  (n \(\ne\) 0; n \(\in\) Z)

       6 ⋮ n 

 n \(\in\) Ư(6) = {- 6;  -3; -2; -1; 1; 2; 3; 6}

Vậy n \(\in\) {-6; -3; -2;  -1; 1; 2; 3; 6}

A = \(\dfrac{5x-2}{x+2}\) (\(x\ne\) - 2;  0 ≤ \(x\in\)  Z)

A = \(\dfrac{5x-2}{x+2}\) \(\in\) Z ⇔ 5\(x\) - 2 ⋮ \(x+2\) 

          5\(x\) + 10 - 12 ⋮ \(x+2\)

          5(\(x+2\)) - 12 ⋮ \(x+2\)

                12 \(⋮\) \(x+2\) 

            \(x+2\) \(\in\) Ư(12) = {-12; - 6; -4; -3; -2; -1; 1; 2; 3; 4; 6; 12}

             \(x\) \(\in\) {-14; -8; -6; - 5; -4; -3; -1; 0; 1; 2; 4; 10}

   Vì 0≤ \(x\) \(\in\) Z nên \(x\) \(\in\) {0; 1; 2; 4; 10}

Vậy \(x\) \(\in\) {0; 1; 2; 4; 10}

                         34 cm = 0,34 cm 

Nửa chu vi của cái khung hình chữ nhật là: 1,68 : 2 = 0,84 (m)

Chiều dài của cái khung hình chữ nhật là: 0,84 - 0,34 = 0,5 (m)

Đáp số: 

b, 36 cm = 0,36 m

    Chiều dài của cái khung hình chữ nhật là: 0,36 : \(\dfrac{3}{5}\) = 0,6 (m)

Chiều dài của sợi dây thép là: (0,36 + 0,6) x 2 = 1,92 (m)

Đáp số: 1,92 m

         Đây là toán nâng cao chuyên đề bài toán tính tuổi, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, olm sẽ hướng dẫn các em giải chi tiết dạng này bằng sơ đồ đoạn thẳng như sau: 

                                     Giải:

Tổng số tuổi của ba ông cháu hiện nay là:

          100 - 9 = 91 (tuổi)

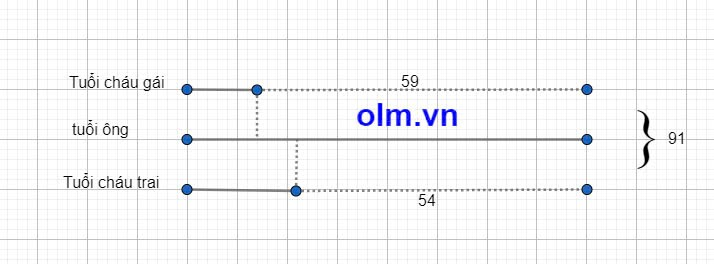
Coi tuổi ông hiện nay là một phần ta có sơ đồ:

Theo sơ đồ ta có:

Tuổi ông hiện nay là: (91 + 54 + 59) : 3 = 68 (tuổi)

Tuổi cháu gái hiện nay là: 68 -  59 = 9 (tuổi)

Tuổi cháu trai hiện nay là: 68 - 54 = 14 (tuổi)

Đáp số: Tuổi ông hiện nay là: 68 (tuổi)

              Tuổi cháu gái hiện nay là: 9 tuổi

              Tuổi trai hiện nay là: 14 tuổi

\(x\) \(\times\) 8,5  - 44 > 20

\(x\) \(\times\) 8,5  > 20 + 44

\(x\) \(\times\) 8,5 > 64

\(x\)           > 64 : 8,5

\(x\)          > \(\dfrac{128}{17}\)

\(x\)          > 7\(\dfrac{9}{17}\)

Vì 7\(\dfrac{9}{17}\) < 8; 9; 10; 11; 12;...

Vậy số tự nhiên nhỏ nhất lớn hơn 7\(\dfrac{9}{17}\) là 8

Vậy \(x=8\) 

\(\text{34,75 x 120 - 34,75 x 19 - 34,75}\)

\(=34,75.\left(120-19-1\right)\)

\(=34,75.100\)

\(=3475\)

học tốt

\(34,75\times120-34,75\times19-34,75\)

\(=34,75\times120-34,75\times19-34,75\times1\)

\(=34,75\times\left(120-19-1\right)\)

\(=34,75\times100\)

\(=3475\)

   42,5 \(\times\) 34,75  + 4,25 \(\times\) 652,5

= 4,25 x 347,5 + 4,25 x 652,5

= 4,25 x (347,5 + 652,5)

= 4,25 x 1000

= 4250

4,358

      Đây là toán nâng cao chuyên đề dãy số có quy luật, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau: 

                                 Giải: 

A = \(\dfrac{1}{6}\) + \(\dfrac{1}{18}\) + \(\dfrac{1}{36}\) + \(\dfrac{1}{60}\) + \(\dfrac{1}{90}\) + ... + \(\dfrac{1}{216}\) + \(\dfrac{1}{270}\)

A = \(\dfrac{1}{3}\) \(\times\) (\(\dfrac{1}{2}\) + \(\dfrac{1}{6}\) + \(\dfrac{1}{12}\) + \(\dfrac{1}{20}\) + \(\dfrac{1}{30}\) + .. + \(\dfrac{1}{72}\) + \(\dfrac{1}{90}\)) 

A = \(\dfrac{1}{3}\) \(\times\) (\(\dfrac{1}{1\times2}\) + \(\dfrac{1}{2\times3}\) + \(\dfrac{1}{3\times4}\) + \(\dfrac{1}{4\times5}\) + ... + \(\dfrac{1}{8\times9}\) + \(\dfrac{1}{9\times10}\)

A = \(\dfrac{1}{3}\) x (\(\dfrac{1}{1}-\dfrac{1}{2}\) + \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) + .. + \(\dfrac{1}{8}-\dfrac{1}{9}\) + \(\dfrac{1}{9}-\dfrac{1}{10}\))

A = \(\dfrac{1}{3}\) x (\(\dfrac{1}{1}\) - \(\dfrac{1}{10}\))

A = \(\dfrac{1}{3}\) x \(\dfrac{9}{10}\)

A = \(\dfrac{3}{10}\) < 8 

Vậy A = \(\dfrac{1}{6}\) + \(\dfrac{1}{18}\) + \(\dfrac{1}{36}\) + ... + \(\dfrac{1}{216}\) + \(\dfrac{1}{270}\) < 8