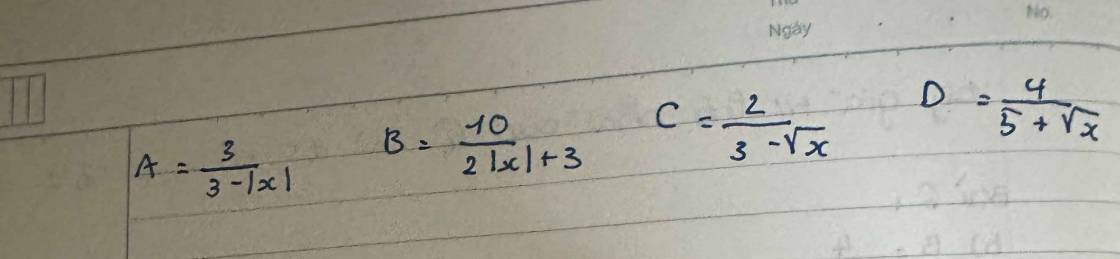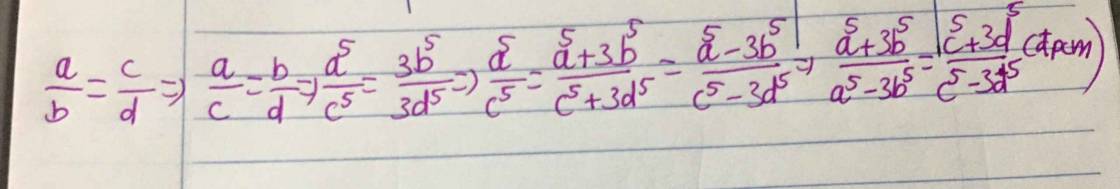Số người công nhân cùng làm khi người quản lí cho vào là :

                 3+4=7(người)

Cần số ngày để lắp rắp xong số linh kiện đó là :

               3.14:7=6(ngày)

                             đs...

Số người công nhân cùng làm khi người quản lí cho vào là :

                 3+4=7(người)

Cần số ngày để lắp rắp xong số linh kiện đó là :

               3.14:7=6(ngày)

                             đáp số: 6 ngày

hình lăng trụ đứng tam giác 

dễ quá

Hình trụ tam giác nha bạn ^^

| x-2| = 5

  \(\left[{}\begin{matrix}x-2=5\\x-2=-5\end{matrix}\right.\)

\(\left[{}\begin{matrix}x=5+2\\x=-5+2\end{matrix}\right.\)

 \(\left[{}\begin{matrix}x=7\\x=-3\end{matrix}\right.\)

x       =5+2

x       =7

A=1(2-1)+2(3-1)+3(4-1)+4(5-1)+...+98(99-1)=

=1.2+2.3+3.4+4.5+...+98.99-(1+2+3+...+98)

Đặt B=1.2+2.3+3.4+...+98.99 và C=1+2+3+...+98

C là tổng của các số lập thành cấp số cộng

3B=1.2.3+2.3.3+3.4.3+...+98.99.3=

=1.2.3+2.3.(4-1)+3.4.(5-2)+...+98.99(100-97)=

=1.2.3-1.2.3+2.3.4-2.3.4+3.4.5-....-97.98.99+98.99.100=98.99.100

B=98.33.100

A=B+C

\(\dfrac{x}{y}=\dfrac{4}{5}\) ⇒ \(\dfrac{x}{4}=\dfrac{y}{5}\) ⇒ \(\dfrac{x+y}{4+5}\) = \(\dfrac{-45}{9}\) = -5

⇒ x = -5.4 = -20; y = -5.5 = - 25

$\genfrac{}{}{0ex}{}{x}{y}=\genfrac{}{}{0ex}{}{4}{5}$ ⇒ $\genfrac{}{}{0ex}{}{x}{4}=\genfrac{}{}{0ex}{}{y}{5}$ ⇒ $\genfrac{}{}{0ex}{}{x+y}{4+5}$ = $\genfrac{}{}{0ex}{}{-45}{9}$ = -5

⇒ x = -5.4 = -20; y = -5.5 = - 25

Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=t\) suy ra \(a=bt,c=dt\).

\(\dfrac{a^5+3b^5}{a^5-3b^5}=\dfrac{\left(bt\right)^5+3b^5}{\left(bt\right)^5-3b^5}=\dfrac{b^5\left(t^5+3\right)}{b^5\left(t^5-3\right)}=\dfrac{t^5+3}{t^5-3}\)

\(\dfrac{c^5+3d^5}{c^5-3d^5}=\dfrac{\left(dt\right)^5+3d^5}{\left(dt\right)^5-3d^5}=\dfrac{d^5\left(t^5+3\right)}{d^5\left(t^5-3\right)}=\dfrac{t^5+3}{t^5-3}\)

Suy ra đpcm.

\(\left(\dfrac{1}{9}\right)^3.\)\(\left(\dfrac{21}{7}\right)^4\).\(\left(\dfrac{-16}{5}\right)^2\)

= \(\dfrac{1}{729}\)    .    \(81\)     .   \(\dfrac{256}{25}\)

= \(\dfrac{1}{9}.\dfrac{256}{25}\) = \(\dfrac{256}{225}\)

C = 1.5 - | x + 2,1| 

| x + 2,1| ≥ 0 ⇔-| x +2,1| ≤ 0 ⇔ C = 1.55 - | x+2,1| ≤ 1,5

⇔ C(max) = 1.5 = 5 ⇔ x = -2,1

D = - 5,7 -| 2,7 - x| 

| 2,7 -x| ≥ 0 ⇔ -| 2,7 -x| ≤ 0 ⇔ D ≤ -5,7

 ⇔ D(max) = -5,7 ⇔ x = 2,7

A = -| x + 8/139| + 141/272

| x + 8/139| ≥ 0 ⇔ -| x + 8/139|  ≤ 0 ⇔ A ≤ 141/272

⇔A(max) = 141/272 ⇔ x = -8/139

C = 1.5 - | x + 2,1| 

| x + 2,1| ≥ 0 ⇔-| x +2,1| ≤ 0 ⇔ C = 1.55 - | x+2,1| ≤ 1,5

⇔ C(max) = 1.5 = 5 ⇔ x = -2,1

D = - 5,7 -| 2,7 - x| 

| 2,7 -x| ≥ 0 ⇔ -| 2,7 -x| ≤ 0 ⇔ D ≤ -5,7

 ⇔ D(max) = -5,7 ⇔ x = 2,7

A = -| x + 8/139| + 141/272

| x + 8/139| ≥ 0 ⇔ -| x + 8/139|  ≤ 0 ⇔ A ≤ 141/272

⇔A(max) = 141/272 ⇔ x = -8/139