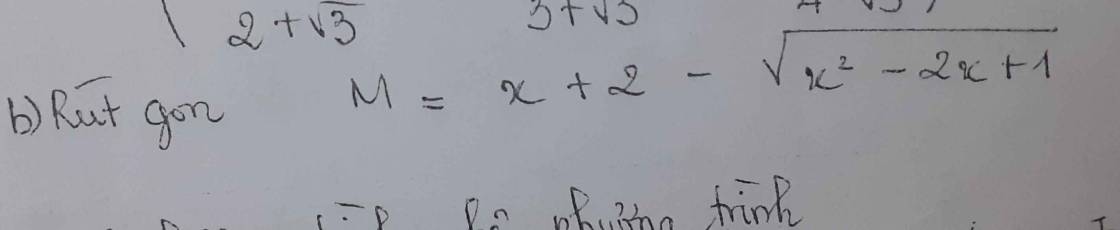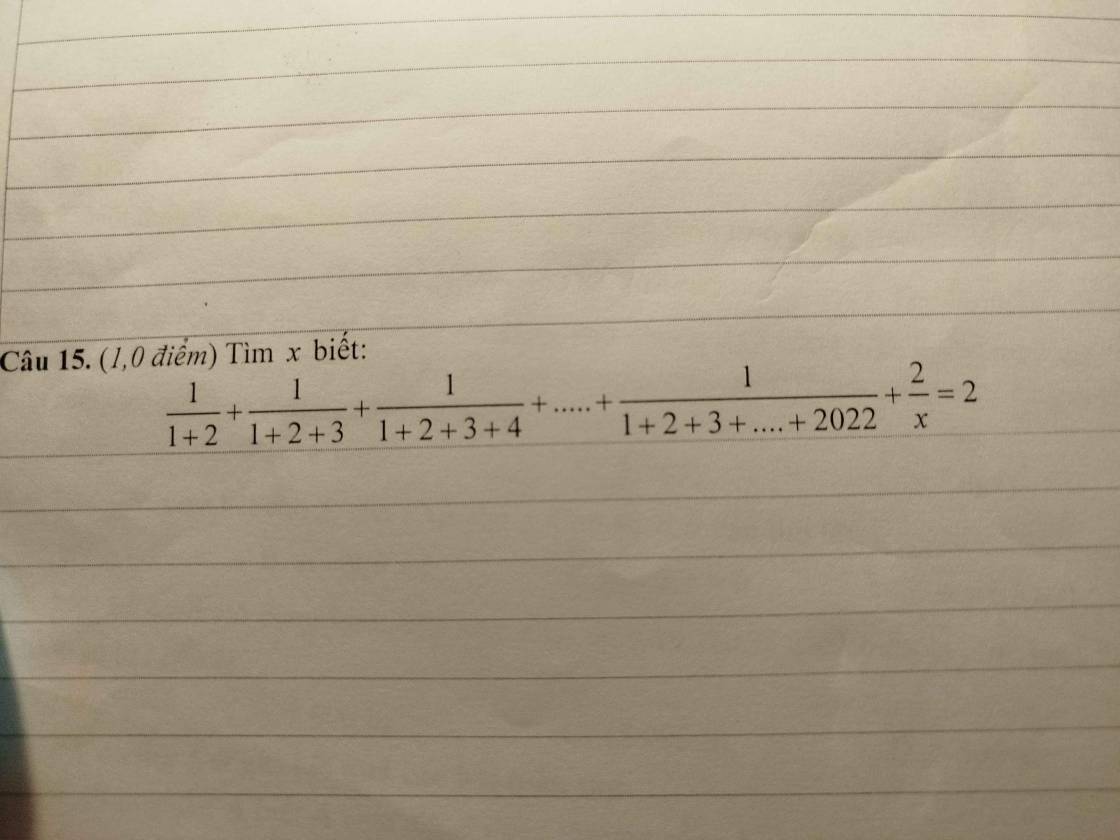mà thui bạn thì tao giúp

450x0,45+1,5x30x3+5x9x2,5

=45x(10x0,45)+1,5x30x3+5x9x2,5

=45x4,5+45x3+45x2,5

=45x(3+45+2,5)

=45x10

=450

Lần sao tự làm nghe

quỳnh ơi cái cách ở 9 với 2,5 là j

a: Xét (O) có

ΔBDC nội tiếp

BC là đường kính

Do đó: ΔBDC vuông tại D

=>CD\(\perp\)AB tại D

Xét (O) có

ΔBEC nội tiếp

BC là đường kính

Do đó: ΔBEC vuông tại E

=>BE\(\perp\)AC tại E

Xét ΔABC có

BE,CD là các đường cao

BE cắt CD tại H

Do đó: H là trực tâm của ΔABC

=>AH\(\perp\)BC tại F

Xét tứ giác HECF có \(\widehat{HEC}+\widehat{HFC}=90^0+90^0=180^0\)

nên HECF là tứ giác nội tiếp

=>\(\widehat{HEF}=\widehat{HCF}\)

b: Xét tứ giác ADHE có \(\widehat{ADH}+\widehat{AEH}=90^0+90^0=180^0\)

nên ADHE là tứ giác nội tiếp

=>\(\widehat{DEH}=\widehat{DAH}\)

mà \(\widehat{HEF}=\widehat{HCF}\)

và \(\widehat{DAH}=\widehat{HCF}\left(=90^0-\widehat{ABC}\right)\)

nên \(\widehat{DEB}=\widehat{FEB}\)

=>EB là phân giác của góc DEF

Bài 1:

\(B=\left(\dfrac{178}{179}+\dfrac{179}{180}+\dfrac{180}{181}\right)\times\left(\dfrac{80}{56}-\dfrac{15}{12}:\dfrac{7}{8}\right)\)

\(=\left(\dfrac{178}{179}+\dfrac{179}{180}+\dfrac{180}{181}\right)\times\left(\dfrac{10}{7}-\dfrac{5}{4}\times\dfrac{8}{7}\right)\)

\(=\left(\dfrac{178}{179}+\dfrac{179}{180}+\dfrac{180}{181}\right)\times\left(\dfrac{10}{7}-\dfrac{10}{7}\right)\)

=0

Bài 2:

Tổng của hai số là 77x2=154

Nếu viết thêm vào bên phải của số thứ nhất một chữ số 0 thì được số thứ hai thì có nghĩa là số thứ hai bằng 10 lần số thứ nhất

Số thứ hai là 154:11x10=140

Số thứ nhất là 154-140=14

ĐKXĐ: \(\left\{{}\begin{matrix}x\ne0\\y\ne0\end{matrix}\right.\)

\(\left\{{}\begin{matrix}\dfrac{2}{3x}+\dfrac{4}{5y}=7\\\dfrac{3}{4x}-\dfrac{2}{5y}=3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{2}{3x}+\dfrac{4}{5y}=7\\\dfrac{6}{4x}-\dfrac{4}{5y}=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{3x}+\dfrac{6}{4x}=7+6\\\dfrac{2}{3x}+\dfrac{4}{5y}=7\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{2}{3x}+\dfrac{3}{2x}=13\\\dfrac{2}{3x}+\dfrac{4}{5y}=7\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{1}{x}\left(\dfrac{2}{3}+\dfrac{3}{2}\right)=13\\\dfrac{2}{3x}+\dfrac{4}{5y}=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}\cdot\dfrac{13}{6}=13\\\dfrac{2}{3x}+\dfrac{4}{5y}=7\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{1}{x}=13:\dfrac{13}{6}=6\\\dfrac{2}{3x}+\dfrac{4}{5y}=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{6}\\\dfrac{4}{5y}=7-\dfrac{2}{3x}=7-\dfrac{2}{3\cdot\dfrac{1}{6}}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=\dfrac{1}{6}\\\dfrac{4}{5y}=7-\dfrac{2}{\dfrac{1}{2}}=7-2\cdot2=3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=\dfrac{1}{6}\\5y=\dfrac{4}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{6}\\y=\dfrac{4}{15}\end{matrix}\right.\left(nhận\right)\)

M = x + 2 - √(x² - 2x + 1)

= x + 2 - √(x - 1)²

= x + 2 - |x - 1| (1)

Với x ≥ 1, ta có:

(1) = x + 2 - x + 1

= 3

Với x < 1, ta có:

M = x + 2 - 1 + x 

= 2x + 1

Bạn Bình có số cái kẹo là:

       (48-12):2=18(cái)

Bạn An có số cái kẹo là:

            48-18=30(cái)

                     Đáp số: Bạn Bình:18 cái kẹo

                                   Bạn An:30 cái kẹo

    Bổ sung cho @ Vu Duy.

    Sơ đồ đoạn thẳng: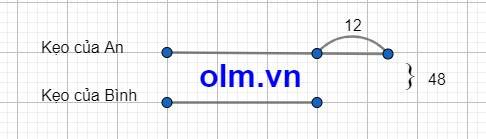 

D.9cm nhé!

Giải thích :

Hình lục giác điều được ghép lại từ 6 hình tam giác đều nên:

Độ dài cạnh của tam giác đều là:

18:2=9(cm)

Mà cạnh của hình tam giác đều cùng là cạnh của hình lục giác đều

=>Độ dài cạnh của hình lục giác đều có đường chéo chính dài 18 cm là :9 cm

Bạn nên viết lại đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người đọc hiểu đề của bạn hơn nhé.

\(\dfrac{1}{1+2}+\dfrac{1}{1+2+3}+...+\dfrac{1}{1+2+3+...+2022}+\dfrac{2}{x}=2\)

=>\(\dfrac{1}{2\text{x}\dfrac{3}{2}}+\dfrac{1}{3\text{x}\dfrac{4}{2}}+...+\dfrac{1}{2022\text{x}\dfrac{2023}{2}}+\dfrac{2}{x}=2\)

=>\(\dfrac{2}{2\text{x}3}+\dfrac{2}{3\text{x}4}+...+\dfrac{2}{2022\text{x}2023}+\dfrac{2}{x}=2\)

=>\(\dfrac{1}{2\text{x}3}+\dfrac{1}{3\text{x}4}+...+\dfrac{1}{2022\text{x}2023}+\dfrac{1}{x}=1\)

=>\(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2022}-\dfrac{1}{2023}+\dfrac{1}{x}=1\)

=>\(\dfrac{1}{2}-\dfrac{1}{2023}+\dfrac{1}{x}=1\)

=>\(\dfrac{1}{x}=1-\dfrac{1}{2}+\dfrac{1}{2023}=\dfrac{1}{2}+\dfrac{1}{2023}=\dfrac{2025}{4046}\)

=>\(x=\dfrac{4046}{2025}\)

\(\dfrac{1}{1+2}\) + \(\dfrac{1}{1+2+3}\) + ... + \(\dfrac{1}{1+2+3+4+...+2022}\) + \(\dfrac{2}{x}\) = 2

\(\dfrac{1}{\left(1+2\right)\times2:2}\) + \(\dfrac{1}{\left(1+3\right)\times3:2}\)+ ... + \(\dfrac{1}{\left(1+2022\right)\times2022:2}\) + \(\dfrac{2}{x}\) = 2

\(\dfrac{2}{2\times3}\) + \(\dfrac{2}{3\times4}\) + ... + \(\dfrac{2}{2022\times2023}\) + \(\dfrac{2}{x}\) = 2

2 x (\(\dfrac{1}{2\times3}\) + \(\dfrac{1}{3\times4}\) + ... + \(\dfrac{1}{2022\times2023}\)) + \(\dfrac{2}{x}\) = 2

2 \(\times\) (\(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2022}-\dfrac{1}{2023}\)) + \(\dfrac{2}{x}\) = 2

2 \(\times\) (\(\dfrac{1}{2}\) - \(\dfrac{1}{2023}\)) + \(\dfrac{2}{x}\) = 2

2 x \(\dfrac{1011}{2023}\) + \(\dfrac{2}{x}\)  = 2

    \(\dfrac{2021}{2023}\)  +  \(\dfrac{2}{x}\) = 2

                   \(\dfrac{2}{x}\) = 2 - \(\dfrac{2021}{2023}\)

                    \(\dfrac{2}{x}\) = \(\dfrac{2025}{2023}\)

                    \(x\) = 2 : \(\dfrac{2025}{2023}\)

                    \(x\) = \(\dfrac{4046}{2025}\)