các bạn giúp mình nha ! xin cảm ơn!
(2x-3)2-(x-5)(4x2-1)=7x+6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c) \(\dfrac{x-2}{x-1}+\dfrac{6}{x^2-x}\)
\(=\dfrac{x\left(x-2\right)}{x\left(x-1\right)}+\dfrac{6}{x\left(x-1\right)}\)
\(=\dfrac{x^2-2x+6}{x\left(x-1\right)}\)
\(=\dfrac{x^2-2x+6}{x^2-x}\)
d) \(\dfrac{x+1}{x^2-4}-\dfrac{1}{x^2+2x}\)
\(=\dfrac{x+1}{\left(x+2\right)\left(x-2\right)}-\dfrac{1}{x\left(x+2\right)}\)
\(=\dfrac{x\left(x+1\right)}{x\left(x+2\right)\left(x-2\right)}-\dfrac{x-2}{x\left(x+2\right)\left(x-2\right)}\)
\(=\dfrac{x^2+x-x+2}{x\left(x+2\right)\left(x-2\right)}\)
\(=\dfrac{x^2+2}{x\left(x^2-4\right)}\)
\(=\dfrac{x^2+2}{x^3-4x}\)

9\(x^2\) - 4 = (2\(x\) - 1).(2 - 3\(x\))
9\(x^2\) - 4 = 4\(x\) - 6\(x^2\) - 2 + 3\(x\)
9\(x^2\) - 4 - 4\(x\) + 6\(x^2\) + 2 - 3\(x\) = 0
(9\(x^2\) + 6\(x^2\)) - (4\(x\) + 3\(x\)) - (4 - 2) = 0
15\(x^2\) - 7\(x\) - 2 = 0
15\(x^2\) - 10\(x\) + 3\(x\) - 2 = 0
5\(x\)(3\(x\) - 2) + (3\(x\) - 2) = 0
(3\(x\) - 2)(5\(x\) + 1) = 0
\(\left[{}\begin{matrix}3x-2=0\\5x+1=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{1}{5}\end{matrix}\right.\)
Vậy\(x\) \(\in\) {- \(\dfrac{1}{5}\); \(\dfrac{2}{3}\)}
\(9x^2-4=\left(2x-1\right)\left(2-3x\right)\\ \Leftrightarrow\left(3x-2\right)\left(3x+2\right)=\left(2x-1\right)\left(2-3x\right)\\ \Leftrightarrow\left(3x-2\right)\left(3x+2\right)-\left(2x-1\right)\left(2-3x\right)=0\\ \Leftrightarrow\left(3x-2\right)\left(3x+2\right)+\left(2x-1\right)\left(3x-2\right)=0\\ \Leftrightarrow\left(3x-2\right)\left(3x+2+2x-1\right)=0\\ \Leftrightarrow\left(3x-2\right)\left(5x+1\right)=0\\ \Rightarrow\left[{}\begin{matrix}3x-2=0\\5x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{1}{5}\end{matrix}\right.\)

B = \(\dfrac{x^2+x-5x-5}{x^2-10x+25}\) (đk: \(x\ne5\))
B = \(\dfrac{x\left(x+1\right)-5\left(x+1\right)}{\left(x-5\right)^2}\)
B = \(\dfrac{\left(x+1\right).\left(x-5\right)}{\left(x-5\right)^2}\)
B = \(\dfrac{x+1}{x-5}\)

a:
ĐKXĐ: \(x\ne0;y\ne0\)
Đặt \(\dfrac{1}{x}=a;\dfrac{1}{y}=b\)
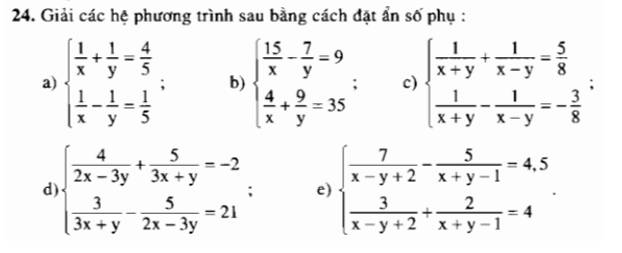
Hệ phương trình sẽ trở thành \(\left\{{}\begin{matrix}a+b=\dfrac{4}{5}\\a-b=\dfrac{1}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a=1\\a-b=\dfrac{1}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=a-\dfrac{1}{5}=\dfrac{1}{2}-\dfrac{1}{5}=\dfrac{3}{10}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{2}\\\dfrac{1}{y}=\dfrac{3}{10}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{10}{3}\end{matrix}\right.\left(nhận\right)\)
b: ĐKXĐ: \(x\ne0;y\ne0\)
Đặt \(\dfrac{1}{x}=a;\dfrac{1}{y}=b\)
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}15a-7b=9\\4a+9b=35\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}60a-28b=36\\60a+135b=140\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-163b=-104\\4a+9b=35\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{104}{163}\\a=\dfrac{4769}{652}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{4769}{652}\\\dfrac{1}{y}=\dfrac{104}{163}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{652}{4769}\\y=\dfrac{163}{104}\end{matrix}\right.\)(nhận)
c: ĐKXĐ: \(x\ne\pm y\)
Đặt \(\dfrac{1}{x+y}=a;\dfrac{1}{x-y}=b\)
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}a+b=\dfrac{5}{8}\\a-b=-\dfrac{3}{8}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a=\dfrac{5}{8}-\dfrac{3}{8}=\dfrac{2}{8}=\dfrac{1}{4}\\a+b=\dfrac{5}{8}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=\dfrac{1}{4}\\b=\dfrac{5}{8}-\dfrac{1}{4}=\dfrac{3}{8}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{x+y}=\dfrac{1}{4}\\\dfrac{1}{x-y}=\dfrac{3}{8}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=4\\x-y=\dfrac{8}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=4+\dfrac{8}{3}=\dfrac{20}{3}\\x+y=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{10}{3}\\y=4-x=4-\dfrac{10}{3}=\dfrac{2}{3}\end{matrix}\right.\left(nhận\right)\)
d: ĐKXĐ: \(y\ne-3x;y\ne\dfrac{2}{3}x\)
Đặt \(\dfrac{1}{2x-3y}=a;\dfrac{1}{3x+y}=b\)
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}4a+5b=-2\\-5a+3b=21\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}20a+25b=-10\\-20a+12b=84\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}37b=84-10=74\\4a+5b=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=2\\a=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{2x-3y}=-3\\\dfrac{1}{3x+y}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-3y=-\dfrac{1}{3}\\3x+y=\dfrac{1}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-3y=-\dfrac{1}{3}\\9x+3y=\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11x=-\dfrac{1}{3}+\dfrac{3}{2}=\dfrac{7}{6}\\y=\dfrac{1}{2}-3x\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{7}{66}\\y=\dfrac{1}{2}-3\cdot\dfrac{7}{66}=\dfrac{1}{2}-\dfrac{7}{22}=\dfrac{4}{22}=\dfrac{2}{11}\end{matrix}\right.\)
e: ĐKXĐ:\(x\ne y-2;x\ne-y+1\)
Đặt x-y+2=a; x+y-1=b
Hệ phương trình sẽ trở thành:
\(\left\{{}\begin{matrix}\dfrac{7}{a}-\dfrac{5}{b}=4,5\\\dfrac{3}{a}+\dfrac{2}{b}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{14}{a}-\dfrac{10}{b}=9\\\dfrac{15}{a}+\dfrac{10}{b}=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{29}{a}=29\\\dfrac{3}{a}+\dfrac{2}{b}=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=1\\\dfrac{2}{b}=4-\dfrac{3}{a}=4-3=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-y+2=1\\x+y-1=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y=-1\\x+y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)(nhận)

Nếu chia 15 dư 6 thì chắc chắn sẽ chia hết cho 3
Nếu chia 9 dư 1 thì chắc chắn sẽ không bao giờ chia hết cho 3
Do đó, hai điều này đối nghịch nhau
Từ đó suy ra, không có số tự nhiên nào chia 15 dư 6 và chia 9 dư 1
Giả sử tồn tại một số a chia cho 15 dư 6 và chia 9 dư 1 khi đó ta có:
\(\left\{{}\begin{matrix}a=15k+6\left(k\in N\right)\\15k+6-1⋮9\end{matrix}\right.\) ⇒ 15k + 6 - 1 ⋮ 3 ⇒ 15k + 5 ⋮ 3 ⇒ 3.(5k + 1) + 2 ⋮ 3
⇒ 2 ⋮ 3 (vô lí) Điều giả sử là sai.
Vậy không có số tự nhiên nào mà chia cho 15 dư 6 và chia 9 dư 1

a: Xét ΔABC có BM là phân giác
nên \(\dfrac{AM}{MC}=\dfrac{BA}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\)
=>\(\dfrac{AM}{3}=\dfrac{MC}{5}\)
mà AM+MC=AC=6cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AM}{3}=\dfrac{MC}{5}=\dfrac{AM+MC}{3+5}=\dfrac{6}{8}=\dfrac{3}{4}\)
=>\(AM=3\cdot\dfrac{3}{4}=\dfrac{9}{4}\left(cm\right)\)
b: Xét ΔEBC có GQ//BC
nên \(\dfrac{EG}{EB}=\dfrac{EQ}{EC}\)
Xét ΔMBC có QI//BC
nên \(\dfrac{CI}{CM}=\dfrac{BQ}{BM}\)
Ta có: \(\widehat{ABM}=\widehat{MBC}=\dfrac{\widehat{ABC}}{2}\)
\(\widehat{ACE}=\widehat{ECB}=\dfrac{\widehat{ACB}}{2}\)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABM}=\widehat{ACE}=\widehat{MBC}=\widehat{ECB}\)
Xét ΔQBC có \(\widehat{QBC}=\widehat{QCB}\)
nên ΔQBC cân tại Q
=>QB=QC
Xét ΔAMB và ΔAEC có
\(\widehat{ABM}=\widehat{ACE}\)
AB=AC
\(\widehat{BAM}\) chung
Do đó: ΔAMB=ΔAEC
=>MB=EC
mà MB=MQ+QB
và EC=EQ+QC
và QB=QC
nên MQ=EQ
\(\dfrac{EG}{EB}+\dfrac{CI}{CM}=\dfrac{EQ}{EC}+\dfrac{BQ}{BM}=1-\dfrac{CQ}{CE}+\dfrac{BQ}{BM}\)
\(=1-\dfrac{BQ}{BM}+\dfrac{BQ}{BM}=1\)

\((z-3)^2-(x-2y)^2\\=[(z-3)-(x-2y)][(z-3)+(x-2y)]\\=(z-3-x+2y)(z-3+x-2y)\)
\(\left(z-3\right)^2-\left(x-2y\right)^2\)
\(=\left[\left(z-3\right)-\left(x-2y\right)\right]\left[\left(z-3\right)+\left(x-2y\right)\right]\)
\(=\left(z-3-x+2y\right)\left(z-3+x-2y\right)\)

\(\frac{x-1}{1999}+\frac{x-2}{1998}=\frac{x-3}{1997}+\frac{x-4}{1996}\\\Leftrightarrow \left(\frac{x-1}{1999}-1\right) +\left(\frac{x-2}{1998}-1\right)=\left(\frac{x-3}{1997}-1\right)+\left(\frac{x-4}{1996}-1\right)\\\Leftrightarrow \frac{x-2000}{1999}+\frac{x-2000}{1998}=\frac{x-2000}{1997}+\frac{x-2000}{1996}\\\Leftrightarrow \frac{x-2000}{1999}+\frac{x-2000}{1998}-\frac{x-2000}{1997}-\frac{x-2000}{1996}=0\\ \Leftrightarrow (x-2000)\left(\frac{1}{1999}+\frac{1}{1998}-\frac{1}{1997}-\frac{1}{1996}\right)=0\\\Leftrightarrow x-2000=0\left(\text{vì } \frac{1}{1999}+\frac{1}{1998}-\frac{1}{1997}-\frac{1}{1996}\ne0\right)\\\Leftrightarrow x=2000\)
Vậy phương trình đã cho có 1 nghiệm duy nhất là \(x=2000\).

ĐỐI VỚI BÀI TOÁN LẬP PHƯƠNG TRÌNH VỀ QUÃNG ĐƯỜNG VẬN TỐC THỜI GIAN THÌ NÊN LẬP BẢNG ĐỂ GIẢI DỄ DÀNG HƠN
| vận tốc | quãng đường | thời gian | |
| A - B | x + 10 | 4(x + 10) | 4 |
| B - A | x - 10 | 5(x - 10) | 5 |
vì vận tốc của dòng nước là 10km/h nên:
vận tốc cano đi từ A đến B là: x + 10 (km/h)
vận tốc cano đi từ B đến A là: x - 10 (km/h)
quãng đường cano đi từ A đến B là: 4(x + 10) (km)
quãng đường cano đu từ B đến A là: 5(x - 10) (km)
theo đề ta có phương trình:
4(x + 10) = 5(x - 10)
4x + 40 = 5x - 50
4x - 5x = -40 - 50
-x = -90
x = 90
quãng đường AB dài là: 4(90+10) = 400 (km)
VẬY QUÃNG ĐƯỜNG AB DÀI 400KM
Cùng quãng sông nên vận tốc và thời gian tỉ lệ nghịch
Tỉ số thời gian đi xuôi so với đi ngược là : \(\dfrac{4}{5}\)
=> Tỉ số vận đi xuôi so với đi ngược là : \(\dfrac{5}{4}\)
Ta có sơ đồ:
Vận tốc đi xuôi :|------|------|------|------|------|
Vận tốc đi ngược :|------|------|------|------|
Hiệu vận tốc đi xuôi với đi ngược là:
10 x 2 = 20 (km/giờ)
=> Vận tốc đi xuôi dòng của ca nô là:
20 : (5 - 4) x 5 = 100 (km/giờ)
=> Khoảng cách từ A đến B là:
100 x 4 = 400 (km)
Đ/s: 400 km
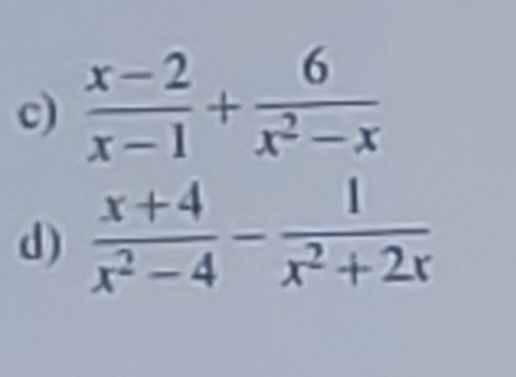
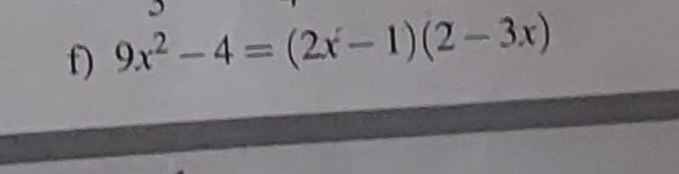
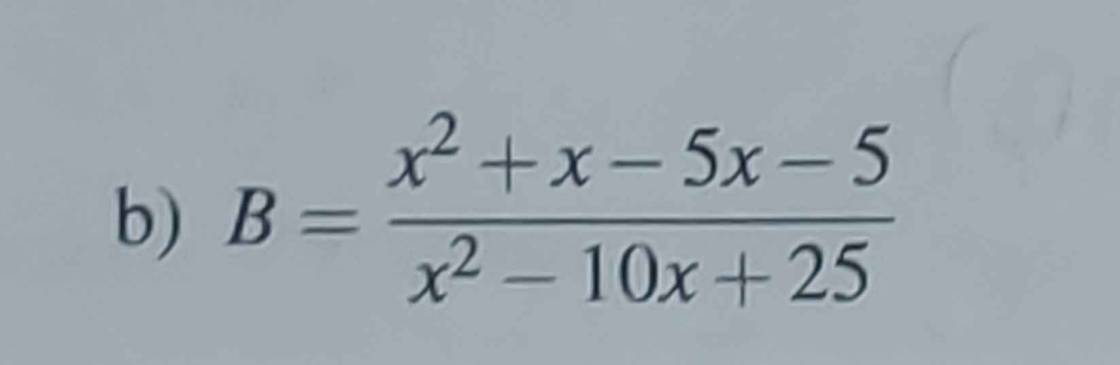


\(\left(2x-3\right)^2-\left(x-5\right)\left(4x^2-1\right)=7x+6\)
=>\(4x^2-12x+9-\left(4x^3-x-20x^2+5\right)=7x+6\)
=>\(4x^2-12x+9-4x^3+20x^2+x-5-7x-6=0\)
=>\(-4x^3+24x^2-18x-2=0\)
=>\(-4x^3+4x^2+20x^2-20x+2x-2=0\)
=>\(-4x^2\left(x-1\right)+20x\left(x-1\right)+2\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(-4x^2+20x+2\right)=0\)
=>\(\left[{}\begin{matrix}x-1=0\\-4x^2+20x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{5\pm3\sqrt{3}}{2}\end{matrix}\right.\)
mong các bạn giúp đỡ
ngày 12/6 là mình đi học rồi vào buổi sáng