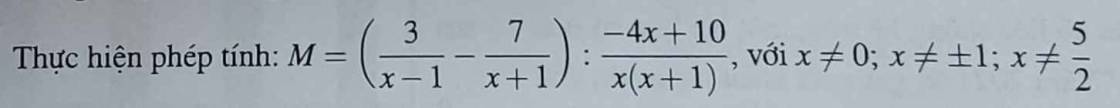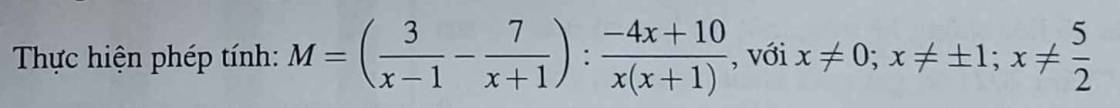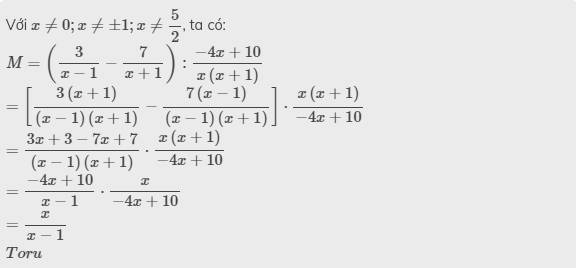x²y + xy² - x - y

= (x²y + xy²) - (x + y)

= xy(x + y) - (x + y)

= (x + y)(xy - 1)

a) Ta tính tổng số các cặp lớp phân biệt có thể xảy ra.

 Vị trí đầu tiên có \(x\) cách chọn và vị trí thứ hai sẽ có \(x-1\) cách chọn (do một lớp bất kì không thể đấu với chính lớp đó). Nhưng nếu tính như trên, thì mỗi trận đấu giữa 2 đội bất kì sẽ bị lặp lại thêm 1 lần, nên tổng số trận đấu khác nhau là \(\dfrac{x\left(x-1\right)}{2}\)

 b) Cho \(\dfrac{x\left(x-1\right)}{2}=105\)

\(\Leftrightarrow x^2-x-210=0\)

\(\Leftrightarrow\left(x-21\right)\left(x+20\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=21\left(nhận\right)\\x=-20\left(loại\right)\end{matrix}\right.\)

Vậy có 21 đội tham gia.

Với \(x\ne0;x\ne\pm1;x\ne\dfrac{5}{2}\), ta có:

\(M=\left(\dfrac{3}{x-1}-\dfrac{7}{x+1}\right):\dfrac{-4x+10}{x\left(x+1\right)}\)

\(=\left[\dfrac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}-\dfrac{7\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\right]\cdot\dfrac{x\left(x+1\right)}{-4x+10}\)

\(=\dfrac{3x+3-7x+7}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x\left(x+1\right)}{-4x+10}\)

\(=\dfrac{-4x+10}{x-1}\cdot\dfrac{x}{-4x+10}\)

\(=\dfrac{x}{x-1}\)

\(Toru\)

Bạn nên gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn.

a) ĐKXĐ: x\(\ne\)0, x\(\ne\)2 

Ta có: 
 A= 2x-4/ x²- 2x = 2(x-2)/ x(x-2) = 2/x

Vậy...

b) Ta thấy x=26 thỏa mãn ĐKXĐ

Thay x=26 vào bt A ta được
   A= 2/26 = 1/13

Vậy....

c) Với x\(\ne\)0, x\(\ne\)2 ta có A=12 \(\Leftrightarrow\) 2/x =12 \(\Leftrightarrow\) x=1/6

Vậy....

   \(x^2\) - 8\(x\) + 19

= (\(x^2\) -2.\(x\) . 4 + 4²) + 3

= (\(x\) - 4)² + 3  

Vì (\(x\) - 4)² ≥ 0 ∀ \(x\) ⇒ (\(x\) - 4)² + 3 ≥ 3 dấu bằng xảy ra khi  

\(x\) - 4 = 0 ⇒ \(x\) = 4

Vậy giá trị nhỏ nhất của  \(x^2\) - 8\(x\) + 19 là 3 xảy ra .khi \(x\) = 4

Q = x^2 + 8x + 20

= (x^2 + 8x + 16) + 4

= (x+4)^2 + 4 ≥ 4 với mọi x

Dấu = xảy ra khi :

x+4=0 hay x = -4

VẬY MIN Q = 4 tại x = -4

Q = x²+ 8x + 20 

    = x²+ 2.4.x + 16+ 4

    = (x+4)²+4

Vì (x+4)² \(\ge\) 0 với mọi x \(\Rightarrow\) (x+4)²+ 4\(\ge\) 0+4 

                                        hay Q\(\ge\) 4

Dấu "=" xảy ra \(\Leftrightarrow\) (x+4)²=0 \(\Leftrightarrow\) x+4=0 \(\Leftrightarrow\) x= -4

 Vậy Q đạt giá trị nhỏ nhất khi x= -4

\(x^2-y^2+2x+1\\=(x^2+2x+1)-y^2\\=(x+1)^2-y^2\\=(x+1-y)(x+1+y)\)