(14:X:6)x7=84
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
\(x^2+y^2=2\)
\(\Rightarrow0\le x\le\sqrt{2}\)
\(0\le y\le\sqrt{2}\)(1)
Lại có:
\(P=x+3y\)
\(\Rightarrow3y\ge0\) (1)
Để P nhỏ nhất thì x hoặc 3y đạt giá trị nhỏ nhất vì x và 3y đều lớn hơn 0.
Xét trường hợp x nhỏ nhất:
\(x\ge0\) dấu bằng xảy ra \(\Leftrightarrow x=0\Rightarrow y=\sqrt{2}\)
\(\Rightarrow P=3\sqrt{2}\)
Xét trường hợp y nhỏ nhất.
\(y\ge0\) dấu bằng xảy ra \(\Leftrightarrow y=0\Rightarrow x=\sqrt{2}\)
\(\Rightarrow P=\sqrt{2}\)
Vậy giá trị nhỏ nhất của P tại \(\left(x,y\right)=\left(\sqrt{2},0\right)\)

\(\dfrac{1}{2}\) số nước trong bể nặng số kg là
88 - 66 =22 (kg)
Bể 0 nặng số kg là
88 - 22 x 2 =44 kg

2:
a: Khi m=-1 thì (d): \(y=2x+\left(-1\right)+1=2x\)
Phương trình hoành độ giao điểm là:
\(x^2=2x\)
=>\(x^2-2x=0\)
=>(x-2)*x=0
=>\(\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Khi x=0 thì \(y=0^2=0\)
Khi x=2 thì \(y=2^2=4\)
Vậy: (P) giao (d) tại A(0;0); B(2;4)
b: Phương trình hoành độ giao điểm là:
\(x^2=2x+m+1\)
=>\(x^2-2x-m-1=0\)
\(\Delta=\left(-2\right)^2-4\cdot1\left(-m-1\right)\)
\(=4+4m+4=4m+8\)
Để (P) cắt (d) tại hai điểm phân biệt thì \(\Delta>0\)
=>4m+8>0
=>m>-2
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2\\x_1x_2=\dfrac{c}{a}=-m-1\end{matrix}\right.\)
Đặt \(A=\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{x_1+x_2}{x_1x_2}=\dfrac{2}{-m-1}=\dfrac{-2}{m+1}\)
Để A là số nguyên thì \(-2⋮m+1\)
=>\(m+1\in\left\{1;-1;2;-2\right\}\)
=>\(m\in\left\{0;-2;1;-3\right\}\)
mà m>-2
nên \(m\in\left\{0;1\right\}\)

\(S_{HCN}=a\times b\) với a,b là chiều dài và chiều rộng hình chữ nhật cùng đơn vị độ dài.

\(x=\sqrt[3]{a^3+a+\dfrac{1}{3}\sqrt{27a^4+6a^2+\dfrac{1}{3}}}+\sqrt[3]{a^3+a-\dfrac{1}{3}\sqrt{27a^4+6a^2+\dfrac{1}{3}}}\)
\(=\sqrt[3]{a^3+a+\dfrac{1}{3}\cdot\sqrt{\left(3\sqrt{3}a^2\right)^2+2\cdot3\sqrt{3}\cdot a^2\cdot\dfrac{1}{\sqrt{3}}+\left(\dfrac{1}{\sqrt{3}}\right)^2}}+\sqrt[3]{a^3+a-\dfrac{1}{3}\cdot\sqrt{\left(3\sqrt{3}a^2\right)^2+2\cdot3\sqrt{3}\cdot a^2\cdot\dfrac{1}{\sqrt{3}}+\left(\dfrac{1}{\sqrt{3}}\right)^2}}\)
\(=\sqrt[3]{a^3+a+\dfrac{1}{3}\sqrt{\left(3\sqrt{3}a^2+\dfrac{1}{\sqrt{3}}\right)^2}}+\sqrt[3]{a^3+a-\dfrac{1}{3}\sqrt{\left(3\sqrt{3}a^2+\dfrac{1}{\sqrt{3}}\right)^2}}\)
\(=\sqrt[3]{a^3+a+\dfrac{1}{3}\left(3\sqrt{3}a^2+\dfrac{1}{\sqrt{3}}\right)}+\sqrt[3]{a^3+a-\dfrac{1}{3}\left(3\sqrt{3}a^2+\dfrac{1}{\sqrt{3}}\right)}\)
\(=\sqrt[3]{a^3+a+\sqrt{3}a^2+\dfrac{1}{3\sqrt{3}}}+\sqrt[3]{a^3+a-\sqrt{3}a^2-\dfrac{1}{3\sqrt{3}}}\)
\(=\sqrt[3]{a^3+3\cdot a^2\cdot\dfrac{1}{\sqrt{3}}+3\cdot a\cdot\dfrac{1}{3}+\left(\dfrac{1}{\sqrt{3}}\right)^3}+\sqrt[3]{a^3-3\cdot a^2\cdot\dfrac{1}{\sqrt{3}}+3\cdot a\cdot\dfrac{1}{3}-\left(\dfrac{1}{\sqrt{3}}\right)^3}\)
\(=\sqrt[3]{\left(a+\dfrac{1}{\sqrt{3}}\right)^3}+\sqrt[3]{\left(a-\dfrac{1}{\sqrt{3}}\right)^3}\)
\(=a+\dfrac{1}{\sqrt{3}}+a-\dfrac{1}{\sqrt{3}}=2a\)

Giải:
Sau khi bán đi \(\dfrac{3}{7}\) số trứng thì số trứng còn ứng với phân số là:
1 - \(\dfrac{3}{7}\) = \(\dfrac{4}{7}\) (số trứng)
\(\dfrac{4}{7}\) số trứng ứng với:
30 + 18 = 48 (quả)
Ban đầu người đó có số trứng là:
48 : \(\dfrac{4}{7}\) = 84 (quả)
Đáp số: 84 quả.

Ta có: SAEC = SABC ( Vì chung đường cao hạ từ A xuống đáy và đấy EC = đáy CB)
=> SAEC là: 5cm2
SAEB là : 5+ 5 = 10 cm2
SAEB = SEBD ( Vì chung đường cao và đáy AB = đáy BD)
Vậy SEBD là 10 cm2
SADE là : 10 + 10 = 20 ( cm2)
Đáp số: 20cm2

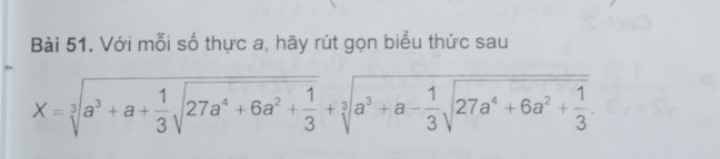
(14 : \(x\) : 6) x 7 = 84
14 : \(x\) : 6 = 84 : 7
14 : \(x\) : 6 = 12
14 : \(x\) = 12 x 6
\(x\) = 72
\(x\) = 14 : 72
\(x\) = \(\dfrac{7}{36}\)
(14 : x : 6) × 7 = 84
14 : x : 6 = 84 : 7
14 : x : 6 = 12
14 : x = 12 × 6
14 : x = 72
x = 14 : 72
x = 7/36