Lời giải:

Với $n$ nguyên, để $\frac{3n-1}{n-1}$ (điều kiện: $n\neq 1$) nguyên thì:

$3n-1\vdots n-1$

$\Rightarrow 3(n-1)+2\vdots n-1$

$\Rightarrow 2\vdots n-1$

$\Rightarrow n-1\in \left\{\pm 1; \pm 2\right\}$

$\Rightarrow n\in \left\{2; 0; 3; -1\right\}$ (thỏa mãn)

A<B vì các số mũ đều giống nhau nên sẽ s2 phần số nguyên vậy nên nếu s2 5 với 6 thì 5 bé hơn nên A<B

giải chi tiết 

Bài 3.31 

Cho A = \(\dfrac{5n+6}{8n+7}\) (n \(\in\) N)

Gọi ƯCLN(5n + 6; 8n + 7) = d

Ta có: \(\left\{{}\begin{matrix}5n+6⋮d\\8n+7⋮d\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}8.\left(5n+6\right)⋮d\\5.\left(8n+7\right)⋮d\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}40n+42⋮d\\40n+35⋮d\end{matrix}\right.\)

40n + 42 - (40n + 35) ⋮ d

40n + 42 - 40n - 35 ⋮ d

(40n - 40n) + (42 - 35) ⋮ d

                              7 ⋮ d ⇒ d \(\in\) Ư(7) = {1; 7} ⇒ d \(\in\) {1; 7}

Nếu d = 7 ta có: 8n + 7 ⋮ 7 ⇒ 8n ⋮ 7 ⇒ n ⋮ 7

Mặt khác ta có: 5n + 6 ⋮ 7 ⇒ 6 ⋮ 7 (vô lí)

Vậy d = 7 loại

Hay phân số A = \(\dfrac{5n+6}{8n+7}\) không thể rút gọn cho số nào cả.

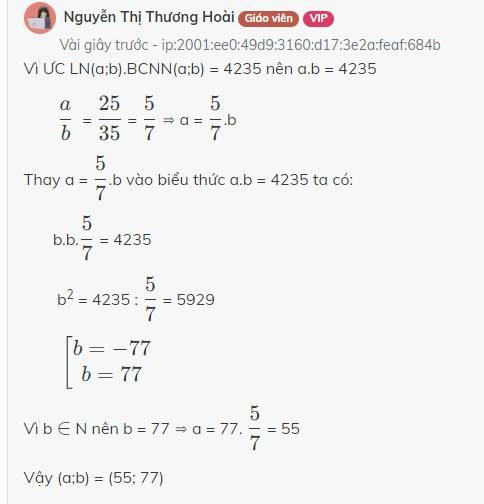
Vì ƯC LN(a;b).BCNN(a;b) = 4235 nên a.b = 4235

        \(\dfrac{a}{b}\)  = \(\dfrac{25}{35}\) = \(\dfrac{5}{7}\) ⇒ a = \(\dfrac{5}{7}\).b

Thay a = \(\dfrac{5}{7}\).b vào biểu thức a.b = 4235 ta có:

       b.b.\(\dfrac{5}{7}\) = 4235

        b² = 4235 : \(\dfrac{5}{7}\) = 5929 

         \(\left[{}\begin{matrix}b=-77\\b=77\end{matrix}\right.\)

Vì b \(\in\) N nên b = 77 ⇒ a = 77. \(\dfrac{5}{7}\) = 55

Vậy (a;b) = (55; 77)

Số trái táo và lê so với cả rổ:

1 - 1/3 = 2/3

Số quả táo so với cả rổ:

5/6 × 2/3 = 5/9

Số trái lê so với cả rổ:

2/3 - 5/9 = 1/9

Số trái cây trong rổ:

20 : 1/9 = 180 (trái)

rổ thứ 1 ít hơn rổ thứ 2 120 quả táo và bằng 1 phần 3 rổ thứ 2.Hỏi mỗi rổ đựng được bao nhiêu quả táo ?

Đặt A = y⁰.y⁵.y¹⁰...y¹⁹⁹⁵

= y⁵.y¹⁰...y¹⁹⁹⁵

= y⁵⁺¹⁰⁺···⁺¹⁹⁹⁵

Số số hạng của mũ:

(1995 - 5) : 5 + 1 = 399 (số)

Tổng mũ là:

(1995 + 5) . 399 : 2 = 39900

⇒ A = y³⁹⁹⁰⁰

1h10ph = 1\(\dfrac{1}{6}\)h

1 giờ = 60 phút.

⇒ 10 phút = \(\dfrac{10}{60}=\dfrac{1}{6}\) giờ.

Vậy ta có \(1h10ph=1\dfrac{1}{6}\) giờ

chụi

ta có :

A=17^11-1/17^12-1

  =17^10.17-1/17^11.17-1

B=17^10+1/17^11+1

ta thấy 17^11>17^10

mà 1/17^12<1/17^11

lại có 17>1/17

nên=>A>B