
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)
\(3x\left(x-4\right)+7\left(x-4\right)=0\\ \Leftrightarrow\left(x-4\right)\left(3x+7\right)\\ \Leftrightarrow\left[{}\begin{matrix}x-4=0\\3x+7=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=4\\3x=-7\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=4\\x=-\dfrac{7}{3}\end{matrix}\right.\)
Vậy: ...
b)
\(\left(4x^2-9\right)+\left(x+2\right)\left(3-2x\right)=0\\ \Leftrightarrow\left(2x-3\right)\left(2x+3\right)-\left(x+2\right)\left(2x-3\right)=0\\ \Leftrightarrow\left(2x-3\right)\left(2x+3-x-2\right)=0\\ \Leftrightarrow\left(2x-3\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-1\end{matrix}\right.\)
Vậy: ...
c)
\(\left(x-1\right)^2=\left(2x+3\right)^2\\ \Leftrightarrow\left(x-1\right)^2-\left(2x+3\right)^2=0\\ \Leftrightarrow\left(x-1+2x+3\right)\left(x-1-2x-3\right)=0\\ \Leftrightarrow\left(3x+2\right)\left(-x-4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}3x=-2\\-x=4\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{2}{3}\\x=-4\end{matrix}\right.\)
Vậy: ...
d)
\(x^2-6x+5=0\\ \Leftrightarrow x^2-5x-x+5=0\\ \Leftrightarrow x\left(x-5\right)-\left(x-5\right)=0\\ \Leftrightarrow\left(x-5\right)\left(x-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=5\\x=1\end{matrix}\right.\)
Vậy: ...

a)
\(\left(x-5\right)\left(3x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-5=0\\3x+4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=5\\3x=-4\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=5\\x=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy: ...
b)
\(\left(\dfrac{2}{3}x-1\right)\left(\dfrac{1}{3}x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}\dfrac{2}{3}x-1=0\\\dfrac{1}{3}x+2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}\dfrac{2}{3}x=1\\\dfrac{1}{3}x=-2\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1:\dfrac{2}{3}\\x=-2:\dfrac{1}{3}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-6\end{matrix}\right.\)
Vậy: ...
c)
\(\left(x+7\right)\left(\dfrac{x}{3}-\dfrac{2-x}{6}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+7=0\\\dfrac{x}{3}-\dfrac{2-x}{6}=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-7\\\dfrac{2x}{6}-\dfrac{2-x}{6}=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-7\\\dfrac{2x-2+x}{6}=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-7\\3x-2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-7\\3x=2\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-7\\x=\dfrac{2}{3}\end{matrix}\right.\)
Vậy: ...

a) y = 2x - 1 (a = 2; b=-1) và y = -x + 1 (a'=-1;b'=1)
Có a ≠ a' nên y = 2x - 1 và y = -x +1 cắt nhau nên hệ pt có 1 nghiệm duy nhất
b) 3x + 2y = 5 ⇔ \(y=\dfrac{5-3x}{2}=\dfrac{-3}{2}x+\dfrac{5}{2}\) (`a=-3/2;b=5/2`)
\(x-2y=2\Leftrightarrow y=\dfrac{2-x}{-2}\Leftrightarrow y=\dfrac{1}{2}x-1\left(a'=\dfrac{1}{2};b'=-1\right)\)
Có a ≠ a' nên hpt có 1 nghiệm duy nhất
c) \(x+y=2\Leftrightarrow y=-x+2\left(a=-1;b=2\right)\)
\(3x+3y=6\Leftrightarrow3\left(x+y\right)=6\Leftrightarrow x+y=2\Leftrightarrow y=-x+2\left(a'=-1;b=2\right)\)
Có a=a' và b=b' nên hpt có vô sô nghiệm

\(\left\{{}\begin{matrix}mx+y=3\\4x+my=6\end{matrix}\right.\) (1)
Để hpt có nghiệm thì: \(\dfrac{m}{4}\ne\dfrac{1}{m}\Leftrightarrow m\ne\pm2\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2x+my=3m\\4x+my=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(m^2-4\right)x=3m-6\\mx+y=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3m-6}{m^2-4}=\dfrac{3}{m+2}\\\dfrac{3m}{m+2}+y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{m+2}\\y=3-\dfrac{3m}{m+2}=\dfrac{6}{m+2}\end{matrix}\right.\)
Mà: \(\left\{{}\begin{matrix}x_o>2\\y_o>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{m+2}>2\\\dfrac{6}{m+2}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2< m< -\dfrac{1}{2}\\m>-2\end{matrix}\right.\Leftrightarrow-2< m< -\dfrac{1}{2}\)

Gọi T là giao điểm của EF và BC. Gọi J là trung điểm DT. Khi đó vì \(\widehat{TKD}=90^o\) nên \(K\in\left(J,JD\right)\). Đặt \(JB=b,JC=c,JD=JT=d\).
Dễ thấy \(AE=AF,BF=BD,CD=CE\) nên \(\dfrac{FA}{FB}.\dfrac{DB}{DC}.\dfrac{EC}{EA}=1\)
Hơn nữa, áp dụng định lý Menelaus cho tam giác ABC với cát tuyến EFT, ta có: \(\dfrac{FA}{FB}.\dfrac{TB}{TC}.\dfrac{EC}{EA}=1\)
Từ đó suy ra \(\dfrac{DB}{DC}=\dfrac{TB}{TC}\)
\(\Leftrightarrow\dfrac{JD-JB}{JC-JD}=\dfrac{JB+JT}{JC+JT}\)
\(\Leftrightarrow\dfrac{d-b}{c-d}=\dfrac{b+d}{c+d}\)
\(\Leftrightarrow\left(d-b\right)\left(c+d\right)=\left(c-d\right)\left(b+d\right)\)
\(\Leftrightarrow cd+d^2-bc-bd=bc+cd-bd-d^2\)
\(\Leftrightarrow2d^2=2bc\)
\(\Leftrightarrow JD^2=JB.JC=JK^2\) \(\left(vìJD=JK\right)\)
\(\Leftrightarrow\dfrac{JK}{JC}=\dfrac{JB}{JK}\)
Xét tam giác JBK và JKC, có:
\(\dfrac{JK}{JC}=\dfrac{JB}{JK}\) và \(\widehat{J}\) chung nên
\(\Delta JBK\sim\Delta JKC\left(c.g.c\right)\)
\(\Rightarrow\dfrac{KB}{KC}=\dfrac{JB}{JK}=\dfrac{JB}{JD}=\dfrac{b}{d}\)
Lại có \(d^2=bc\)
\(\Leftrightarrow d^2-bd=bc-bd\)
\(\Leftrightarrow d\left(d-b\right)=b\left(c-d\right)\)
\(\Leftrightarrow\dfrac{b}{d}=\dfrac{d-b}{c-d}\)
Như vậy \(\dfrac{KB}{KC}=\dfrac{b}{d}=\dfrac{d-b}{c-d}=\dfrac{JD-JB}{JC-JD}=\dfrac{DB}{DC}\)
Do đó theo tính chất đường phân giác trong tam giác, KD là phân giác \(\widehat{BKC}\) (đpcm)

Gọi chữ số hàng chục là: \(a\left(a\inℕ^∗,a\le9\right)\)
Theo đề, suy ra chữ số hàng đơn vị là: \(10-a\)
Số phải tìm có dạng: \(\overline{a\left(10-a\right)}\)
Nếu đổi chỗ, ta được số: \(\overline{\left(10-a\right)a}\)
Mà: Nếu đổi chỗ hai chữ số ấy ta được số mới hơn số cũ 18
Nên ta có pt:
\(\overline{\left(10-a\right)a}-\overline{a\left(10-a\right)}=18\\ \Leftrightarrow\overline{\left(10-a\right)0}+a-\left(\overline{a0}+10-a\right)=18\\ \Leftrightarrow10\left(10-a\right)+a-10a-10+a=18\\ \Leftrightarrow100-10a+a-10a-10+a-18=0\\ \Leftrightarrow-18a+72=0\\ \Leftrightarrow-18a=-72\\ \Leftrightarrow a=4\left(TMDK\right)\)
Vậy SPT là: 46
tổng của 2 số đó là 10 nên ta có: a + b = 10
nếu đổi chỗ thì số mới hơn số cũ là: \(\overline{ba}=\overline{ab}+18\)
\(\overline{ab}=10a+b;\overline{ba}=10b+a \)
ta có: 10b + a = 10a + b + 18
10b + a - 10a - b = 18
9b - 9a = 18
b - a = 2
ta có hệ phương trình:
\(\cdot a+b=10\\ \cdot b-a=2\)
(a + b) + (b - a) = 10 + 2
a + b + b - a = 12
2b = 12
b = 6
thay b = 6 vào a + b = 10
a + 6 = 10
a = 4
vậy số cần tìm là 46
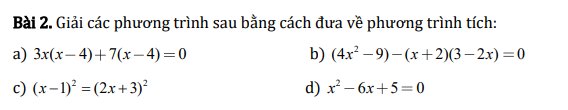
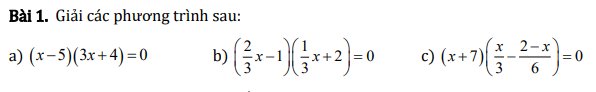



a) Đặt: `4x-5=t`
\(t^2+2t+1=0\\ \Leftrightarrow\left(t+1\right)^2=0\\ \Leftrightarrow t+1=0\\ \Leftrightarrow t=-1\)
\(\Rightarrow4x-5=-1\\ \Leftrightarrow4x=-1+5\\ \Leftrightarrow4x=4\\ \Leftrightarrow x=1\)
b) Đặt: \(x^2-x=t\)
\(t\left(t+1\right)=6\\ \Leftrightarrow t^2+t-6=0\\ \Leftrightarrow t^2-2t+3t-6=0\\ \Leftrightarrow t\left(t-2\right)+3\left(t-2\right)=0\\ \Leftrightarrow\left(t-2\right)\left(t+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}t=2\\t=-3\end{matrix}\right.\)
Với:
\(t=2\Rightarrow x^2-x=2\Leftrightarrow x^2-x-2=0\Leftrightarrow\left(x+1\right)\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
Với:
\(t=-3\Rightarrow x^2-x=-3\Leftrightarrow x^2-x+3=0\)
Mà: `x^2-x+3>0` nên vô lý