Lời giải:

$2020\equiv 1\pmod 3\Rightarrow 2020x^3\equiv x^3\pmod 3$

$2021\equiv -1\pmod 3\Rightarrow 2021x\equiv -x\pmod 3$
$\Rightarrow 2020x^3+2021x\equiv x^3-x\pmod 3$
Mà $x^3-x=x(x^2-1)=x(x-1)(x+1)$ là tích 3 số nguyên liên tiếp nên $x^3-x\equiv 0\pmod 3$

$\Rightarrow 2020x^3+2021x\equiv 0\pmod 3(*)$

Mặt khác:
$y^{2022}=(y^{1011})^2$ là scp nên $y^{2022}\equiv 0,1\pmod 3$

$2023\equiv 1\pmod 3$

$\Rightarrow y^{2022}+2023\equiv 1,2\pmod 3(**)$

Từ $(*); (**)\Rightarrow 2020x^3+2021x\neq y^{2022}+2023$ với mọi $x,y$ nguyên.

Do đó không tồn tại $x,y$ thỏa đề.

Lời giải:

$2020\equiv 1\pmod 3\Rightarrow 2020x^3\equiv x^3\pmod 3$

$2021\equiv -1\pmod 3\Rightarrow 2021x\equiv -x\pmod 3$
$\Rightarrow 2020x^3+2021x\equiv x^3-x\pmod 3$
Mà $x^3-x=x(x^2-1)=x(x-1)(x+1)$ là tích 3 số nguyên liên tiếp nên $x^3-x\equiv 0\pmod 3$

$\Rightarrow 2020x^3+2021x\equiv 0\pmod 3(*)$

Mặt khác:
$y^{2022}=(y^{1011})^2$ là scp nên $y^{2022}\equiv 0,1\pmod 3$

$2023\equiv 1\pmod 3$

$\Rightarrow y^{2022}+2023\equiv 1,2\pmod 3(**)$

Từ $(*); (**)\Rightarrow 2020x^3+2021x\neq y^{2022}+2023$ với mọi $x,y$ nguyên.

Do đó không tồn tại $x,y$ thỏa đề.

điếc = hư tai 

hư tai => hai tư = 24

Vậy đàn chuột có 24 con nhé 

cảm ơn Dang Tung đã trả lời câu hỏi! 

Nhưng đây không phải là đố vui mà.

thế nó mới khó, Dang Tung hiểu không?

Câu 5:

\(A=\dfrac{2}{x}+\dfrac{6}{y}+\dfrac{9}{3x+y}\)

\(=\dfrac{2\left(3x+y\right)}{xy}+\dfrac{9}{3x+y}\)

\(=\dfrac{3x+y}{6}+\dfrac{9}{3x+y}\left(xy=12\right)\)

\(=\dfrac{3x+y}{16}+\dfrac{9}{3x+y}+\dfrac{5\left(3x+y\right)}{48}\)

\(\ge2\sqrt{\dfrac{3x+y}{16}.\dfrac{9}{3x+y}}+\dfrac{5.2\sqrt{3x.y}}{48}\)

\(=2\sqrt{\dfrac{9}{16}}+\dfrac{10\sqrt{3.12}}{48}=\dfrac{11}{4}\)

Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=6\end{matrix}\right.\)

 Gọi 2 số nguyên tố đó là p, q và giả sử \(p>q\). Khi đó ta có \(p+q,p-q\) đều là các số nguyên tố.

 Nếu \(p-q=2\) \(\Rightarrow p+q=2\) (vì \(\left(p-q\right)+\left(p+q\right)=2p⋮2\)), vô lí

 Tương tự với TH \(p+q=2\) cũng sẽ dẫn tới điều vô lí.

 Do đó \(p+q,p-q\) lẻ, mà p và q đều các số nguyên tố \(\Rightarrow q=2\)

 Vậy, ta cần tìm p để \(p\pm2\) là các số nguyên tố \(\Rightarrow p\ge5\)

 Xét \(p=5\) thì \(p+2=7;p-2=3\) thỏa mãn.

 Xét \(p>5\) thì p có dạng \(p=6k+1,p=6k+5\left(k\ge1\right)\), khi đó dễ thấy rằng \(p+2,p-2\) là hợp số, vô lí.

 Vậy \(p=5,q=2\) là cặp số nguyên tố duy nhất thỏa mãn đề bài.

5 + 2 = 7

5 - 2 = 3

Hai số đó là 2 và 5

1963+1964+1965+1966+1967+.......+2021+2022+2023
Gọi A = 1963+1964+1965+1966+1967+.......+2021+2022+2023

 Số số hạng của S là: 

 \(\dfrac{2023-1963}{1}+1=71\left(\text{Số số hạng}\right)\) 

Tổng của A là:

\(\dfrac{\left(2023+1963\right).71}{2}=141503\)

Vậy tổng của 1963+1964+1965+1966+1967+...+2021+2022+2023+2024 = 141503

toán lớp 1 haha

Sai

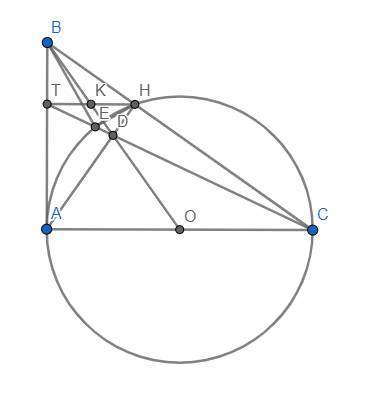
 Gọi T là giao điểm của CD và AB. Khi đó xét tứ giác ACHT, ta có:

O (trung điểm AC), D (giao điểm của 2 đường chéo) và B (giao điểm của 2 đường thẳng chứa 2 cạnh đối) thẳng hàng nên ACHT là hình thang. (bổ đề hình thang quen thuộc)

 \(\Rightarrow\) HT//AC \(\Rightarrow\) H, K, T thẳng hàng.

 Lại có \(\widehat{CEH}=\widehat{CAH}\) (góc nội tiếp cùng chắn cung AH)

 Mà \(\widehat{CAH}=\widehat{B}\) (cùng phụ với góc C)

 \(\Rightarrow\widehat{CEH}=\widehat{B}\)

 \(\Rightarrow\) Tứ giác BTEH nội tiếp \(\Rightarrow\widehat{BEH}=\widehat{BTH}\)

Mà \(\widehat{BTH}=90^o\) nên \(\widehat{BEH}=90^o\). Ta có đpcm.