Tỉ số giữa số dân của xã thứ nhất và xã thứ ba là:

\(\dfrac{1}{2}\cdot\dfrac{1}{4}=\dfrac{1}{8}\)

Số dân của xã thứ ba là: \(110000:\left(\dfrac{1}{8}+\dfrac{1}{4}+1\right)=110000:\dfrac{11}{8}=80000\left(người\right)\)

Số dân của xã thứ hai là: \(80000\cdot\dfrac{1}{4}=20000\left(người\right)\)

Số dân của xã thứ nhất là \(20000\cdot\dfrac{1}{2}=10000\left(người\right)\)

\(A=\dfrac{2023}{1\cdot2}+\dfrac{2023}{2\cdot3}+...+\dfrac{2023}{2022\cdot2023}\)

\(=2023\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{2022\cdot2023}\right)\)

\(=2023\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2022}-\dfrac{1}{2023}\right)\)

\(=2023\left(1-\dfrac{1}{2023}\right)=2023\cdot\dfrac{2022}{2023}=2022\)

\(A=\dfrac{2023}{1.2}+\dfrac{2023}{2.3}+\dfrac{2023}{3.4}+...+\dfrac{2023}{2022.2023}\)

\(A=\dfrac{2023}{1}.\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{2022.2023}\right)\)

\(A=\dfrac{2023}{1}.\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2022}-\dfrac{1}{2023}\right)\)

\(A=\dfrac{2023}{1}.\left(1-\dfrac{1}{2023}\right)\)

\(A=\dfrac{2023}{1}.\dfrac{2022}{2023}\)

\(A=1.2022\)

\(A=2022\)

Vậy \(A=2022\)

b: Đặt \(A=\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{100}}\)

=>\(2A=1+\dfrac{1}{2}+...+\dfrac{1}{2^{99}}\)

=>\(2A-A=1+\dfrac{1}{2}+...+\dfrac{1}{2^{99}}-\dfrac{1}{2}-...-\dfrac{1}{2^{100}}\)

=>\(A=1-\dfrac{1}{2^{100}}< 1\)

2A ạ

a: Trên tia Ox, ta có: OB<OA

nên B nằm giữa O và A

=>OB+BA=OA

=>BA+4=10

=>BA=6(cm)

M là trung điểm của BA

=>\(MB=MA=\dfrac{BA}{2}=3\left(cm\right)\)

Vì M nằm giữa B và A

và B nằm giữa O và A

nên B nằm giữa O và M

=>OM=OB+BM=4+3=7(cm)

b: B là trung điểm của MN

=>\(MN=2\cdot MB=2\cdot3=6\left(cm\right)\)

Vì MN<MO

nên N nằm giữa M và O

=>MN+NO=MO

=>NO+6=7

=>NO=1(cm)

   Olm chào em đây là dạng toán nâng cao chuyên đề giá mua và giá bán, cấu trúc thi chuyên, thi học sinh giỏi. Hôm nay Olm.vn sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp giải ngược như sau:

                                   Giải:

                     3 420 000 đồng ứng với: 

                  100% - 5%  = 95% giá sau khi hạ lần thứ nhất

                  Giá sau khi hạ lần thứ nhất là:

                    3420  000 x 100 :  95  = 3 600 000 (đồng)

                      3 600 000 đồng ứng với:

                        100% - 10% = 90% (giá lúc đầu)

                    Giá lúc đầu của chiếc ti vi là:

                      3 600 000 x 100 : 90 = 4 000 000 (đồng)

                  Kết luận: ban đầu, chiếc ti vi có giá là 4 000 000 đồng.

a) Số học sinh loại giỏi:

120 . 1/6 = 20 (học sinh)

Số học sinh khá:

120 . 30% = 36 (học sinh)

Số học sinh trung bình:

120 . 1/3 = 40 (học sinh)

Số học sinh yếu:

120 - 20 - 36 - 40 = 24 (học sinh)

b) Tỉ số phần trăm của số học sinh yếu so với cả lớp:

24 . 100% : 120 = 20%

\(\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{99.100}\)

\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\)

\(=\dfrac{1}{2}-\dfrac{1}{100}\)

\(=\dfrac{50}{100}-\dfrac{1}{100}=\dfrac{49}{100}\)

=1- 1/2+1/2 - 1/3+1/3 - ... -1/99+1/99-1/100

=1-1/100

=99/100

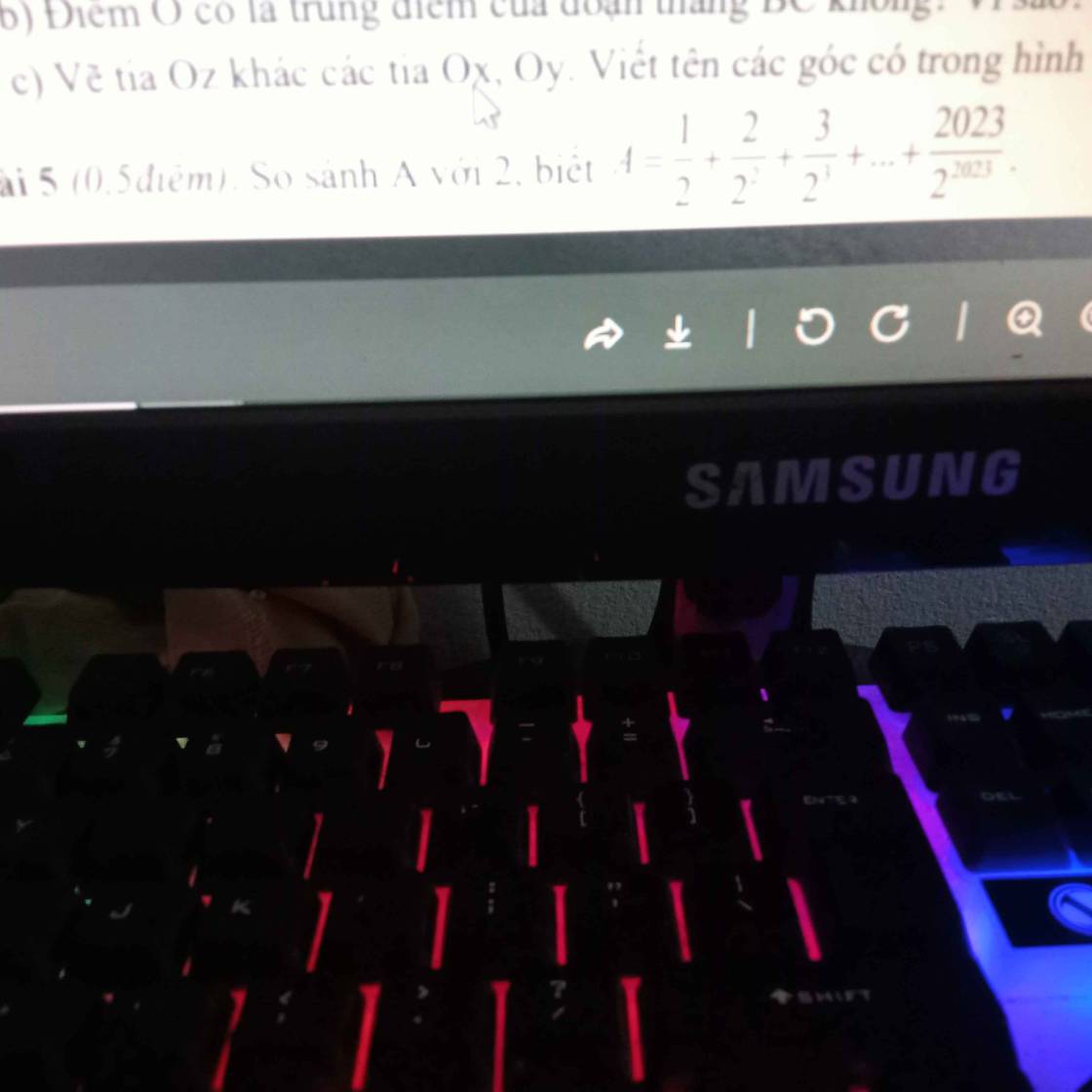
\(A=\dfrac{1}{2^1}+\dfrac{2}{2^2}+\dfrac{3}{2^3}+...+\dfrac{2023}{2^{2023}}\)

\(\Rightarrow2A=1+\dfrac{2}{2^1}+\dfrac{3}{2^2}+...+\dfrac{2023}{2^{2022}}\)

Trừ vế cho vế:

\(\Rightarrow2A-A=1+\dfrac{1}{2^1}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2022}}-\dfrac{2023}{2^{2023}}\)

\(\Rightarrow A=1+\dfrac{1}{2^1}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2022}}-\dfrac{2023}{2^{2023}}\)

\(\Rightarrow2A=2+1+\dfrac{1}{2^1}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2021}}-\dfrac{2023}{2^{2022}}\)

Trừ vế cho vế:

\(2A-A=2-\dfrac{2024}{2^{2022}}+\dfrac{2023}{2^{2023}}\)

\(\Rightarrow A=2-\dfrac{1}{2^{2022}}\left(2024-\dfrac{2023}{2}\right)\)

\(\Rightarrow A=2-\dfrac{2025}{2^{2023}}< 2\)

Vậy \(A< 2\)

\(\dfrac{2}{3}+\dfrac{1}{3}\cdot\left(-\dfrac{2}{3}+\dfrac{5}{6}\right):\dfrac{2}{3}\)

\(=\dfrac{2}{3}+\dfrac{1}{3}\cdot\dfrac{1}{6}:\dfrac{2}{3}\)

\(=\dfrac{2}{3}+\dfrac{1}{18}\cdot\dfrac{3}{2}\)

\(=\dfrac{2}{3}+\dfrac{1}{12}=\dfrac{9}{12}=\dfrac{3}{4}\)

3 phần 4

a, xác suất thực nghiệm xuất hiện mặt 2 chấm là : 

                       3:16=3/16

b,     xác suất thực nghiệm xuất hiện mặt n là : 

                           16:30=16/30

a, 3

b,6