Bạn xem lại đề bài, pt thiếu dấu "="

1.

Gọi B là ảnh của A qua phép tịnh tiến \(\overrightarrow{v}\)

Theo công thức tọa độ phép tịnh tiến:

\(\left\{{}\begin{matrix}x_B=-4+3=-1\\y_B=-9+\left(-7\right)=-16\end{matrix}\right.\)

\(\Rightarrow B=\left(-1;-16\right)\)

2.

Giả sử \(T_{\overrightarrow{u}}\left(d\right)=d'\Rightarrow d||d'\)

\(\Rightarrow\) Phương trình d' có dạng: \(3x-7y+c=0\) (1)

Lấy \(M\left(-2;0\right)\in d\)

Gọi \(T_{\overrightarrow{u}}\left(M\right)=M'\Rightarrow M'\in d'\)

Theo công thức phép tịnh tiến:

\(\left\{{}\begin{matrix}x_{M'}=-2+10=8\\y_{M'}=0+\left(-3\right)=-3\end{matrix}\right.\)

Thế vào (1) ta được: \(3.8-7.\left(-3\right)+c=0\Rightarrow c=-45\)

Vậy pt d' có dạng: \(3x-7y-45=0\)

3.

Đường tròn (C) có tâm \(I\left(-2;4\right)\) bán kính \(R=4\)

Gọi \(T_{\overrightarrow{v}}\left(C\right)=\left(C'\right)\Rightarrow\left(C'\right)\) là đường tròn có bán kính R và tâm \(I'\left(a';b'\right)\) là ảnh của I qua phép tịnh tiến \(\overrightarrow{v}\)

\(\Rightarrow\left\{{}\begin{matrix}x'=-2+\left(-7\right)=-9\\y'=4+\left(-1\right)=3\end{matrix}\right.\) 

\(\Rightarrow I'\left(-9;3\right)\)

Phương trình (C') có dạng:

\(\left(x+9\right)^2+\left(y-3\right)^2=16\)

4.

Đường tròn (C) tâm \(I\left(-1;2\right)\) bán kính \(R=\sqrt{\left(-1\right)^2+2^2-\left(-15\right)}=\sqrt{20}\)

Lý luận tương tự câu trên, ta có:

\(\left\{{}\begin{matrix}x'=-1+\left(-4\right)=-5\\y'=2+5=7\end{matrix}\right.\)

Phương trình (C') có dạng:

\(\left(x+5\right)^2+\left(y-7\right)^2=20\)

`a)` H/s xác định `<=>x+2 \ne 0<=>x \ne -2`

 `=>TXĐ: D=R\\{-2}`

___________________________

`b)` H/s xác định `<=>x^2-3x+2 >= 0<=>[(x <= 1),(x >= 2):}`

  `=>TXĐ: D=(-oo;1]uu[2;+oo)`

___________________________

`c)` H/s xác định `<=>cos 2x \ne 0<=>2x \ne \pi/2+k\pi`

                            `<=>x \ne \pi/4+k\pi/2`  `(k in ZZ)`

  `=>TXĐ: D=RR\\{\pi/4+k\pi/2, k in ZZ}`

___________________________

`d)` H/s xác định `<=>sin x \ne 0<=>x \ne k\pi`  `(k in ZZ)`

  `=>TXĐ: D=RR\\{k\pi,k in ZZ}`

H/s xác định `<=>` $\begin{cases} sin x - 1 \ne 0\\cos x \ne 0 \end{cases}$

                    `<=>` $\begin{cases} sin x \ne 1\\cos x \ne 0 \end{cases}$

                   `<=>cos x \ne 0<=>x \ne` \(\dfrac{\pi}{2}+k\pi\)

  `=>TXĐ: D=R` \ {\(\dfrac{\pi}{2}+k\pi\),k in ZZ}

ĐKXĐ: \(\left\{{}\begin{matrix}sinx\ne0\\sinx\ne1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne k\pi\\x\ne\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)

lưu ý đây ko phải là toán lớp 11

B đúng (Y là trường hợp riêng của X ứng với các giá trị n chẵn)

You can learn the difficult concept to understand from Solvemate. This is a education service for using technology to adapt in order to create mathematical problems based on the learning needs of students.
Math mate in your pocket. https://intro.solve-mate.com/

x=30

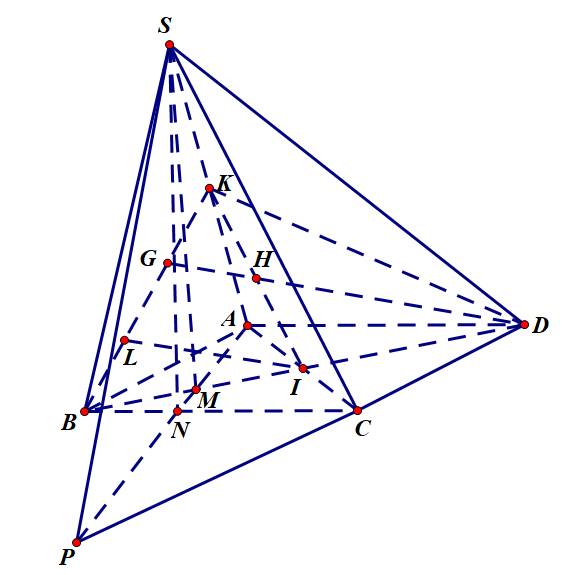
a) ta có S là điểm chung thứ nhất của mặt (SAM) và (SBC)

trong mặt phẳng (ABCD) gọi N là giao điểm của AM và BC => N là điểm chung thứ hai của mặt (SAM) và (SBC)

=> giao tuyến của mặt (SAM) và (SBC) là SN.

b) ta có S là điểm chung thứ nhất của mặt (SAM) và (SDC)

trong mặt phẳng (ABCD) gọi P là giao điểm của AM và DC => P là điểm chung thứ hai của mặt (SAM) và (SDC)

=> giao tuyến của mặt (SAM) và (SBC) là SP.

c) Gọi K là trung điểm SA, G là trọng tâm tam giác SAB => BG = 2/3 BK.

Xét mặt phẳng phụ (BKD) chứa DG và mặt phẳng (SAC)

có điểm chung thứ nhất là K.

nối KI cắt DG tại H => H là điểm chung thứ hai của mặt (BKD) và (SAC) hay H là giao điểm của DG và (SAC) 

ta có L là trung điểm BG (gt)

I trung điểm BD 

=> LI // DG (đường trung bình)

hay LI // GH

xét tam giác KLI có LI // GH và G là trung điểm KL (gt)

=> H là trung điểm KI.

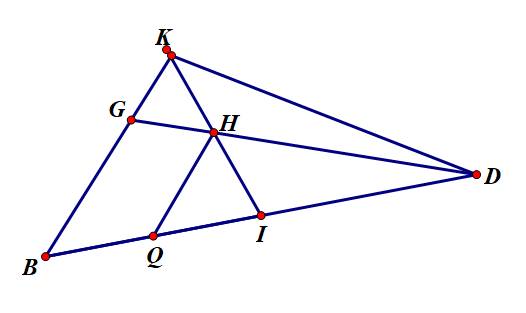
trong mặt phẳng (KBD) gọi HQ // AB (Q thuộc BD)

xét tam giác ABI có HQ // AB, H là trung điểm AI => Q là trung điểm BI (đường trung bình)

áp dụng định lý talet trong tam giác BDG ta được: DH/DG = DQ/DB = 3/4

vậy DH/DG = 3/4

*a trình bày rõ hết sức có thể rùi đó, e không hiểu chỗ nào thì có thể hỏi a nha :D

cho anh sửa lại dòng thứ 4 từ dưới lên nha, "xét tam giác KBI có HQ//AB..." chứ không phải "xét tam giác ABI ..." nhé :*>

\(0\le x\le\pi\Rightarrow\dfrac{\pi}{3}\le x+\dfrac{\pi}{3}\le\dfrac{4\pi}{3}\)

\(\Rightarrow y_{max}=\dfrac{1}{2}\) khi \(x+\dfrac{\pi}{3}=\dfrac{\pi}{3}\Leftrightarrow x=0\)

\(y_{min}=-1\) khi \(x+\dfrac{\pi}{3}=\pi\Leftrightarrow x=\dfrac{2\pi}{3}\)

ry5yrerwwkewwwdwjwkjdjwkwe