cho tam giac ABC nội tiếp đường tròn tâm 0 gọi D là điểm chính giữa của cung nhỏ BC 2 tiếp tuyến C VÀ D với dg tròn tâm o cắt nhau tại E gọi P Q lần lượt là các giao điểm của các cặp dg thẳng AB và CD   AD và

CMR BC//DE

tứ giác CODE APQC nội tiếp đường tròn

tìm điều kiện của tam giác ABC để góc AQP=90

ĐK...

đặt \(\sqrt{x^2-x-6}=a\left(a\ge0\right)\)

Ta có pt <=> \(a^2+a-12=0\Leftrightarrow\left(a+4\right)\left(a-3\right)=0\Leftrightarrow a-3=0\left(vi:a+3>0\right)\)

đến đây tự làm nhá 

8n

a) thay m=-1 vào pt(1) có : (-1+1)x² -(2.1+3)x+1+4=0

\(\Leftrightarrow-5x+5=0\)

\(\Leftrightarrow-5.\left(x-1\right)=0\)

\(\Leftrightarrow x=1\)

vậy ....

b) ĐK pt(1) : m+1\(\ne0\)\(\Leftrightarrow m\ne-1\)

\(\Delta=b^2-4ac=[-\left(2m+3\right)]^2-4.\left(m+1\right).\left(m+4\right)\)

........

bạn cho mik cái nhé

a) Ta có: Điểm K đối xứng với điểm F qua AC => FC=KC;  AF=AK 

=> \(\Delta\)ACF=\(\Delta\)ACK (c.c.c) => ^AFC=^AKC (2 góc tương ứng) 

Ta thấy tứ giác ABFC nội tiếp đường tròn tâm O => ^AFC=^ABC.

H là trực tâm của tam giác ABC => CH\(\perp\)AB (tại D)

=> ^HCB + ^ABC = 90⁰ (1)

 Lại có AH\(\perp\)BC => ^LHC + ^HCB = 90⁰ (2)

Từ (1) và (2) => ^ABC=^LHC. Mà ^LHC + ^AHC = 180⁰

=> ^ABC + ^AHC = 180⁰. Do ^ABC=^AFC=^AKC (cmt) => ^AKC + ^AHC= 180⁰

Xét tứ giác AHCK có: ^AKC + ^AHC =180⁰ => Tứ giác AHCK nội tiếp đường tròn (đpcm).

b) AO cắt GI tại Q

Gọi giao điểm của AO và (O) là P = >^ACP=90⁰ => ^CAP+^CPA=90⁰ (*)

Thấy tứ giác ACPB nội tiếp đường tròn (O) => ^CPA=^ABC 

Mà ^ABC+^AHC=180⁰ => ^CPA+^AHC=180⁰ (3).

Ta có tứ giác AHCK là tứ giác nội tiếp (cmt) => ^KAI=^CHI

Lại có \(\Delta\)ACF=\(\Delta\)ACK => ^FAC=^KAC hay ^KAI=^GAI  => ^GAI=^CHI

Xét tứ giác AHGI: ^GAI=^GHI (=^CHI) (cmt) = >Tứ giác AHGI nội tiếp đường tròn

=> ^AIG+^AHG=180⁰ hay ^AIG + ^AHC=180⁰ (4)

Từ (3) và (4) => ^AIG=^CPA (**)

Từ (*) và (**) => ^CAP+^AIG=90⁰ hay ^IAQ+^AIQ=90⁰ => \(\Delta\)AIQ vuông tại Q

Vậy AO vuông góc với GI (đpcm).

a) Có A4100 = 94109400 kết quả có thể.

b) Nếu giải nhất đã xác định thì 3 giải nhì,ba,tư rơi vào 99 người còn lại. Vậy có A399 = 941094 kết quả có thể.

c) Người giữ vé số 47 có 4 khả năng trúng 1 trong 4 giải. Sau khi xác định giải của người này thì 3 giải còn lại rơi vào 99 người không giữ vé số 47. Vậy theo quy tắc nhân có 4.A399 = 3764376 kết quả có thể.

a) Có A4100 = 94109400 kết quả có thể.

b) Nếu giải nhất đã xác định thì 3 giải nhì,ba,tư rơi vào 99 người còn lại. Vậy có A399 = 941094 kết quả có thể.

c) Người giữ vé số 47 có 4 khả năng trúng 1 trong 4 giải. Sau khi xác định giải của người này thì 3 giải còn lại rơi vào 99 người không giữ vé số 47. Vậy theo quy tắc nhân có 4.A399 = 3764376 kết quả có thể.

a) Số cách chọn ra 4 người điểm cao nhất trong 15 người tham dự là số tổ hợp chập 4 của 15 phần tử. Vậy có C415 = 1365 kết quả.

b) Số cách chọn ra 3 giải nhất, nhì, ba là số chỉnh hợp chập 3 của 15 phần tử. vậy có \(Ạ^3_{15}\) = 2730 kết quả.

Chúc bạn hok tốt ~

a) kết quả sẽ chỉ có 1

b) có 3 kết quả 

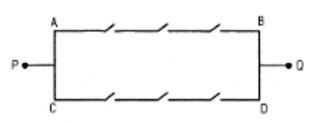
Mỗi cách đóng-mở 6 công tắc của mạng điện được gọi là một trạng thái của mạng điện. Theo quy tắc nhân, mạng điện có 2^6 = 64 trạng thái. Trước hết ta tìm xem có bao nhiêu trạng thái không đóng mạch (không có dòng điện đi qua). Mạch gồm 2 nhánh A → B và C → D . Trạng thái không thong mạch xảy ra khi và chỉ khi cả hai nhánh A → B và C → D đều không thông mạch. Dễ thấy nhánh A → B có 8 trạng thái trong đó có duy nhất 1 trạng thái thông mạch còn 7 trạng thái còn lại đều không thong mạch. Tương tự ở nhánh C → D có 7 trạng thái không thong mạch. Theo quy tắc nhân ta có 7.7 = 49 trạng thái mà cả A → B và C → D đều không thong mạch. Vậy mạng điện có 64 - 49 = 15 trạng thái thong mạch từ P đến Q.

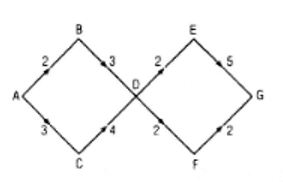
Có 4 phương án đi qua các tỉnh A đến G là:

a) A → B → D → E → G

b) A → B → D → F → G

c) A → C → D → E → G

d) A → C → D → F → G

Theo quy tắc nhân ta có:

Phương án a) có 2.3.2.5 = 60 cách đi

Phương án b) có 2.3.2.2 = 24 cách đi

Phương án c) có 3.4.2.5 = 120 cách đi

Phương án d) có 3.4.2.2 = 48 cách đi

Vậy theo quy tắc cộng có 60 + 24 + 120 + 48 = 252 cách đi từ A đến G.

Có 4 phương án đi qua các tỉnh A đến G là :

a. A → B → D → E → G

b. A → B → D → F → G

c. A → C → D → E → G

d. A → C → D → F → G

Theo quy tắc nhân, ta có :

Phương án a có 2.3.2.5=60 cách đi;

Phương án b có 2.3.2.2=24 cách đi;

Phương án c có 3.4.2.5=120 cách đi;

Phương án d có 3.4.2.2=48 cách đi.

Theo quy tắc cộng, ta có : 60+24+120+48=252 cách đi từ A đến G.

Một số tự nhiên có 4 chữ số chia hết cho 5 có dạng:

\(\overline{abcdeg}\)

Với a có 9 cách chọn, g có 2 cách chọn và b,c,d,e mỗi số có 10 cách chọn. Vậy theo quy tắc nhân có 9.104.2 = 180000 số.

trường hợp 1: chữ số cuối cùng là 0
thì có 9.10.10.10.10=9.10^4 số
th 2: chữ số cuối cùng là 5=> có 9.10.10.10.10=9.10^4 số
vậy có 9.10^4+9.10^4 =180000 số

a) Số cách chọn 3 người mà không có sự phân biệt về chức vụ trong ban thường vụ bằng số tổ hợp chập 3 của 7 phần tử và bằng C37 = 35 cách chọn.

b) Số cách chọn 3 người với các chức vụ : Bí thư, phó bí thư, ủy viên bằng số chỉnh hợp chập 3 của 7 phần tử và bằng A37 = 210 cách chọn.

Chúc bạn hk tốt ~