Gọi x là số đo cung nhỏ AB (x > 0)

Số đo cung lớn AB là 2x

Ta có:

x + 2x = 360⁰

3x = 360⁰

x = 360⁰ : 3

x = 120⁰

⇒ ∠AOB = 120⁰

∆AOB có:

OA = OB = R

⇒ ∆AOB cân tại O

⇒ ∠OAB = ∠OBA = (180⁰ - ∠AOB) : 2

= (180⁰ - 120⁰) : 2

= 30⁰

Ta có hình vẽ sau:

Vẽ đường cao OH của ∆OAB

⇒ ∆OAH vuông tại H

⇒ cosOAH = AH : OA

⇒ AH = OA.cosOAH

= R.cos30⁰

Do OH ⊥ AB

⇒ H là trung điểm của AB

⇒ AB = 2AH

Ta có: \(\widehat{ABC}=90^0\)

=>B nằm trên đường tròn đường kính AC(1)

Ta có: \(\widehat{ADC}=90^0\)

=>D nằm trên đường tròn đường kính AC(2)

Từ (1),(2) suy ra B,D cùng nằm trên đường tròn đường kính AC

=>A,B,C,D cùng thuộc đường tròn tâm O, đường kính AC

Xét (O) có

AC là đường kính

BD là dây

Do đó: BD<AC

Xét tứ giác BC'B'C có \(\widehat{BC'C}=\widehat{BB'C}=90^0\)

nên BC'B'C là tứ giác nội tiếp đường tròn đường kính BC

=>BC'B'C là tứ giác nội tiếp đường tròn tâm O, đường kính BC

Xét (O) có

BC là đường kính

B'C' là dây

Do đó: B'C'<BC

Gọi OH là khoảng cách từ O đến dây MN

=>OH\(\perp\)MN tại H

ΔOMN cân tại O

mà OH là đường cao

nên H là trung điểm của MN

=>\(HM=HN=\dfrac{R}{2}\)

ΔOHM vuông tại H

=>\(OH^2+HM^2=OM^2\)

=>\(OH^2=R^2-\left(\dfrac{R}{2}\right)^2=\dfrac{3R^2}{4}\)

=>\(OH=\sqrt{\dfrac{3R^2}{4}}=\dfrac{R\sqrt{3}}{2}\)

=>Khoảng cách từ O đến dây MN là \(\dfrac{R\sqrt{3}}{2}\)

Gọi giao điểm của MN với OA là H

Vì MN\(\perp\)OA tại trung điểm của OA

nên MN\(\perp\)OA tại H và H là trung điểm của OA

Xét ΔOMA có 

MH là đường cao

MH là đường trung tuyến

Do đó: ΔOMA cân tại M

=>MO=MA

mà OM=OA

nên OM=MA=OA

=>ΔOMA đều

=>\(\widehat{MOA}=60^0\)

Xét ΔMHO vuông tại H có \(sinMOH=\dfrac{MH}{MO}\)

=>\(\dfrac{MH}{10}=sin60=\dfrac{\sqrt{3}}{2}\)

=>\(MH=10\cdot\dfrac{\sqrt{3}}{2}=5\sqrt{3}\left(cm\right)\)

ΔOMN cân tại O

mà OH là đường cao

nên H là trung điểm của MN

=>\(MN=2\cdot MH=2\cdot5\sqrt{3}=10\sqrt{3}\left(cm\right)\)

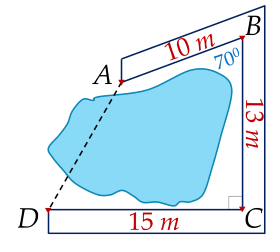
`DE = DB . sinB = 10. sin70^o ~~ 9,4 (m) `

`=> AF ~~ 15 - 9,4~~ 5,6 (m) `

`ΔAFD` vuông tại `F `

`=> AD = sqrt{AF^2 + DF^2} = sqrt{AF^2 + EC^2} = sqrt{5,6^2 + 13^2} ~~14,15 (m)`

Vậy ....

a) Nhiệt độ t (⁰C) tuần tới tại Tokyo là:

t > -5

b) Gọi x (tuổi) là tuổi của người điều khiển xe máy điện. Ta có bất đẳng thức:

x ≥ 16

c) Gọi z (đồng) là mức lương tối thiểu trong một giờ làm việc của người lao động. Ta có bất đẳng thức:

z ≥ 20000

d) y là số dương nên ta có bất đẳng thức:

y > 0

a, t>5

b,x≥16

c,mức lương tối thiểu≤20 000đ

d, y>0

a) ĐKXĐ: x ≠ -5

Phương trình đã cho trở thành:

(x + 6).2 + 3.(x + 5) = 2.2(x + 5)

2x + 12 + 3x + 15 = 4x + 20

5x - 4x = 20 - 12 - 15

x = -7 (nhận)

Vậy S = {-7}

b) x + 3y = -2

x = -2 - 3y (1)

5x + 8y = 11 (2)

Thế (1) vào (2), ta được:

5(-2 - 3y) + 8y = 11

-10 - 15y + 8y = 11

-7y = 11 + 10

-7y = 21

y = 21 : (-7)

y = -3

Thế y = -3 vào (1), ta được:

x = -2 - 3.(-3) = 7

Vậy S = {(7; -3)}

Gọi vận tốc lúc về của người đó là x(km/h)

(Điều kiện: x>0)

Vận tốc lúc đi là x+10(km/h)

Thời gian người đó đi từ A đến B là \(\dfrac{60}{x+10}\left(giờ\right)\)

Thời gian người đó đi từ B về A là \(\dfrac{60}{x}\left(giờ\right)\)

Thời gian về nhiều hơn thời gian đi là 30p=0,5 giờ nên ta có:

\(\dfrac{60}{x}-\dfrac{60}{x+10}=0,5\)

=>\(\dfrac{60x+600-60x}{x\left(x+10\right)}=0,5\)

=>\(x\left(x+10\right)=\dfrac{600}{0,5}=1200\)

=>\(x^2+10x-1200=0\)

=>(x+40)(x-30)=0

=>\(\left[{}\begin{matrix}x+40=0\\x-30=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-40\left(loại\right)\\x=30\left(nhận\right)\end{matrix}\right.\)

Vậy: Vận tốc lúc về của người đó là 30km/h

1) sin35⁰ = cos(90⁰ - 35⁰) = cos55⁰

Vậy sin35⁰ = cos55⁰

tan35⁰ = cot(90⁰ - 35⁰) = cot55⁰

Vậy tan35⁰ = cot55⁰

2) ∆ABC vuông tại A (gt)

⇒ AB = BC.cosB

= 20.cos36⁰

≈ 16,18 (cm)