Trong không gian Oxyz, cho 2 điểm A(2;1;0) và B(0;4;0). Xét điểm S thay đổi luôn thuộc trục Oz; gọi K là trung điểm SB, H là hình chiếu vuông góc của O trên AK. Biết rằng H luôn thuộc một đường tròn cố định, chu vi của đường tròn đó là bao nhiêu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề thi đánh giá năng lực

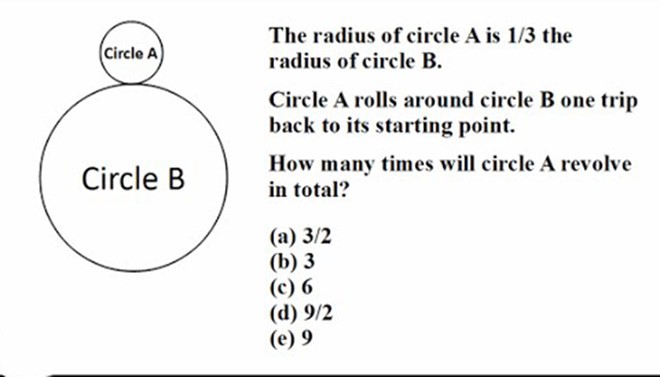
There are no correct choice.
You can make a visual proof. Cut 2 round pieces of paper such that a piece has the radius 3 times the other's paper's radius. Then, carefully roll the smaller pieces around the larger piece, and you can see that the smaller circle has to make 4 revolutions in order to get back to its starting point.

ĐKXĐ: \(0< x\le2\)
\(log_2x-2log_2x-4\sqrt{1-log_2x}=m\)
\(\Leftrightarrow\left(1-log_2x\right)^2-4\sqrt{1-log_2x}-1=m\)
Đặt \(\sqrt{1-log_2x}=t\ge0\)
\(\Rightarrow t^4-4t-1=m\)
Xét hàm \(f\left(t\right)=t^4-4t-1\) có \(f'\left(t\right)=4t^3-4=0\Rightarrow t=1\)
BBT:
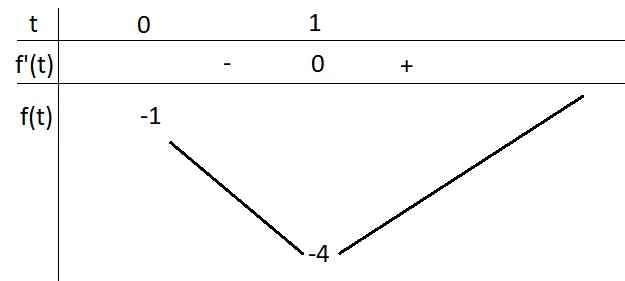
Từ đó ta thấy \(f\left(t\right)=m\) có nghiệm khi \(m\ge-4\)
\(\Rightarrow\) Có 2024 giá trị nguyên của m thỏa mãn

\(\sqrt{2^{90}}-2^{45}\\ =\sqrt{4^{45}}-2^{45}\\ =2^{45}-2^{45}=0\)
\(\sqrt{2^{90}}\) - 245
= \(\sqrt{\left(2^{45}\right)}^2\) - 245
= 245 - 245
= 0