Lời giải:

1. Dấu giữa (x+3) và (2x+3)² là gì vậy bạn?

2.

$E=(4x^2-12x)-(x^2-10x+25)-3(x+1)^2+4(x+1)^2-4x^2+5$

$=4x^2-12x-x^2+10x-25+(x+1)^2-4x^2+5$

$=4x^2-12x-x^2+10x-25+x^2+2x+1-4x^2+5$

$=(4x^2-x^2+x^2-4x^2)+(-12x+10x+2x)+(-25+1+5)$

$=-19$ là giá trị không phụ thuộc vào biến (đpcm)

a/

\(\widehat{ADB}=\widehat{CDB}=\dfrac{\widehat{ADC}}{2}\)  (gt)

Mà \(\widehat{ADC}=\widehat{BCD}\) (góc ở đáy hình thang cân)

\(\Rightarrow\widehat{CDB}=\dfrac{\widehat{BCD}}{2}\)

Xét tg vuông BCD có

\(\widehat{CDB}+\widehat{BCD}=90^o\Rightarrow\dfrac{\widehat{BCD}}{2}+\widehat{BCD}=90^o\Rightarrow\widehat{BCD}=60^o\)

\(\Rightarrow\widehat{CDB}=\dfrac{\widehat{BCD}}{2}=\dfrac{60^o}{2}=30^o\)

\(\Rightarrow\widehat{ADC}=\widehat{BCD}=60^o\)

Ta có

\(\widehat{DAB}=\widehat{ABC}\) (góc ở đáy hình thang cân)

\(\widehat{DAB}=180^o-\widehat{ADC}=180^o-60^o=120^o\)

\(\Rightarrow\widehat{DAB}=\widehat{ABC}=120^o\)

b/ Từ B dựng đường thẳng // AD cắt CD tại E ta có

AB // CD => AD//DE mà BE//AD

=> ABED là hình bình hành

=> BE = AD mà AD = BC (cạnh bên hình thang cân)

=> BE = AD = BC = 6 cm

Xét tg BCE có

BE = BC => tg BCE cân tại B

\(\Rightarrow\widehat{BEC}=\widehat{BCD}=60^o\Rightarrow\widehat{CBE}=60^o\) => tg BCE là tg giác đều

=> BE = CE = BC = 6 cm

Xét tg vuông BCD có

\(\widehat{CDB}=30^o\) (cmt) => \(BC=\dfrac{CD}{2}\) (trong tg vuông cạnh đối diện với góc 30 độ bằng nửa cạnh huyền)

\(\Rightarrow CD=2BC=2.6=12cm\)

\(\Rightarrow DE=CD-CE=12-6=6cm\)

Mà DE = AB = 6 cm (cạnh đối hbh ABED)

\(\Rightarrow C_{ABCD}=AB+BC+CD+AD=6+6+12+6=30cm\)

Ta có DB là tia pgiac của \(\widehat{ADC}\)

Mà \(\widehat{ADC}=\widehat{BCD}\) do 2 góc là góc đáy của hình thang

=>\(\widehat{BDC}=\widehat{DCB}:2\)

Xét ∆ vuông BDC có:

\(\widehat{BDC}+\widehat{DCB}=90^o=>\widehat{DCB}:2+\widehat{DCB}=90^o\)

\(\Rightarrow\widehat{DCB}=60^o\\ \Rightarrow\widehat{BDC}=60^o:2=30^O\)

Ta có: \(\widehat{BAD}=\widehat{ABC}\) (t/chất hthang)

\(\Rightarrow\widehat{BAD}=180^o-\widehat{BDC}=180^o-60^o=120^o\)

\(\Rightarrow\widehat{BAD}=\widehat{ABC}=120^o\)

a) \(A=\left(x+5\right)^2-\left(x+3\right)^2\)

\(=\left[\left(x+5\right)-\left(x+3\right)\right]\left[\left(x+5\right)+\left(x+3\right)\right]\)

\(=\left(x+5-x-3\right)\left(x+5+x+3\right)\)

\(=2\left(2x+8\right)\)

\(=4x+16\)

b) \(B=\left(4x+1\right)^2-\left(2x+1\right)^2\)

\(=\left[\left(4x+1\right)-\left(2x+1\right)\right]\left[\left(4x+1\right)+\left(2x+1\right)\right]\)

\(=\left(4x+1-2x-1\right)\left(4x+1+2x+1\right)\)

\(=2x\left(6x+2\right)\)

\(=12x^2+4x\)

c) \(C=\left(3-4x\right)^2-\left(2x-1\right)\left(8x-9\right)\)

\(=9-24x+16x^2-16x^2+18x+8x-9\)

\(=\left(16x^2-16x^2\right)+\left(-24x+18x+8x\right)+\left(9-9\right)\)

\(=2x\)

d) \(D=\left(4+2x^2\right)-\left(1-4x\right)\left(4-x\right)\)

\(=4+2x^2-4+x+16x-4x^2\)

\(=\left(2x^2-4x^2\right)+\left(x+16x\right)+\left(4-4\right)\)

\(=-2x^2+17x\)

e) \(E=\left(2-3x\right)^2-2\left(2-3x\right)\left(3x+5\right)+\left(3x+5\right)^2\)

\(=\left(2-3x+3x+5\right)^2\)

\(=7^2\)

\(=49\)

a/

AB = AC => tg ABC cân tại A \(\Rightarrow\widehat{ACB}=\widehat{ABC}\) 

Xét tg ABC có

\(\widehat{DAB}=\widehat{ABC}+\widehat{ACB}\) (trong tg số đo góc ngoài bằng tổng số đo hai góc trong khồng kề với nó)

\(\Rightarrow\widehat{DAB}=\widehat{ACB}+\widehat{ACB}=2\widehat{ACB}\)

b/

AC = AD (gt); MD = MB (gt) => MA là đường trung bình của tg DBC

=> MA//BC

c/

\(AH\perp BC\) (gt); tg ABC cân tại A (cmt) => HB = HC (trong tg cân đường cao hạ từ đỉnh tg cân đồng thời là đường trung tuyến)

AC = AD (gt)

=> HA là đường trung bình của tg DBC => AH//BD

Bài 5

\(\widehat{A}+\widehat{D}=180^o\) (Hai góc trong cùng phía bù nhau)

\(\widehat{DAx}=\widehat{BAx}=\dfrac{\widehat{A}}{2}\) (gt)

\(\widehat{ADy}+\widehat{CDy}=\dfrac{\widehat{D}}{2}\) (gt)

\(\Rightarrow\widehat{DAx}+\widehat{ADy}=\dfrac{\widehat{A}}{2}+\dfrac{\widehat{D}}{2}=\dfrac{180^o}{2}=90^o\)

Xét tg ADE có

\(\widehat{AED}=180^o-\left(\widehat{DAx}+\widehat{ADy}\right)=180^o-90^o=90^o\) (Tổng các góc trong của tg bằng 180 độ)

\(\Rightarrow Ax\perp Dy\)

Bài 6:

a/

Ta có

AB//CD => AB//DE

BE//AB (gt)

=> ABED là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)

=> AB = DE; AD = BE (Trong hình bình hành các cạnh đối nhau thì bằng nhau)

b/

CD - DE = CE

Mà AB = DE (cmt)

=> CD - AB = CE

c/

Xét tg BCE có

BC+BE>CE (trong tg tổng độ dài 2 cạnh lớn hơn độ dài cạnh còn lại)

Mà CE = CD - DE và DE = AB (cmt) và BE = AD

=> BC+BE = BC + AD>CE = CD - AB

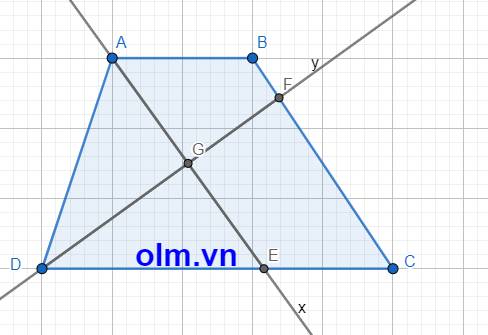
Gọi G là giao điểm của hai đường phân giác Ax và By 

Ta có: \(\widehat{ADG}\) = \(\dfrac{1}{2}\)\(\widehat{ADE}\) ( vì DG là phân giác góc ADE)

           \(\widehat{DAG}\) = \(\dfrac{1}{2}\)\(\widehat{DAB}\)( vì AG là phân giác góc DAB )

     ⇒ \(\widehat{ADG}\) + \(\widehat{DAG}\) = \(\dfrac{1}{2}\)\(\widehat{ADE}\) + \(\dfrac{1}{2}\)\(\widehat{DAB}\) = \(\dfrac{1}{2}\)(\(\widehat{ADE}\) + \(\widehat{DAB}\)) 

           \(\widehat{ADE}\) + \(\widehat{DAB}\) = 180⁰ (vì hai góc là hai góc trong cùng phía)

      ⇒ \(\widehat{ADG}\) + \(\widehat{DAG}\) = \(\dfrac{1}{2}\) \(\times\) 180⁰ = 90⁰

          Xét tam giác ADG có: \(\widehat{GAD}\) + \(\widehat{ADG}\) + \(\widehat{DGA}\) = 180⁰ (tổng ba góc trong 1 tam giác bằng 180⁰)

               ⇒ \(\widehat{DGA}\)  = 180⁰ - 90⁰ = 90⁰

Vậy tam giác ADG vuông tại G ⇒AE \(\perp\) DG (đpcm)

\(P=\dfrac{1}{abc}+\dfrac{1}{a^2+b^2+c^2}=\dfrac{a+b+c}{abc}+\dfrac{1}{a^2+b^2+c^2}\)

\(=\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ac}+\dfrac{1}{a^2+b^2+c^2}\left(1\right)\)

\(\)\(\left\{{}\begin{matrix}a+b+c=1\\\left(a+b+c\right)^2=a^2+b^2+c^2+2ab+2bc+2ac\end{matrix}\right.\)

\(\Rightarrow\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ac}\ge\dfrac{9}{ab+bc+ac}\left(2\right)\)

\(\left(1\right),\left(2\right)\Rightarrow P\ge\dfrac{9}{ab+bc+ac}+\dfrac{1}{a^2+b^2+c^2}\)

\(=\dfrac{1}{2\left(ab+bc+ac\right)}+\dfrac{1}{a^2+b^2+c^2}+\dfrac{17}{2\left(ab+bc+ac\right)}\)

\(\Rightarrow P\ge\dfrac{9}{\left(a+b+c\right)^2}+\dfrac{17}{2\left(ab+bc+ac\right)}\)

\(\Rightarrow P\ge9+\dfrac{17}{2\left(ab+bc+ac\right)}\)

mà \(ab+bc+ac\le\dfrac{\left(a+b+c\right)^2}{3}=\dfrac{1}{3}\)

\(\Rightarrow P\ge9+\dfrac{17}{2.\dfrac{1}{3}}=9+\dfrac{17.3}{2}=\dfrac{18+17.3}{2}=\dfrac{69}{2}\)

\(\Rightarrow Min\left(P\right)=\dfrac{69}{2}\)

a, Số cách chọn chữ số hàng trăm: 9 (trừ số 0)

Số cách chọn chữ số hàng chục: 9 cách chọn (trừ chữ số hàng trăm)

Số cách chọn chữ số hàng đơn vị: 8 cách chọn (trừ chữ số hàng trăm, hàng chục)

Số phần tử của tập hợp C: 9 x 9 x 8 = 648 (phần tử)

b, BCNN(3;5)= 3 x 5 = 15

Từ 1 đến 15 có số lượng số chỉ chia hết cho 3 hoặc chỉ chia hết cho 5 là: 6 số (Các số: 3;6;9;12;5;10)

D là tập hợp các số tự nhiên không quá 1000 chỉ chia hết cho 3 hoặc chia hết cho 5

Số tự nhiên lớn nhất chia hết cho cả 3 và 5 mà không vượt quá 1000 là 990

Từ 990 đến 1000 có số lượng số chỉ chia hết cho 3 hoặc cho 5 là: 5 số (993; 995; 996; 999; 1000)

Số lượng phần tử của D:

(990 - 0): 15 x 6 + 5= 401 (phần tử)

Đáp số: 401 phần tử

xét tam giác ABH và Tam giác ACH có :

AC=AB(tính chất tam giác cân)

AHB=AHC(AH vg góc BC)

AH chung

do đó tam giác ABH=tam giác ACH(ch-gn)

b,tAm giác ABC có AH là đường cao xuất phát từ đỉnh A đồng thời là đường phân giác .Suy ra :góc BAH=CAH^(1) HAY EAH^=CAH^

vì EH //AC nên :CAH^=AHE^(2 góc sltrong)(2)

Từ (1) và(2) suy raEAH^=AHE^

suy ra tam giác AHE cân tại E

\(x+y=a\left(1\right)\)

\(x-y=b\left(2\right)\)

\(\left(1\right)+\left(2\right)\Rightarrow2x=a+b\Rightarrow x=\dfrac{a+b}{2}\)

\(\left(1\right)\Rightarrow y=a-x\Rightarrow y=a-\dfrac{a+b}{2}\Rightarrow y=\dfrac{a-b}{2}\)

\(xy=\dfrac{\left(a+b\right)}{2}.\dfrac{\left(a-b\right)}{2}=\dfrac{a^2-b^2}{4}\)

\(x^3-y^3=\left(\dfrac{a+b}{2}\right)^3-\left(\dfrac{a-b}{2}\right)^3=\dfrac{\left(a+b\right)^3}{8}-\dfrac{\left(a-b\right)^3}{8}\)

\(=\dfrac{\left(a+b\right)^3-\left(a-b\right)^3}{8}\)

\(=\dfrac{\left(a+b-a+b\right)\left[\left(a+b\right)^2+\left(a+b\right)\left(a-b\right)+\left(a-b\right)^2\right]}{8}\)

\(=\dfrac{2b\left[a^2+b^2+2ab+a^2-b^2+a^2+b^2-2ab\right]}{8}\)

\(=\dfrac{b\left[3a^2+b^2+2ab\right]}{4}\)

\(\left\{{}\begin{matrix}x+y=a\\x-y=b\end{matrix}\right.\) tính \(x^3\) - y³ theo \(a\) và \(b\)

⇒ \(\left\{{}\begin{matrix}x+y+x-y=a+b\\x-y=b\end{matrix}\right.\)

⇔ \(\left\{{}\begin{matrix}2x=a+b\\y=x-b\end{matrix}\right.\)

⇔ \(\left\{{}\begin{matrix}x=\left(a+b\right):2\\y=\left(a-b\right):2\end{matrix}\right.\) ⇒ \(xy\) = \(\dfrac{a+b}{2}\)\(\times\)\(\dfrac{a-b}{2}\) = \(\dfrac{a^2-b^2}{4}\)

\(x^{3^{ }}\) - y³ = (\(x\) - y)(\(x^2\) + \(x\)y + y²) = \(\left(x-y\right)\)\(\left(\left[x+y\right]^2-xy\right)\) (1)

Thay \(x-y\) = a; \(x\) + y = b và \(xy\) = \(\dfrac{a^2-b^2}{4}\) vào (1) ta có:

\(x^3\) - y³ = b.(a² - \(\dfrac{a^2-b^2}{4}\)) = b.\(\dfrac{3a^2+b^2}{4}\) = \(\dfrac{3a^2b+b^3}{4}\)

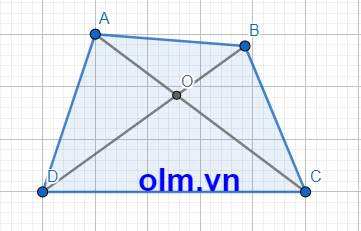
 a,  Xét \(\Delta\) AOB có: AO+OB > AB (trong tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)

Tương tự ta có:  OC + OD > DC

                           OA + OD > AD

                           OB + OC > BC 

Cộng vế với vế ta có:

OA+OB+OC+OD+OA+OD+OB+OC > AB +DC+AD+BC

(OA+OC)\(\times\)2 + (OB + OD)\(\times\)2 >  P_ABCD

AC \(\times\) 2 + BD \(\times\) 2 > P_ABCD

AC + BD > \(\dfrac{P_{ABCD}}{2}\) (đpcm)

b, Xét \(\Delta\) ABD có: AB + AD > BD (trong tam giác tổng hai cạnh bao giờ cũng lớn hơn cạnh còn lại)

Tương tự ta có:   AD + DC > AC 

                            DC + CB > DB 

                            CB + AB > AC 

  Cộng vế với vế ta có: 

AB+AD+AD+DC+DC+CB+CB+AB >BD+ AC+DB+AC

2AB+2BC+2CD+2AD> 2AC + 2BD 

2(AB + BC + CD + AD) > 2(AC + BD)

    AB + BC + CD + AD > AC + BD

       P_ABCD > AC + BD (đpcm)