\(=n^2\left(n^4-n^2+2n+2\right)=\)

\(=n^2\left[n^2\left(n^2-1\right)+2\left(n+1\right)\right]=\)

\(=n^2\left[n^2\left(n-1\right)\left(n+1\right)+2\left(n+1\right)\right]=\)

\(=n^2\left[\left(n+1\right)\left(n^3-n^2+2\right)\right]=\)

\(=n^2\left\{\left(n+1\right)\left[\left(n^3+1\right)-\left(n^2-1\right)\right]\right\}=\)

\(=n^2\left\{\left(n+1\right)\left[\left(n^3+1\right)-\left(n-1\right)\left(n+1\right)\right]\right\}=\)

\(=n^2\left\{\left(n+1\right)\left[\left(n+1\right)\left(n^2-n+1\right)-\left(n-1\right)\left(n+1\right)\right]\right\}=\)

\(=n^2\left(n+1\right)^2\left(n^2-n+1\right)-n^2\left(n+1\right)^2\left(n-1\right)=\)

\(=n^2\left(n+1\right)^2\left[\left(n^2-n+1\right)-\left(n-1\right)\right]=\)

\(=n^2\left(n+1\right)^2\left(n^2-2n+2\right)\) Giả sử đây là số chính phương

\(\Rightarrow n^2-2n+2\) Phải là số chính phương

Ta có

\(n^2-2n+2=\left(n-1\right)^2+1\Rightarrow n^2-2n+2>\left(n-1\right)^2\) (1)

Ta có

\(n^2-2n+2=n^2-2\left(n-1\right)\) Với n>1

\(\Rightarrow n^2-2n+2< n^2\) (2)

Từ (1) và (2)

\(\Rightarrow\left(n-1\right)^2< n^2-2n+2< n^2\)

Mà \(\left(n-1\right)^2\) và \(n^2\) là hai số chính phương liên tiếp nên \(n^2-2n+2\) không phải là số chính phương

=> Biểu thức đề bài đã cho không phải là số chính phương

Kéo dài AB cắt Cy tại E và kéo dài CB cắt Ax tại G như hình vẽ dưới đây:

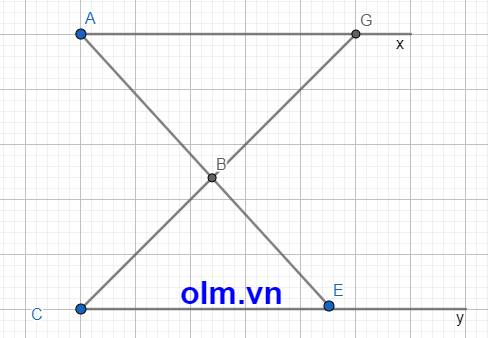
    \(\widehat{ABC}\) = \(\widehat{GBE}\)  (1) (vì đối đỉnh)

   \(\widehat{GBE}\) = \(\widehat{BCE}\) + \(\widehat{CEB}\) (2) ( vì góc ngoài của tam giác bằng tổng hai góc trong không kề với nó)

  \(\widehat{ABC}\)  = \(\widehat{GAB}\)     + \(\widehat{BCE}\) (3)

Từ (1); (2); (3) ta có: \(\widehat{BCE}\)  + \(\widehat{CEB}\) = \(\widehat{GAB}\) + \(\widehat{BCE}\) 

                        ⇒ \(\widehat{CEB}\) = \(\widehat{GAB}\)  

                         Mà hai  góc CEB và góc GAB là hai góc ở vị trí so le trong nên

                             Cy // Ax (đpcm)

\(a^3+b^3+c^3=3abc\)

\(\Rightarrow a^3+b^3+c^3-3abc=0\)

mà \(a^3+b^3+c^3-3abc=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)

\(\Rightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)=0\)

\(\Rightarrow a+b+c=0\)

\(\Rightarrow dpcm\)

\(A=x\left(x^2+x\right)+x\left(x+1\right)\)

\(A=x^2\left(x+1\right)+x\left(x+1\right)\)

\(A=\left(x+1\right)\left(x^2+x\right)\)

\(A=\left(x+1\right)x\left(x+1\right)\)

\(A=x\left(x+1\right)^2⋮\left(x+1\right)\)

\(\Rightarrow dpcm\)

Ta có: x^2 - 12x + 33 = (x^2 - 12x + 36) - 3 = (x - 6)^2 - 3.

Vậy hàm số y = x^2 - 12x + 33 có giá trị nhỏ nhất là -3, khi x = 6.

2. Sử dụng công thức tính đạo hàm:
Đạo hàm của hàm số y = x^2 - 12x + 33 là y' = 2x - 12.

Để tìm giá trị nhỏ nhất, ta giải phương trình y' = 0:
2x - 12 = 0
=> 2x = 12
=> x = 6.

Khi x = 6, ta có y = 6^2 - 12*6 + 33 = -3.

Vậy giá trị nhỏ nhất của hàm số y = x^2 - 12x + 33 là -3, khi x = 6.

\(A=x^2-12x+33\)

\(A=x^2-12x+36-3\)

\(A=\left(x-6\right)^2-3\)

mà \(\left(x-6\right)^2\ge0,\forall x\)

\(\Rightarrow A=\left(x-6\right)^2-3\ge0-3=-3\)

\(\Rightarrow GTNN\left(A\right)=-3\left(x=6\right)\)

\(\left(n-1\right)^2\left(n+1\right)+\left(n-1\right)\left(n+1\right)\)

\(=\left(n-1\right)\left(n+1\right)\left[\left(n-1\right)+1\right]\)

\(=\left(n-1\right)\left(n+1\right)\left(n-1+1\right)\)

\(=n\left(n-1\right)\left(n+1\right)\)

Xét: 

\(n\left(n-1\right)\) là hai số tự nhiên liên tiếp nên sẽ có số chẵn nên sẽ chia hết cho 2

\(n\left(n-1\right)\left(n+1\right)\) là 3 số tự nhiên liên tiếp nên sẽ chia hết cho 3

Mà: (2;3)=1 nên

\(n\left(n-1\right)\left(n+1\right)\) sẽ chia hết cho 2 x 3 =  6 (đpcm)

\(\left(n-1\right)^2\left(n+1\right)+\left(n-1\right)\left(n+1\right)\)

\(=\left(n-1\right)\left(n+1\right)\left(n-1+1\right)\)

\(=\left(n-1\right)n\left(n+1\right)\) là 3 số tự nhiên liên tiếp

\(\Rightarrow\left\{{}\begin{matrix}\left(n-1\right)n\left(n+1\right)⋮2\\\left(n-1\right)n\left(n+1\right)⋮3\end{matrix}\right.\)

\(\Rightarrow\left(n-1\right)n\left(n+1\right)⋮\left(2.3\right)\)

mà \(UCLN\left(2;3\right)=1\)

\(\Rightarrow\left(n-1\right)n\left(n+1\right)⋮6\)

\(\Rightarrow dpcm\)

\(A=n^4+2n^3+2n^2+n+7\)

\(\Rightarrow A=n^4+2n^3+n^2+n^2+n+7\)

\(\Rightarrow A=\left(n^2+n\right)^2+n^2+n+\dfrac{1}{4}+\dfrac{27}{4}\)

\(\Rightarrow A=\left(n^2+n\right)^2+\left(n+\dfrac{1}{2}\right)^2+\dfrac{27}{4}\)

\(\Rightarrow A>\left(n^2+n\right)^2\left(1\right)\)

Ta lại có :

\(\left(n^2+n+1\right)^2-A\)

\(=n^4+n^2+1+2n^3+2n^2+2n-n^4-2n^3-2n^2-n-7\)

\(=n^2+n-6\)

Để \(n^2+n-6>0\)

\(\Leftrightarrow\left(n+3\right)\left(n-2\right)>0\)

\(\Leftrightarrow\left[{}\begin{matrix}n< -3\\n>2\end{matrix}\right.\) \(\Rightarrow\left(n^2+n+1\right)^2>A\left(2\right)\)

\(\left(1\right),\left(2\right)\Rightarrow\left(n^2+n\right)^2< A< \left(n^2+n+1\right)^2\)

Nên A không phải là số chính phương

Xét \(-3\le n\le2\)

Để A là số chính phương

\(\Rightarrow n\in\left\{-3;-2;-1;0;1;2\right\}\)

Thay các giá trị n vào A ta thấy với \(n=-3;n=2\) ta đều được \(A=49\) là số chính phương

\(\Rightarrow\left[{}\begin{matrix}n=-3\\n=2\end{matrix}\right.\) thỏa mãn đề bài

 Bài toán tương đương với tìm số tự nhiên N có 4 chữ số sao cho N và \(N+1353\) đều là các SCP có 4 chữ số. Bạn chỉ cần đặt \(\left\{{}\begin{matrix}N=n^2\\N+1353=m^2\end{matrix}\right.\), trừ theo vế thu được \(\left(m-n\right)\left(m+n\right)=1353\). Tới đây bạn chặn \(0< m-n< m+n\) kèm theo \(32\le n\le92\) và \(49\le m\le99\) rồi chia trường hợp, đối chiếu điều kiện là xong.

 Ta có \(P=n^5-n=n\left(n^4-1\right)=n\left(n^2-1\right)\left(n^2+1\right)\)\(=n\left(n-1\right)\left(n+1\right)\left(n^2+1\right)\)

  Dễ thấy nếu \(5|n\), \(n\equiv1\left[5\right]\) hay \(n\equiv4\left[5\right]\) thì \(P⋮5\). Còn nếu \(n\equiv2\left[5\right]\) hay \(n\equiv3\left[5\right]\) thì \(n^2+1⋮5\Rightarrow P⋮5\). Vậy \(P=n^5-n⋮5,\) với mọi số tự nhiên \(n\). Suy ra \(D=P+2\equiv2\left[5\right]\)

 Mà một số chính phương khi chia cho 5 chỉ có thể dư 0, 1 hoặc 4 (chứng minh điều này rất dễ, bạn chỉ cần xét lần lượt \(n\equiv0,1,2,3,4\left[5\right]\) rồi đặt \(n=5k+i\left(0\le i\le4\right)\) rồi khai triển \(\left(5k+i\right)^2=25k+10ki+i^2\equiv i^2\left[5\right]\) là xong).

 Suy ra D không thể là số chính phương, nghĩa là không tồn tại n để D là số chính phương.

Gọi 2 số chính phương liên tiếp đó là \(n^2,\left(n+1\right)^2\). Ta có:

\(P=n^2+\left(n+1\right)^2+n^2\left(n+1\right)^2\)

\(=n^2+n^2+2n+1+n^2\left(n^2+2n+1\right)\)

\(=n^4+2n^3+3n^2+2n+1\)

Ta có \(\dfrac{P}{n^2}=n^2+2n+3+\dfrac{2}{n}+\dfrac{1}{n^2}\)

\(=\left(n+\dfrac{1}{n}\right)^2+2\left(n+\dfrac{1}{n}\right)+1\)

\(=\left(n+\dfrac{1}{n}+1\right)^2\)

\(\Rightarrow P=\left[n\left(n+\dfrac{1}{n}+1\right)\right]^2=\left(n^2+n+1\right)^2=\left[n\left(n+1\right)+1\right]^2\)

 Dễ dàng kiểm chứng được \(2|n\left(n+1\right)\), do đó \(n\left(n+1\right)+1\) là số lẻ, suy ra đpcm.

Hai số chính phương liên tiếp là \(n^2;\left(n+1\right)^2\)

Theo đề ta có :

\(n^2+\left(n+1\right)^2+n^2\left(n+1\right)^2\)

\(=n^2+n^2+2n+1+n^4+2n^3+n^2\)

\(=\left(n^4+n^3+n^2\right)+\left(n^3+n^2+n\right)+\left(n^2+n+1\right)\)

\(=n^2\left(n^2+n+1\right)+n\left(n^2+n+1\right)+\left(n^2+n+1\right)\)

\(=n^2\left(n^2+n+1\right)+n\left(n^2+n+1\right)+\left(n^2+n+1\right)\)

\(=\left(n^2+n+1\right)^2\)

\(=\left[n\left(n+1\right)+1\right]^2\)

mà \(n\left(n+1\right)⋮2\) (là 2 số tự nhiên liên tiếp)

\(\Rightarrow n\left(n+1\right)+1\) là số lẻ

\(\Rightarrow\left[n\left(n+1\right)+1\right]^2\) là số chính phương lẻ

\(\Rightarrow dpcm\)