a; A(\(x\)) = \(x^5\) - 2\(x^4\) + \(x^2\) - \(x\) + 1

   A(\(x\)) = \(x^5\) - 2\(x^4\) + \(x^2\) - \(x\) + 1

  B(\(x\)) = 6 - 2\(x\) - 3\(x^3\) + \(x^4\) - 3\(x^5\)

  B(\(x\)) = -3\(x^5\) + \(x^4\) - 3\(x^3\) - 2\(x\) + 6

b; A(\(x\)) + B(\(x\)) = \(x^5\) - 2\(x^4\) + \(x^2\) - \(x\) + 1 + \(x^4\) - 3\(x^5\) - 3\(x^3\) - 2\(x\) + 6

  A(\(x\)) + B(\(x\)) = (\(x^5\) - 3\(x^5\)) - (2\(x^4\) - \(x^4\)) - 3\(x^3\) + \(x^2\) - (\(x+2x\)) + (1+6)

 A(\(x\)) + B(\(x\)) = -2\(x^5\) - \(x^4\) - 3\(x^3\) + \(x^2\) - 3\(x\) + 7

a) Sắp xếp:

\(P\left(x\right)=2x^3+2x-3x^2+1=2x^3-3x^2+2x+1\)

\(Q\left(x\right)=2x^2+3x^2-x-5=5x^2-x-5\)

b) \(P\left(x\right)+Q\left(x\right)=\left(2x^3-3x^2+2x+1\right)+\left(5x^2-x-5\right)\)

\(=2x^3+\left(-3x^2+5x^2\right)+\left(2x-x\right)+\left(1-5\right)\)

\(=2x^3+2x^2+x-4\)

c) \(P\left(x\right)-Q\left(x\right)=\left(2x^3-3x^2+2x+1\right)-\left(5x^2-x-5\right)\)

\(=2x^3+\left(-3x^2-5x^2\right)+\left(2x+x\right)+\left(1+5\right)\)

\(=2x^3-7x^2+3x+4\)

nha bạn

a; A(\(x\)) = 5\(x\) - \(x^3\) - 15 + 4\(x^2\) 

   A(\(x\)) = - \(x^3\) + 4\(x^2\) - 5\(x\) - 15

 B(\(x\)) = 4\(x^2\) + 2\(x^3\) + 5\(x\) + 17 

B(\(x\)) = 2\(x^3\) + 4\(x^2\) + 5\(x\) + 17

a) Sắp xếp:

\(A\left(x\right)=5x-x^3-15+4x^2=-x^3+4x^2+5x-15\)

\(B\left(x\right)=4x^2+2x^3+17+5x=2x^3+4x^2+5x+17\)

b) \(A\left(x\right)+B\left(x\right)=\left(-x^3+4x^2+5x-15\right)+\left(2x^3+4x^2+5x+17\right)\)

\(=\left(-x^3+2x^3\right)+\left(4x^2+4x^2\right)+\left(5x+5x\right)+\left(-15+17\right)\)

\(=x^3+8x^2+10x+2\) 

\(A\left(x\right)-B\left(x\right)=\left(-x^3+4x^2+5x-15\right)-\left(2x^3+4x^3+5x+17\right)\)

\(=\left(-x^3-2x^3\right)+\left(4x^2-4x^2\right)+\left(5x-5x\right)+\left(-15-17\right)\)

\(=-3x^3-32\)

\(\dfrac{x^2}{y}=3\) và \(\dfrac{x}{y}=21\) \(\left(ĐKXĐ:x,y>0\right)\)

\(\Rightarrow\dfrac{x^2}{y}:\dfrac{x}{y}=\dfrac{3}{21}=\dfrac{1}{7}\)

\(\Rightarrow\dfrac{x^2}{y}\cdot\dfrac{y}{x}=\dfrac{1}{7}\)

\(\Rightarrow x=\dfrac{1}{7}.\)

Khi đó: \(y=\dfrac{x}{21}=\dfrac{1}{7}:21=\dfrac{1}{7}\cdot\dfrac{1}{21}=\dfrac{1}{147}\)

\(\Rightarrow y=\dfrac{1}{147}\)

Vậy \(\left(x;y\right)=\left(\dfrac{1}{7};\dfrac{1}{147}\right)\)

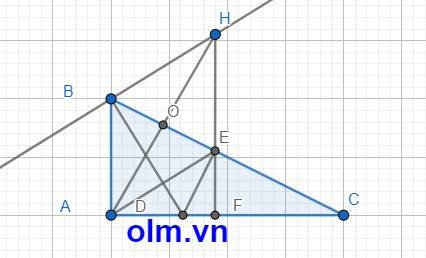
a; Xét tam giác vuông ABD và tam giác vuông  EBD có

\(\widehat{ABD}\) = \(\widehat{EBD}\) (vì BD là phân giác của góc B)

Cạnh BD chung

⇒\(\Delta\)ABD = \(\Delta\)EBD (cạnh huyền góc nhọn)

⇒ BA = BE (đpcm)

b; BA = BE (cmt)

   ⇒\(\Delta\)ABE cân tại B

    BD là phân giác góc ABE

    ⇒ BD là đường trung trực của AE vì trong tam giác đường phân giác cũng là đường trung trực)

c; BD \(\perp\)BH (gt)

    BD \(\perp\)AE (cmt)

⇒ BH//AE (vì hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau)

Xét tứ giác ABHE có

    BH//AE (cmt)

    BH = AE (gt)

⇒ Tứ giác ABHE là hbh (vì tứ giác có một cặp cạnh đối diện song song và bằng nhau thì tứ giác đó là hình hình bình hành)

⇒ AB//HE 

  ⇒ AC \(\perp\) HE (Vì một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.)

  d; Tứ giác ABHE là hình bình hành 

       O là trung điểm BE 

      ⇒ O là trung điểm của AH

     Vì hình bình hành có hai đường chéo cắt nhau tại trung điểm mỗi đường.

      ⇒ A; O; H thẳng hàng (đpcm)

ai đó trả lời có được không?

   Hệ số và bậc của đơn thức 5\(x^4\) lần lượt là: 5 và 4 

Hệ số của đơn thức \(5x^4\) là: 5 

Bậc của đơn thức \(5x^4\) là: \(4\)

⇒ Chọn A

Bài 1: Thực hiện phép tính:

a; (\(\dfrac{9}{25}\) - 2.18): (3\(\dfrac{4}{5}\) + 0,2)

 =   (0,36 - 36): (3,8 + 0,2)

 =   - 35,64 : 4

= -  8,91

b; \(\dfrac{3}{8}\).19.\(\dfrac{1}{3}\)  - \(\dfrac{3}{8}\).33.\(\dfrac{1}{3}\)

= \(\dfrac{3}{8}\).(19\(\dfrac{1}{3}\) - 33\(\dfrac{1}{3}\))

= \(\dfrac{3}{8}\).(19 + \(\dfrac{1}{3}\) - 33 - \(\dfrac{1}{3}\))

= \(\dfrac{3}{8}\).(-14)

= - \(\dfrac{21}{4}\)

a) Do AD là tia phân giác của ∠BAC (gt)

⇒ ∠BAD = ∠CAD

Do ∆ABC cân tại A (gt)

⇒ AB = AC

Xét ∆ABD và ∆ACD có:

AB = AC (cmt)

∠BAD = ∠CAD (cmt)

AD là cạnh chung

⇒ ∆ABD = ∆ACD (c-g-c)

b) Do ∆ABD = ∆ACD (cmt)

⇒ ∠ADB = ∠ADC (hai góc tương ứng)

Mà ∠ADB + ∠ADC = 180⁰ (kề bù)

⇒ ∠ADB = ∠ADC = 180⁰ : 2 = 90⁰

⇒ AD ⊥ BC (1)

Do ∆ABD = ∆ACD (cmt)

⇒ BD = CD (hai cạnh tương ứng)

⇒ D là trung điểm của BC (2)

Từ (1) và (2) ⇒ AD là đường trung trực của BC

c) Do ∠BAD = ∠CAD (cmt)

⇒ ∠MAD = ∠NAD

Xét ∆ADM và ∆ADN có:

AD là cạnh chung

∠MAD = ∠NAD (cmt)

AM = AN (gt)

⇒ ∆ADM = ∆ADN (c-g-c)