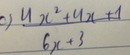
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(ax+by+cz=0\)
\(\Rightarrow\left(ax+by+cz\right)^2=0\)
\(\Rightarrow a^2x^2+b^2y^2+c^2z^2+2\left(axby+bycz+axcz\right)=0\)
\(\Rightarrow a^2x^2+b^2y^2+c^2z^2=-2\left(axby+bycz+axcz\right)\)
Lại có: \(\frac{ax^2+by^2+cz^2}{bc\left(y-z\right)^2+ac\left(x-z\right)^2+ab\left(x-y\right)^2}\)
\(=\frac{ax^2+by^2+cz^2}{bc\left(y^2-2yz+z^2\right)+ac\left(x^2-2xz+z^2\right)+ab\left(x^2-2xy+y^2\right)}\)
\(=\frac{ax^2+by^2+cz^2}{bcy^2-2bcyz+bcz^2+acx^2-2acxz+acz^2+abx^2-2abxy+aby^2}\)
\(=\frac{ax^2+by^2+cz^2}{bcy^2+bcz^2+acx^2+acz^2+abx^2+aby^2-2\left(bcyz+acxz+abxy\right)}\)
\(=\frac{ax^2+by^2+cz^2}{bcy^2+bcz^2+acx^2+acz^2+abx^2+aby^2+a^2x^2+b^2y^2+c^2z^2}\)
\(=\frac{ax^2+by^2+cz^2}{\left(acx^2+abx^2+a^2x^2\right)+\left(bcy^2+aby^2+b^2y^2\right)+\left(bcz^2+acz^2+c^2z^2\right)}\)
\(=\frac{ax^2+by^2+cz^2}{ax^2\left(c+b+a\right)+by^2\left(c+a+b\right)+cz^2\left(b+a+c\right)}\)
\(=\frac{ax^2+by^2+cz^2}{\left(a+b+c\right)\left(ax^2+by^2+cz^2\right)}=\frac{1}{a+b+c}=\frac{1}{\frac{1}{2020}}=2020\) (đpcm)

Bai lam
\(\frac{4x^2+4x+1}{6x+3}=\frac{\left(2x+1\right)^2}{3\left(2x+1\right)}=\frac{2x+1}{3}\)
Hoc tot

\(VT=\left(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{2k}\right)-2\left(\frac{1}{2}+\frac{1}{4}+..+\frac{1}{2k}\right)\)
\(=\left(1+\frac{1}{2}+\frac{1}{3}+..+\frac{1}{k}\right)+\left(\frac{1}{k+1}+\frac{1}{k+2}+..+\frac{1}{2k}\right)-\left(1+\frac{1}{2}+...+\frac{1}{k}\right)=VP\)
có dpcm

a) Phương trình hoá học của phản ứng :
2Al+3H2SO4→Al2(SO4)3+3H22Al + 3{H_2}S{O_4} \to A{l_2}{(S{O_4})_3} + 3{H_2}2Al+3H2SO4→Al2(SO4)3+3H2
Phương trình hoá học cho biết : cứ 2 nguyên tử AI tác dụng với 3 phân tưH2SO4, tạo ra 1 phân tử Al2(SO4)3 và 3 phân tử H2.
b) Nếu có 6,02.1023 nguyên tử AI sẽ tác dụng với 6,02.1023×32(=9,03×1023)6,{02.10^{23}} \times {3 \over 2}( = 9,03 \times {10^{23}})6,02.1023×23(=9,03×1023)
phân tử H2SO4, tạo ra 6,02.1023×12(=3,01×1023)6,{02.10^{23}} \times {1 \over 2}( = 3,01 \times {10^{23}})6,02.1023×21(=3,01×1023) phân tử Al2(SO4)3và
6,02.1023×32(=9.03×1023)6,{02.10^{23}} \times {3 \over 2}( = 9.03 \times {10^{23}})6,02.1023×23(=9.03×1023) phân tử H2.
c) Đáp số : 4,515.1023 phân tử H2SO4
1,505.1023 phân tử Al2(SO4)3
4,515.1023 phân tử H2

Quặng malachit có thành phần chính là hai hợp chất của đồng được ghi bằng công thức chung là Cu2(OH)2CO3. Khi nung nóng thì hai hợp chất này bị phân huỷ, sản phẩm của phản ứng phân huỷ gồm có CuO, H2O và CO2.
a)Viết phương trình hoá học của phản ứng phân huỷ mỗi hợp chất của đồng.
b)Biết rằng khi nung nóng 4,8 kg quặng thì thu được 3,2 kg CuO cùng với 0,36 kg nước và 0,88 kg CO2. Tính tỉ lệ phần trăm về khối lượng hai hợp chất của đồng có chứa trong quặng.
Giải
a) Công thức hóa học hai hợp chất của đồng:
(C{u_2}{(OH)_2}C{O_3} o Cu{(OH)_2}vàCuC{O_3})
Các phương trình hóa học của phản ứng phân hủy:
(Cu{(OH)_2} o CuO + {H_2}O)
(CuC{O_3} o CuO + C{O_2})
b) Theo định luật bảo toàn khối lượng, khới lượng hai hợp chất của đồng đã phân hủy bằng:
({m_{Cu}}_{_2{{(OH)}_2}C{O_3}} = {m_{CuO}} + {m_{{H_2}O}} + {m_{C{O_2}}} = 3,2 + 0,36 + 0,88 = 4,44(kg))
Tỷ lệ phần trăm về khối lượng hai hợp chất của đồng có chứa trong quặng bằng:
({m_{Cu}}_{_2{{(OH)}_2}C{O_3}} = {{4,44} over {4,8}} imes 100\% = 92,5\% ) .


\(\left(x^2+x\right)\left(x^2+x+1\right)=6\)
Đặt x^2 + x = t
\(t\left(t+1\right)=6\Leftrightarrow t^2+t=6\)
\(\Leftrightarrow t^2+t-6=0\Leftrightarrow t^2+3t-2t-6=0\)
\(\Leftrightarrow\left(t-2\right)\left(t+3\right)=0\Leftrightarrow t=2;-3\)
Sr tưởng giải PT
\(\left(x^2+x\right)\left(x^2+x+x\right)=6\)
\(\Leftrightarrow x^4+x^3+x^2+x^3+x^2+x=6\)
\(\Leftrightarrow x^4+2x^3+2x^2+x=6\)
\(\Leftrightarrow x^4+2x^3+2x^2+x-6=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x^2+x+3\ne0\right)=0\Leftrightarrow x=1;-2\)
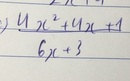
Bài làm
\(\frac{4x^2+4x+1}{6x+3}=\frac{\left(2x+1\right)^2}{3\left(2x+1\right)}=\frac{2x+1}{3}\)
Học tốt