Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(\left\{{}\begin{matrix}\left|x-3\right|\ge0\forall x\\\left|y+3\right|\ge0\forall y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(\left|x-3\right|+2\right)^2\ge2^2=4\forall x\\\left|y+3\right|\ge0\forall y\end{matrix}\right.\)
\(\Rightarrow\left(\left|x-3\right|+2\right)^2+\left|y+3\right|\ge4\forall x,y\)
\(\Rightarrow P=\left(\left|x-3\right|+2\right)^2+\left|y+3\right|+2018\ge4+2018=2022\forall x,y\)
Dấu \("="\) xảy ra khi: \(\left\{{}\begin{matrix}x-3=0\\y+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-3\end{matrix}\right.\)
Vậy \(Min_P=2022\) khi \(x=3;y=-3\).

\(\Leftrightarrow36x-20=4y^2-4y\)
\(\Leftrightarrow18\left(2x-1\right)=\left(2y-1\right)^2+1\)
Vế trái chia hết cho 3, vế phải chia 3 luôn dư 1 hoặc 2
Vậy không tồn tại cặp số nguyên x, y thỏa mãn
Vì \(9x-5\equiv4\left[9\right]\) nên \(y\left(y-1\right)=y^2-y\equiv4\left[9\right]\) hay \(y^2-y-4⋮9\)
\(\Leftrightarrow y^2-5y+4y-20+16⋮9\)
\(\Leftrightarrow\left(y-5\right)\left(y+4\right)+16⋮9\)
\(\Leftrightarrow\left(y-5\right)\left(y+4\right)-2⋮9\)
\(\Leftrightarrow\left(y-5\right)\left(y-5+9\right)-2⋮9\)
\(\Leftrightarrow\left(y-5\right)^2+9\left(y-5\right)-2⋮9\)
\(\Leftrightarrow\left(y-5\right)^2-2⋮9\)
\(\Rightarrow\left(y-5\right)^2-2⋮3\) hay \(\left(y-5\right)^2\equiv2\left(mod3\right)\)
Điều này là vô lí vì số chính phương khi chia cho 3 không thể có số dư là 2.
Vậy pt đã cho không có nghiệm nguyên.

Bài 3.4
a; \(\dfrac{36}{84}\) = \(\dfrac{42}{98}\)
\(\dfrac{36}{84}\) = \(\dfrac{36:12}{84:12}\) = \(\dfrac{3}{7}\)
\(\dfrac{42}{98}\) = \(\dfrac{42:14}{98:14}\) = \(\dfrac{3}{7}\)
Vậy \(\dfrac{36}{84}\) = \(\dfrac{42}{98}\) (đpcm)
b; \(\dfrac{123}{237}\) = \(\dfrac{123123}{237237}\)
\(\dfrac{123123}{237237}\) = \(\dfrac{123123:1001}{237237:1001}\) = \(\dfrac{123}{237}\) (đpcm)

Gấp rưỡi là gấp \(\dfrac{3}{2}\)
Tuổi anh bằng \(\dfrac{3}{2}\) tuổi em
Hiệu số tuổi hai anh em luôn không đổi theo thời gian.
Tuổi anh hiện nay bằng: 3 : (3 - 2) = \(\dfrac{3}{1}\) (hiệu số tuổi hai anh em)
Tuổi anh bảy năm trước bằng: 2 : (2-1) = \(\dfrac{2}{1}\) (hiệu số tuổi hai anh em)
7 tuổi ứng với: \(\dfrac{3}{1}\) - \(\dfrac{2}{1}\) = \(\dfrac{1}{1}\) (hiệu số tuổi hai anh em)
Hiệu số tuổi hai anh em là:
7 : \(\dfrac{1}{1}\) = 7 (tuổi)
Tuổi anh hiện nay là:
7 x \(\dfrac{3}{1}\) = 21 (tuổi)
Đáp số:...

(6\(xy\) - 10) + (3y - 12) = 12
6\(xy\) - 10 + 3y - 12 = 12
6\(xy\) + 3y = 12 + 12 + 10
y.(6\(x\) + 3) = 34
34 = 2.17
Ư(34) = {-34; -17; -2; -1; 1; 2; 17; 34}
Lập bảng ta có:
| y | -34 | -17 | -2 | -1 | 1 | 2 | 17 | 34 |
| 6\(x\)+ 3 | -1 | -2 | -17 | -34 | 34 | 17 | 2 | 1 |
| \(x\) | -\(\dfrac{2}{3}\) | -\(\dfrac{5}{3}\) | -\(\dfrac{10}{3}\) | -\(\dfrac{37}{6}\) | \(\dfrac{31}{6}\) | \(\dfrac{7}{3}\) | -\(\dfrac{1}{6}\) | \(-\dfrac{1}{3}\) |
Theo bảng trên ta có không có cặp giá trị nguyên nào của \(x\); y thỏa mãn đề bài.

\(a^2+c^2=b^2+d^2\)
\(\Leftrightarrow a^2+b^2+c^2+d^2=2\left(b^2+d^2\right)⋮2\)
Ta có
\(a^2+b^2+c^2+d^2+\left(a+b+c+d\right)=\)
\(=a\left(a+1\right)+b\left(b+1\right)+c\left(c+1\right)+d\left(d+1\right)\)
Ta thấy
\(a\left(a+1\right);b\left(b+1\right);c\left(c+1\right);d\left(d+1\right)\) là tích của 2 số TN liên tiếp nên chúng chia hết cho 2
\(\Rightarrow a^2+b^2+c^2+d^2+\left(a+b+c+d\right)⋮2\)
Mà \(a^2+b^2+c^2+d^2⋮2\left(cmt\right)\)
\(\Rightarrow a+b+c+d⋮2\)
Mà a+b+c+d là các số TN khác 0 => a+b+c+d>2
=> a+b+c+d là hợp số
A = [(a +b) + (c + d)].[(a + b) + (c + d)]
A = (a + b).(a + b) + (a +b).(c + d) + (c + d).(a + b) + (c+d).(c+d)
A = a2 + ab + ab + b2 + 2.(a+b).(c+d) + c2 + cd + cd + d2
A = a2 + b2 + c2 + d2 + 2ab + 2.(a +b).(c + d) + 2cd
A = a2 + b2 + a2 + b2 + 2. [ab + (a + b).(c + d) + cd]
A = 2.(a2 + b2) + 2.[ab + (a + b)(c + d) + cd]
⇒ A ⋮ 2 ⇒ a + b + c + d ⋮ 2 mà a; b;c;d là số tự nhiên nên a + b + c + d > 2
Hay A ⋮ 1; 2; A vậy A là hợp số (đpcm)

Lượng cùi dừa dùng: 600:3 x2 = 400 (gam)
Lượng đường cần dùng: 400 : 20 = 20 (gam)
Đs:......
Lượng cùi dừa dùng là
600:3 x2 = 400 (g)
Lượng đường cần dùng là
400 : 20 = 20 (g)

\(\dfrac{12}{16}\) < \(\dfrac{16}{◻}\) < \(\dfrac{12}{15}\)
\(\dfrac{12\times4}{16\times4}\) < \(\dfrac{16\times3}{◻\times3}\) < \(\dfrac{12\times4}{15\times4}\)
\(\dfrac{48}{64}\) < \(\dfrac{48}{◻\times3}\) < \(\dfrac{48}{60}\)
64 > \(◻\) \(\times\) 3 > 60
\(\dfrac{64}{3}\) > \(◻\) > \(\dfrac{60}{3}\)
\(\dfrac{64}{3}\) > \(◻\) > 20
\(◻\) = 19

\(\dfrac{8}{14}\) < \(\dfrac{◻}{19}\) < \(\dfrac{9}{14}\)
\(\dfrac{8\times19}{14\times19}\) < \(\dfrac{◻\times14}{14\times19}\) < \(\dfrac{9\times19}{14\times19}\)
8\(\times\)19 < \(◻\) \(\times\) 14 < 9\(\times\)19
152 < \(◻\) \(\times\) 14 < 171
\(\dfrac{152}{14}\) < \(◻\) < \(\dfrac{171}{14}\)
\(◻\) = 11; 12
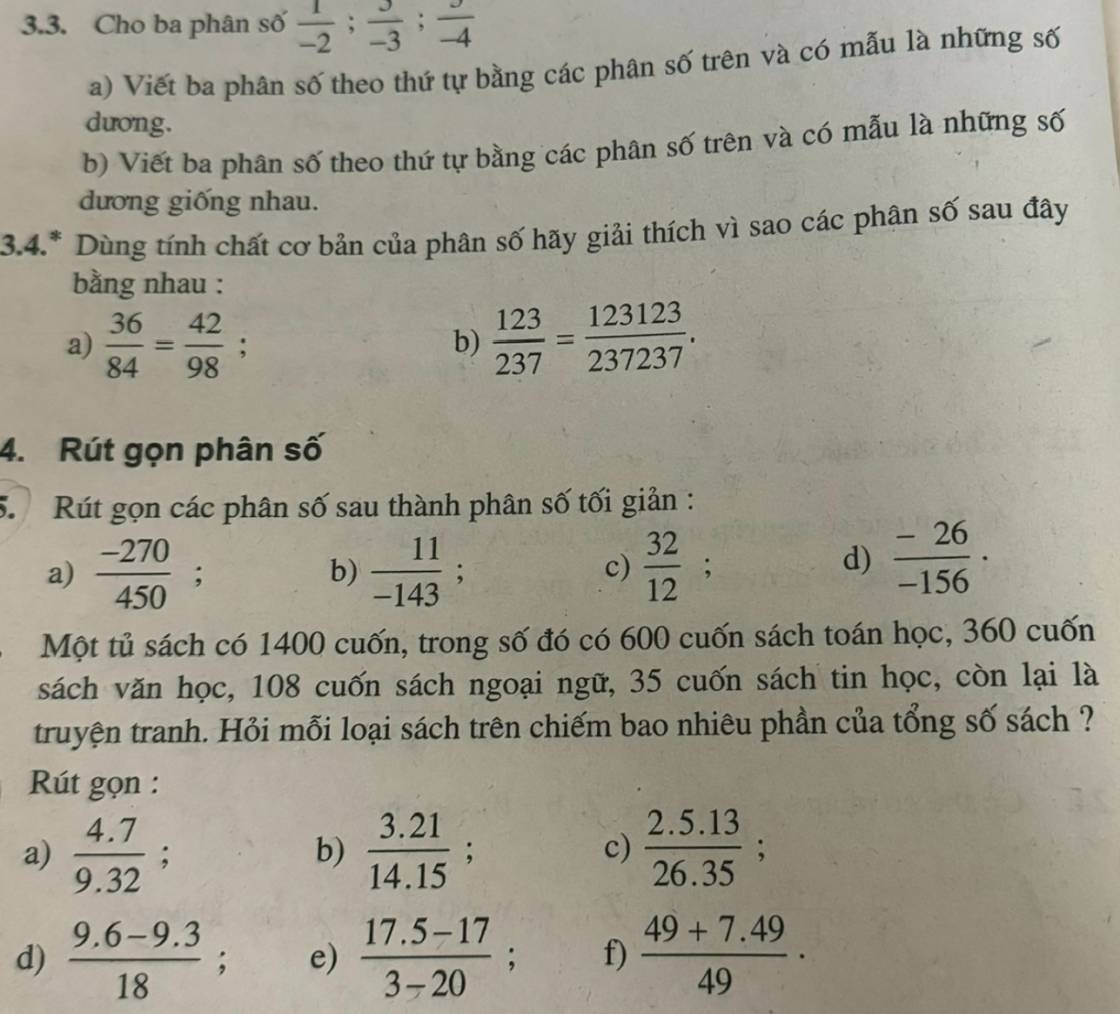
Do số thứ nhất (a) = 40% tổng của 2 số ⇒ số thứ hai (b) = 60% tổng của 2 số.
a = 40% (a + b)
a + b = 100% (a + b)
⇒ b = 60% (a + b)
⇒ \(\dfrac{a}{b}=\dfrac{40}{60}=\dfrac{2}{3}\)
Số thứ nhất là: 42,5 : (3 - 2) x 2 = 85
Số thứ 2 là: 85 + 42,5 = 127,5
Đáp số: Số thứ nhất: 85
Số thứ hai: 127,5
Do số thứ nhất (a) = 40% tổng của 2 số ⇒ số thứ hai (b) = 60% tổng của 2 số.
a = 40% (a + b)
a + b = 100% (a + b)
⇒ b = 60% (a + b)
⇒ ��=4060=23ba=6040=32
Số thứ nhất là: 42,5 : (3 - 2) x 2 = 85
Số thứ 2 là: 85 + 42,5 = 127,5
Đáp số: Số thứ nhất: 85
Số thứ hai: 127,5