110x(193+2023)+110x(-2023)+193x90
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đổi: \(\dfrac{4}{5}m=8dm\)
Diện tích tam giác là:
\(\left(8\times3,5\right):2=14\left(dm^2\right)\)
Đáp số: ...
\(\dfrac{4}{5}\)m = \(8\) dm
Diện tích tam giác đó là:
8 x 3,5 : 2 = 14 (dm2)
Đáp số...

12 giây x 50 = 600 giây = 10 phút
9 phút 45 giây < 10 phút
Vậy 12 giây x 50 > 9 phút 45 giây
12 giây x 50 = 600 giây
9 phút 45 giây = 585 giây
Vì 600 > 585
=> 12 giây x 50 > 9 phút 45 giây


60 phút x 60 = 3600 phút = 60 giờ.
⇒ 15 giờ < 60 giờ.
⇒ 15 giờ < 60 phút x 60.
15 giờ = 900 phút
60 phút x 60 = 3600 phút
Vì 900 < 3600
=> 15 giờ < 60 phút x 60

\(\left(2x+4\right)^{2024}+\left(\left|3y-9\right|\right)^{2023}=0\) (*)
Ta có: \(\left(2x+4\right)^{2024}\ge0\forall x\) (vì có số mũ chẵn) (1)
\(\left(\left|3y-9\right|\right)^{2023}\ge0\forall y\) (vì giá trị tuyệt đối luôn ≥0) (2)
Từ (1) và (2) ta có:
\(\Rightarrow\left\{{}\begin{matrix}2x+4=0\\3y-9=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-2\\y=3\end{matrix}\right.\)
Vậy: ...

Số bé nhất có 4 chữ số khác nhau lớn hơn 5000 là: 5012

\(A=\dfrac{10n-3}{5n+2}=\dfrac{10n+4-7}{5n+2}=\dfrac{2\left(5n+2\right)-7}{5n+2}=2-\dfrac{7}{5n+2}\)
Để A nguyên thì \(7\) ⋮ 5n + 2
\(\Rightarrow5n+2\inƯ\left(7\right)=\left\{1;-1;7;-7\right\}\)
\(\Rightarrow5n\in\left\{-1;-3;5;-9\right\}\)
\(\Rightarrow n\in\left\{-\dfrac{1}{5};-\dfrac{3}{5};1;-\dfrac{9}{5}\right\}\)
________________
\(B=\dfrac{12n+5}{6n-3}=\dfrac{12n-6+11}{6n-3}=\dfrac{2\left(6n-3\right)+11}{6n-3}=2+\dfrac{11}{6n-3}\)
Để B nguyên thì \(11\) ⋮ 6n - 3
\(\Rightarrow6n-3\inƯ\left(11\right)=\left\{1;-1;11;-11\right\}\)
\(\Rightarrow6n\in\left\{4;2;14;-8\right\}\)
\(\Rightarrow n\in\left\{\dfrac{2}{3};\dfrac{1}{3};\dfrac{7}{3};-\dfrac{4}{3}\right\}\)

Tổng giá tiền của 5 quyển vở và 5 cái bút là:
200 000 - 50 000 - 10 000 = 140 000 (đồng)
Tổng giá tiền của 1 quyển vở và 1 cái bút là:
140 000 : 5 = 28 000 (đồng)
Giá tiền của một cái bút là:
(28 000 + 12 000):2 = 20 000 (đồng)
Giá tiền của một quyển vở là:
20 000 - 12 000 = 8 000 (đồng)

Ta có:
\(VT=\left|2x+3\right|+\left|1-2x\right|\ge\left|2x+3+1-2x\right|=4\)
Mặt khác do \(\left(x+1\right)^2\ge0;\forall x\) nên:
\(VP=\dfrac{8}{3\left(x+1\right)^2+2}\le\dfrac{8}{3.0+2}=4\)
\(\Rightarrow VT\ge VP\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}\left(2x+3\right)\left(1-2x\right)\ge0\\\left(x+1\right)^2=0\end{matrix}\right.\)
\(\Rightarrow x=-1\)
Ta có VT: \(\left|2x+3\right|+\left|2x-1\right|=\left|2x+3\right|+\left|1-2x\right|\)
Áp dụng bđt: \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\)
\(\Rightarrow\left|2x+3\right|+\left|1-2x\right|\ge\left|2x+3+1-2x\right|=4\) (1)
VP: \(\dfrac{8}{3\left(x+1\right)^2+2}\le\dfrac{8}{3\cdot0+2}=\dfrac{8}{2}=4\) (2)
Từ (1) và (2) để 2 vế bằng nhau thì:
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}x+1=0\\\left(2x+3\right)\left(1-2x\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-1\\-\dfrac{3}{2}\le x\le\dfrac{1}{2}\end{matrix}\right.\)
Vậy x = -1 giá trị thỏa mãn
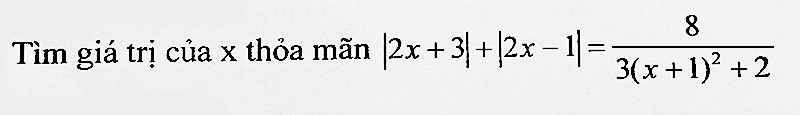
110 x (193 + 2023) + 110 x (-2023) + 193 x 90
= 110 x (193 + 2023 - 2023) + 193 x 90
= 110 x 193 + 193 x 90
= 193 x (110 + 90)
= 193 x 200
= 38600
110 x (193 + 2023) + 110 x (-2023) + 193 x 90
= 110 x (193 + 2023 + (-2023) + 193 x 90
= 110 x 193 + 193 x 90
= 193 x (110 + 90)
= 193 x 200
= 193 x 100 x 2
= 19300 x 2
= 38600