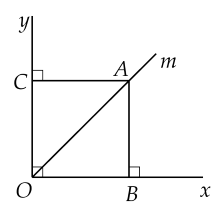
Cho $\widehat{xOy}={{90}^{\circ}}$ và tia phân giác $Om$. Lấy điểm $A$ trên $Om.$ Kẻ $AB, \, AC$ lần lượt vuông góc với $Ox, \, Oy\,.$ Chứng minh $OBAC$ là hình vuông.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
|x - 1| + |x - 7|
= |x - 1| + |7 - x|
≥ |x - 1 + 7 - x| = 6
Vậy |x + 1| + |x - 7| ≥ 6

`B=y^2-4y+5`
`=y^2-4y+4+1`
`=(y-2)^2+1`
với `y=12` ta có
`(12-2)^2+1=10^2+1=100+1=101`
Với y=12, ta có
12² - 4x12 + 5
= 144 - 48 + 5
= 96 + 5=101

Góc DAC là góc nằm trong tam giác ABD, nên ta có thể tính được bằng cách lấy tổng các góc trong tam giác ABD trừ đi góc ADB: Góc DAC = 180° - góc ABD = 180° - 60° = 120°
Góc ADB là góc nằm trong tam giác CBD, nên ta có thể tính được bằng cách lấy tổng các góc trong tam giác CBD trừ đi góc CDB:
Góc ADB = 180° - góc CBD = 180° - 20° = 160°
Vậy số đo các góc DAC và ADB lần lượt là 120° và 160°.

Nếu m hoặc n chia hết cho 3 thì hiển nhiên \(nm\left(m^2-n^2\right)⋮3\)
Nếu cả m và n đều không chia hết cho 3 thì \(m^2,n^2\) đều chia 3 dư 1 (tính chất của số chính phương). Do đó \(m^2-n^2⋮3\) nên \(mn\left(m^2-n^2\right)⋮3\)
Vậy \(mn\left(m^2-n^2\right)⋮3\) với mọi cặp số nguyên m, n.

\(B=3x^2-2x+7\\ =3\left(x^2-\dfrac{2}{3}x+\dfrac{1}{9}\right)+\dfrac{20}{3}\\ =3\left(x-\dfrac{1}{3}\right)^2+\dfrac{20}{3}\\ Vì:\left(x-\dfrac{1}{3}\right)^2\ge0\Rightarrow3\left(x-\dfrac{1}{3}\right)^2\ge0\forall x\in R\\ Vậy:min_B=\dfrac{20}{3}khi.\left(x-\dfrac{1}{3}\right)=0\Leftrightarrow x=\dfrac{1}{3}\)

a/
\(\left(x+y\right)^2=x^2+y^2+2xy=\left(-2\right)^2\)
\(\Leftrightarrow x^2+y^2-2.35=4\Leftrightarrow x^2+y^2=74\)
\(\Rightarrow\left(x^2+y^2\right)^2=x^4+y^4+2x^2y^2=74^2\)
\(\Rightarrow x^4+y^4=74^2-2.\left(-35\right)^2\)
b/
\(\left(x^4+y^4\right)\left(x+y\right)=x^5+x^4y+xy^4+y^5\)
\(\Leftrightarrow x^5+y^5=\left(x^4+y^4\right)\left(x+y\right)-xy\left(x^3+y^3\right)\)(1)
Ta có
\(x^3+y^3=\left(x+y\right)\left(x^2-xy+y^2\right)\)
Thay các giá trị đã tính được vào (1) Bạn tự tính nốt nhé
Bạn thấy số giúp mình đc ko tại mình hơi yếu phần này


\(AC\perp Oy\) (gt); \(Ox\perp Oy\) (gt) => AC//Oy => AC//OB
C/m tương tự có AB//OC
=> OBAC là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Mà \(\widehat{xOy}=90^o\)
=> OBAC là HCN
Ta có
AC=AB (Tính chất đường phân giác)
=> OBAC là hình vuông
Tứ giác ����OBAC có ba góc vuông: góc B= góc C = góc BOC= 90 độ �^=�^=���^=90∘==
∘
Nên ����OBAC là hình chữ nhật.
Mà �A nằm trên tia phân giác ��OM suy ra ��=��AB=AC.
Khi đó ����OBAC là hình vuông.